Hàng đ iợ
•C u trúc d li u ho t đ ng theo c ch ấ ữ ệ ạ ộ ơ ế first-in
first-out (FIFO)
•Hai thao tác c b n:ơ ả
–Chèn vào hàng đ i: ợenqueue
–L y ra kh i hàng đ i: ấ ỏ ợ dequeue
•Các đ i t ng trong hàng đ i đ c s p th t ố ượ ợ ượ ắ ứ ự
theo th i gian chúng đ c chèn vào hàngờ ượ
•Đ i t ng đ c l y ra kh i hàng đ i là đ i t ng ố ượ ượ ấ ỏ ợ ố ượ
đ c chèn vào tr c nh tượ ướ ấ
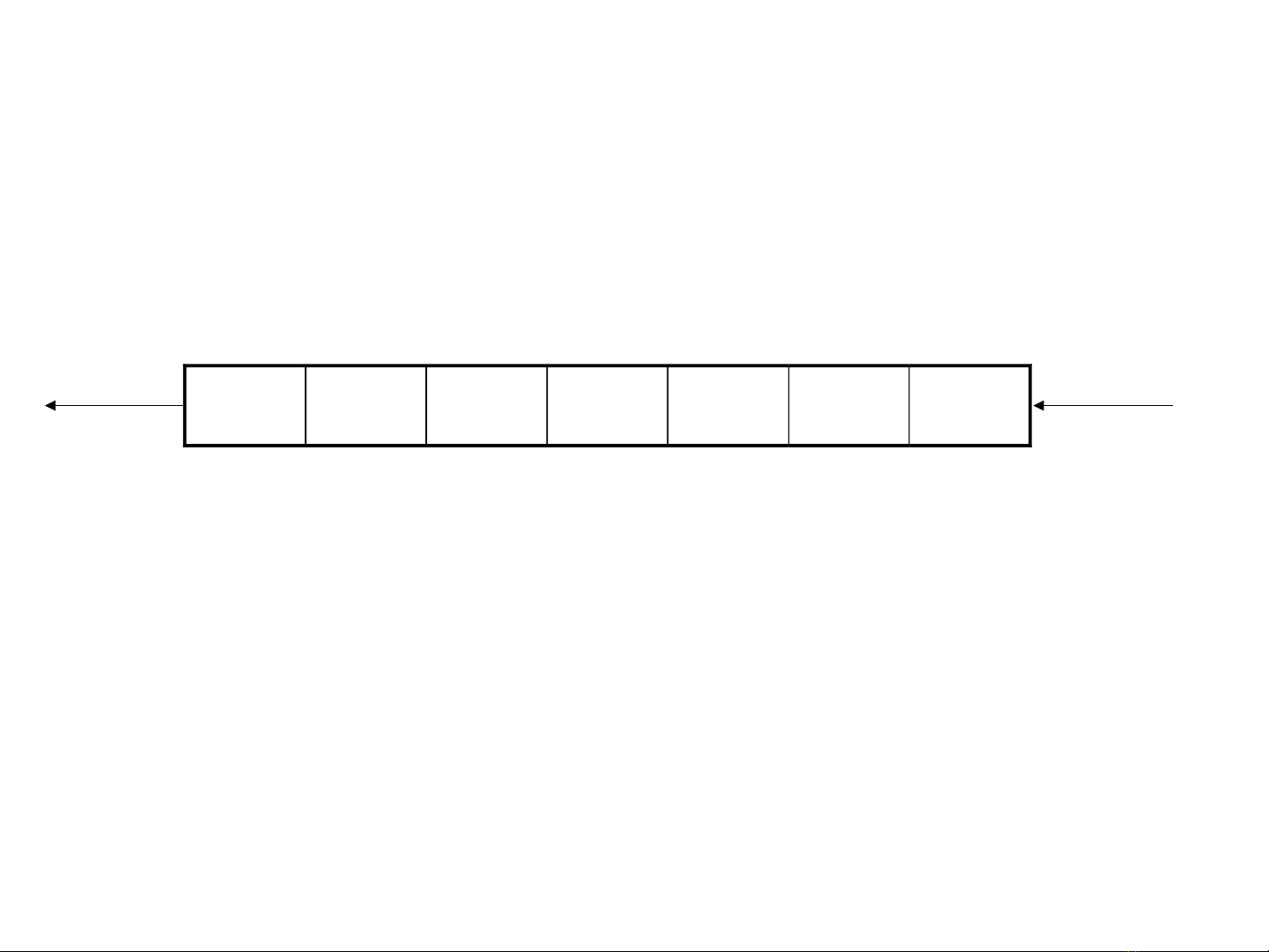
Hàng đ iợ
A B C D ... M N
head of queue tail of queue
enqueuedequeue
Hàng đ i, s d ng m ngợ ử ụ ả
Khai báo c u trúc hàng đ iấ ợ
Typerdef struct Queue
{
int *arrQueue;
int max;
int numItems;
int front;
int rear;
}
Hàng đ i, s d ng m ngợ ử ụ ả
Thao tác kh i t o hàng đ i r ngở ạ ợ ỗ
int InitQueue(Queue &q, int maxItems)
{
q.arrQueue = new int(maxItems);
if(q.arrQueue == Null)
return 0; // không c p phát đ c b nhấ ượ ộ ớ
q.max = maxItems;
q.numItems = 0; // ch a có ph n t nào trong queueư ầ ử
q.front = q.rear = -1;
return 1; // kh i t o thành côngở ạ
}
Hàng đ i, s d ng m ngợ ử ụ ả
Thao tác ki m tra hàng đ i r ngể ợ ỗ
int IsEmpty(const Queue q)
{
if(q.numItems == 0)
return 1; // Queue r ngỗ
return 0; // Queue không r ngỗ
}