Hướng dẫn giải đề thi thử đại học môn Toán số 15: Kinh nghiệm và phương pháp

HƯỚNG DẪN GIẢI ĐỀ THI THỬ ĐẠI HỌC SỐ 15 CỦA BOXMATH.VN

Môn: Toán

Câu I (2 điểm) Cho hàm số 4 3 2

( 1) (3 1) 3( 1) 1

y x m x m x m x

       

( )

2. Tìm tất cả các giá trị thực của tham số

để

( )

có ba cực trị với hoành độ ba điểm cực trị

là

1 2 3

, ,

x x x

thỏa mãn 3 3 3

1 2 3

1 1 1 127

x x x

  

Lời giải

Ta có





















3 2 2

' 4 3 1 2 3 1 3 1 1 4 3 1 3 3

y x m x m x m x x m x m

 

            

 

Ham số có 3 cực trị khi và chỉ khi

   

 

9 8 2

3 1 48 1 0 3

9 8 2

4 3 1 3 3 0

9 8 2

8 0

m m

m m m















   

  

 



  



     



 













Khi đó

( )

có 3 cực trị là 3



và

1 2

x x

là 2 nghiệm của phương trình





4 3 1 3 3 0

x m x m

    

Theo định lý Viét ta có: 1 2 1 2

3 1 3 3

;

4 4

m m

x x x x

 

   .

Ta có 3 3 3 3 3

1 2 3 1 2

1 1 1 127 1 1 100

27 27

x x x x x

     









 

1 2 1 2 1 2

3 3

1 2

3 2

100

3 1 3 3 3 1

3. .

100

4 4 4

3 3

73 435 363 65 0

5 73 70 13 0

35 2 69

x x x x x x

x x

m m m

  

 

  

  

 

 

 



 

 

 

    



 

 



 



 







So với điều kiện ta nhận được

 

Vậy

 

thỏa mãn yêu cầu bài toán.

Câu II (2 điểm)

1. Giải phương trình:

 

3 2

cos 4cos 1

sin cos cos 2

x x

x x x

  

.

Lời giải

Điều kiện: sin cos 0 sin 2 0 ,

x x x x k Z



     

Khi đó phương trình tương đương với

 

3 2 2

2 2

2 2 2

cos 4cos 1 3sin cos 2 3sin cos 0

cos cos 3sin 2cos 2 cos2 3 sin 2 0

cos cos cos 1 cos 2 0

3 3

cos cos cos 0

2 6 6

cos cos

2 6 2 6

x x x x x x

x x x x

x x

 

    

      

   

      

   

   

   

    

   

   

 

   

   

   

   

 

4cos 0

3 3 5

cos cos 0 cos cos

2 6 2 6 2 6 2 6

cos 0 cos 0

6 6

3 5 2

2 6 2 6 3

3 5 2

2 6 2 6

6 2

x x x x

x x

x x kx k

x x k

x k



   

 

  



  

 

  

 

 

 

       

      

       

 

         

 

 

   

 

   

   

 

   

 

     



 

    













22 ,

x k k Z

x k













   

  







 





Vậy phương trình có nghiệm 22 ,

x k k Z



  

Câu II (2 điểm)

2. Giải phương trình: 3 3 2

162 2 27 9 1 1

x x x

    

Lời giải

Đặt 33 3 3

162 2 162 2

y x y x

    

Ta cũng có: 2 2 2 2

2 27 9 6 12 162 54

y y x x y y x x

      

Cộng lại ta được: 3 2 3 2

6 12 8 162 162 54 6

y y y x x x

      

 





     

3 3 3

3 2 3

2 6 27 27 9 1 2 6 3 1 2 6 3 1

y x x x y x y x

             

Thay ngược lại ta có:

       

3 3 3 3

6 3 1 6 3 1 2 9 3 1 6 6 3 1 2 9

x x x x x x

   

        

   





 

3 33

3 3 3

3 3

4 9 12

36 2 6 36

3 36 36 2 6 9

3 36 9 3 3 12 9

x x x



       

.

Vậy phương trình có nghiệm duy nhất

x 

Câu III (1 điểm) Tính tích phân:

3 2

2 2

sin cos 2sin

cos 1 sin

x x x x

I dx

x x







.

Lời giải

Đặt 2

sin cos

1 sin

u x

du dx

x xdx

v x







 



 

 









Do đó

2 2

2 20

2sin 6

1 sin 1 sin 8

cos 1 sin

I x x x dx H

x x



 

      

 



 



Với

2 20

2sin

1 sin cos 1 sin

H x dx

x x



 

  

 



 



 

2 2 2 2

4 4 2

2 2 20 0

2 2

1 sin cos sin 1 sin tan .sin .cos

( )

cos 1 sin 1 sin

1 sin (tan ) tan . 1 sin

tan 1 sin

x x x x x x x

dx dx

x x x

xd x x d x

x x

 



  

  

 

   

  

 



Vậy

6 6

8 2



  .

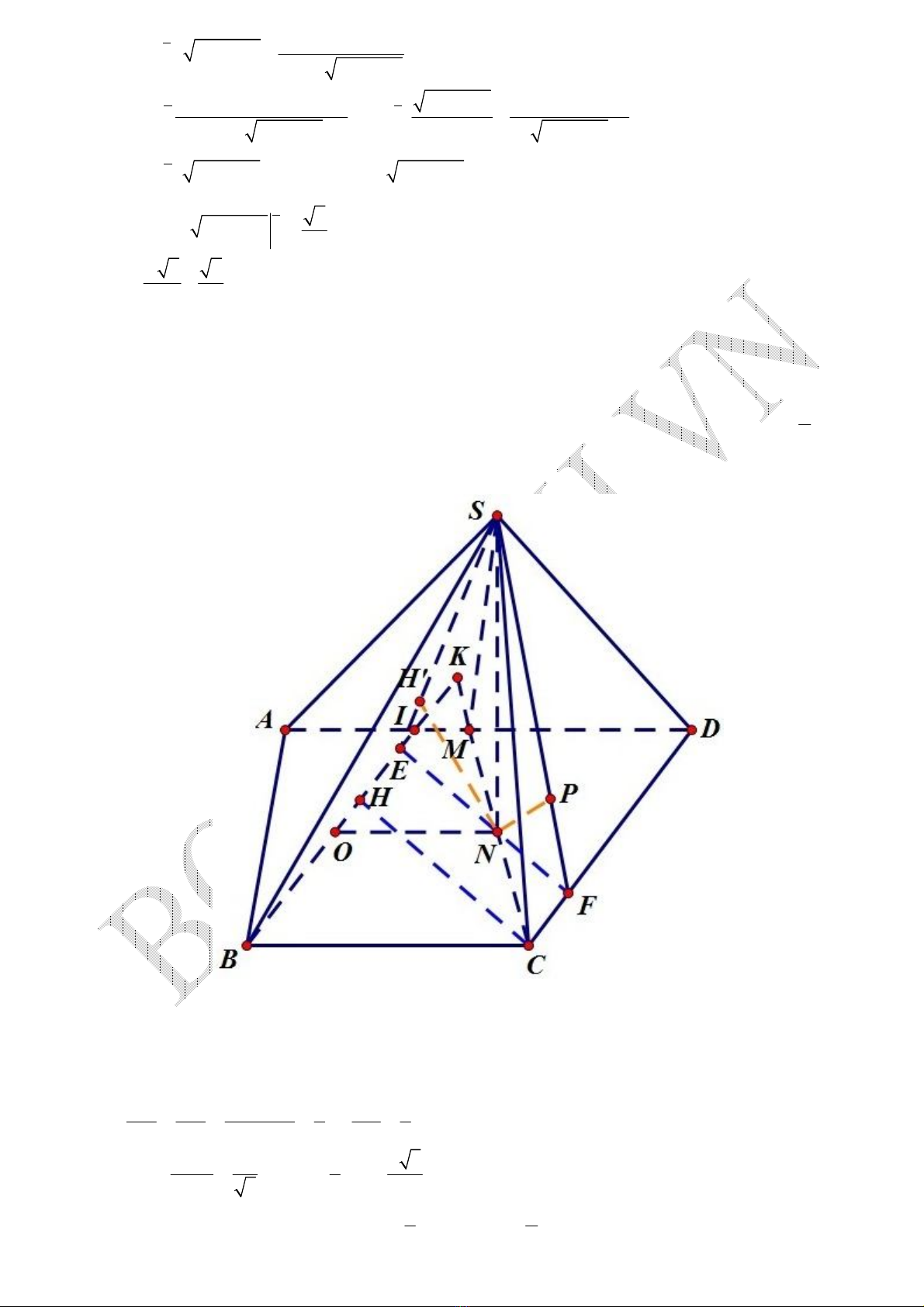
Câu IV (1 điểm) Cho hình chóp .

S ABCD

có đáy

ABCD

là hình thang vuông tại

( / / )

AD BC

AB BC a

 

AD a



. Gọi

là trung điểm của

. Biết

( )

SNA

( )

SNB

cùng vuông góc với mặt phẳng đáy và khoảng cách giữa hai đường thẳng

SB CD

bằng

Tính

thể tích khối chóp đã cho và khoảng cách từ

đến mặt phẳng

( )

SCD

theo

Lời giải

- Tính thể tích

Từ giả thiết dễ thấy

vuông

( )

ABCD

Kẻ

/ / ( )

BI CD I AD



, kẻ

vuông

tại

/ / ( , , ), / / ( )

EF CH N EF E BI F CD NO BC O BI

   

Kéo dài

cắt

tại

Trong

( )

SNE

kẻ

vuông góc với

tại

thì ( ,( ))

d N SBI NH





Ta có

5 5

2 8 8

KN ON IM BC

KC BC BC



    

4 5 5

8 2

IBC

S a a

EF CH EN EF

     

( , ) ( ,( )) ( ,( )) ( ,( ))

5 2

d SB CD d CD SBI d F SBI d N SBI

   

Suy ra

( ,( ))

d N SBI H N



  . Áp dụng

2 2 2

1 1 1

SN EN H N

 



236

SN 

1 25

. .

3 236

S ABCD ABCD

V SN S   .

- Tính khoảng cách

Trong

( )

SNF

kẻ

vuông

tại

,thì ( ,( ))

d N SCD NP



Vì

là trung điểm

nên ( ,( ) 2 ( ,( )) 2

d M SCD d N SCD NP

 

Áp dụng

2 2 2

1 1 1

SN NF NP

 

8 41

NP 

Vậy

( ,( )

4 41

d M SCD .

Câu V (1 điểm) Cho

, ,

abc

là các số thực dương thỏa mãn

abc

  

Chứng minh rằng:

2 2 2

2 2 2 1 1 1 2

9 .

a b c a b c abc

      

Lời giải

Cách 1:

Đặt

1 1 1

, ,x y z

a b c

  

Khi đó ta có 1 1 1

x y z



tương đương

xy yz zx xyz



và ta cần chứng minh

2 2 2

2( ) 9 2 2( ).

x y z x y z xyz x y z xy yz zx

           



Bây giờ giả sử thằng

là bé nhất trong ba số

, , .

x y z

Và chú ý rằng

2 2 2 2

2( ) 2( ) 2( )( ),

x y z xy yz zx x y x z y z

         

và









    

  

     

xy yz zx x y z

x y z xyz

xy yz zx x y z xy yz zx

xyz

xy yz zx x y z xyz

xyz

z x y x y x z y z

xyz

    

   

      



    



    



Như vậy, bất đẳng thức cần chứng minh được viết dưới dạng 2

.( ) .( )( ) 0.

M x y N x z y z   



Trong đó 2

2 , 2 .

x y

M N

xy xyz



   

Vì

bé nhất nên ta chỉ cần chứng minh

, 0.

M N



Thật vậy, ta có

  

1 1 1 2 1 3

•1 9

2 2 16 0.

1 1 1 1

•1 1

x y z xy xy xy

Mxy xy

x y z z

xyz xy z x y

xyz x y xyz xy yz zx x y

Nxyz xyz xyz

     



  

     

   

      

    

 



Bài toán được chứng minh xong

Đẳng thức xảy ra khi và chỉ khi

x y z

  

hay

a b c

  

Cách 2:

Từ điều kiện ta có:

0 , , 1

abc

 

Ta sẽ chứng minh

2 2

1 1 2 ( )

a b

a b ab ab



  

Thật vậy bất đẳng thức trên tương đương với 2

( ) (1 ) 0

a b ab

  

(đúng theo điều kiện)

Tương tự ta cũng có:

2 2

1 1 2 ( )

b c

b c bc bc

c a

c a ca ca



  





Cộng 3 bất đẳng thức trên ta được:

2 2 2

2 2 2 2 2 2 ( ) ( ) ( )

2 2 2 2( ) ( )( ) 9

2 2 2 1 1 1 2

c a b a b c b c a

a b c ab bc ca abc

a b c a b c ab bc ca abc

a b c abc abc

a b c a b c abc

    

     

      

    

       

Vậy bất đẳng thức đã được chứng minh.

Dấu bằng xảy ra khi và chỉ khi

abc

  

Câu VI.a (2 điểm)

1. Trong mặt phẳng

Oxy

, cho đường tròn

   

2 2

( ) : 1 5 25

C x y

   

có tâm

. Tìm điểm

thuộc đường thẳng



sao cho từ

kẻ được 2 tiếp tuyến ,

MA MB

(

A B

là tiếp điểm) đến đường

tròn

( )

và khoảng cách từ

đến

bằng

842

. Biết điểm

có hoành độ dương.

Lời giải

Đường tròn

( )

có tâm

(1;5)

I, bán kính



Gọi tọa độ điểm

là

( ;4)

M m .

Gọi

có tọa độ:

1 1

( ; )

A x y

, ta có 2 2

1 1

( 1) ( 5) 25

A C x y

     

Phương trình đường thẳng

là 1 1

( 1)( 1

) ( 5)( 5) 25

x x y y     

M MA



nên ta có: 1 1 1 1

( 1)( 1) ( 5) 25 ( 1) 19 0 (1)

m x y m x y m          

Hoàn toàn tương tự, gọi

2 2

( ; )

B x y

thì ta có: 2 2

( 1) 19 0 (2)

m x y m    

Từ (1) và (2) ta có phương trình đường thẳng

là

( 1) 19 0

m x y m

    

Khoảng cách từ

đến

bằng

842

| ( 1).1 5 19 | 25

( 1) 841 30

842

( 1) 1

m m m m





   

       

 

   (do



)

Vậy điểm

cần tìm có tọa độ

(30;4)

2. Trong không gian

Oxyz

, cho đường thẳng :

d x y z

 

và hai điểm

(0;0;3), (0;3;3)

A B . Tìm

tọa độ điểm

nằm trên đường thẳng

sao cho tam giác

ABC

có chu vi nhỏ nhất.

Lời giải

Phương trình tham số đường thẳng :

x t

d y t

z t

















Hướng dẫn giải đề thi thử đại học số 15 môn: Toán

Chủ đề:

Tài liệu liên quan

Tài liêu mới

AI tóm tắt

Giới thiệu tài liệu

Đối tượng sử dụng

Từ khoá chính

Nội dung tóm tắt

Hỗ trợ

Phương thức thanh toán

Theo dõi chúng tôi