UBND T NH TH A THIÊN HUỈ Ừ Ế KÌ THI TUY N SINH THPT CHUYÊN QU C H CỂ Ố Ọ
S GIÁO D C VÀ ĐÀO T OỞ Ụ Ạ Khoá ngày 24.6.2010 - Môn thi: TOÁN (CHUYÊN TIN)
Đ CHÍNH TH CỀ Ứ Th i gian làm bàiờ: 150 phút
Bài 1: (1,5 đi mể) Không s d ng máy tính c m tay, rút g n các bi u th c:ử ụ ầ ọ ể ứ
a)
2 3 6 8 4
2 3 4
A+ + + +
=+ +
.b)
( )
310 6 3. 3 1
6 2 5 5
B
+ −
=+ −
.
Bài 2: (1,5 đi mể) Cho ph ng trình ươ
2
2 9 0x mx− + =
(m là tham s )ố
a) V i giá tr nào c a ớ ị ủ m thì ph ng trình có nghi m ?ươ ệ
b) Trong tr ng h p ph ng trình có nghi m, tìm giá tr c a ườ ợ ươ ệ ị ủ m đ t ng các lũy th aể ổ ừ
b c b n c a hai nghi m c a ph ng trình b ng 799.ậ ố ủ ệ ủ ươ ằ
Bài 3: (1,5 đi mể)
M t đám đ t hình ch nh t có chi u r ng b ng ộ ấ ữ ậ ề ộ ằ
2
3
chi u dài. N u b t m i c nh 5m thìề ế ớ ỗ ạ
di n tích đám đ t gi m đi 16%. Tính chi u dài và chi u r ng ban đ u c a đám đ t..ệ ấ ả ề ề ộ ầ ủ ấ
Bµi 4: (3,5 đi mể)
a) Cho đ ng tròn (O, R) và đi m I trong đ ng tròn. Qua I v hai dây cung b t kỳườ ể ở ườ ẽ ấ
MIN và PIQ. G i M’, N’, P’, Q’ l n l t là trung đi m c a IM, IN, IP, IQ . ọ ầ ượ ể ủ
1) Ch ng minh r ng t giác M’P’N’Q’ là t giác n i ti p.ứ ằ ứ ứ ộ ế
2) Gi s I thay đ i, các dây MIN và PIQ thay đ i. Ch ng minh r ng đ ng trònả ử ổ ổ ứ ằ ườ
ngo i ti p t giác M’P’N’Q’có bán kính không đ i.ạ ế ứ ổ
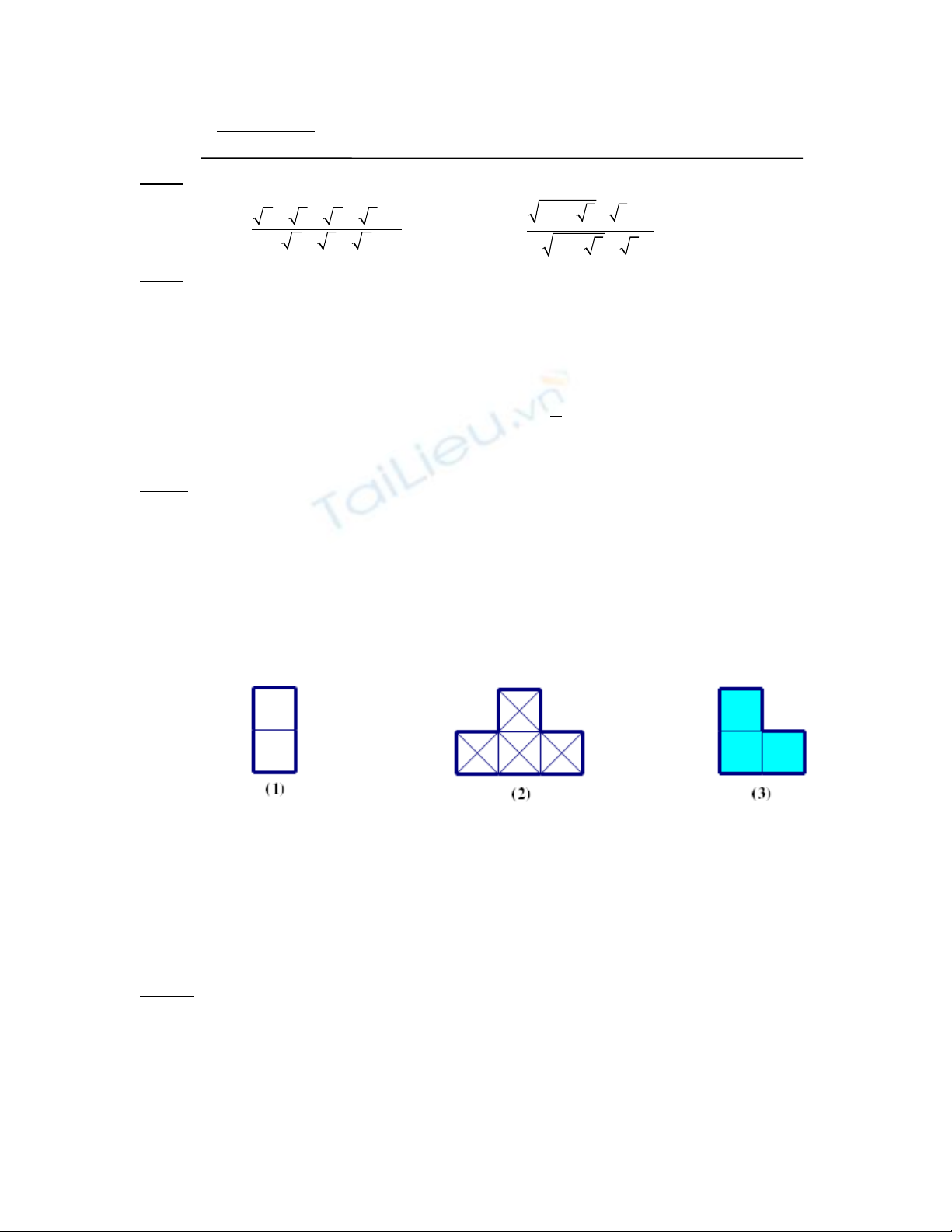
b) M t ng i dùng 03 lo i g ch nh sau (xem hình v ) đ lát sàn nhà hình vuông cóộ ườ ạ ạ ư ẽ ể
di n tích 36 ệ× 36 (dm2).
(M i ô vuông nh có kích th c 1 ỗ ỏ ướ × 1 (dm2))
Bi t lo i g ch (1) có giá 950 đ ng/viên; lo i g ch (2) có giá 1350 đ ng/viên; lo i g chế ạ ạ ồ ạ ạ ồ ạ ạ
(3) có giá 1050 đ ng/viên. ồNg i đó ghép các lo i g ch trên thành hai m u sau, r i ch dùngườ ạ ạ ẫ ồ ỉ
m t trong hai m u y đ lát sàn nhà: ộ ẫ ấ ể M u 1ẫ: có kích th c ướ
3 3×
(dm2); M u 2ẫ: có kích
th c ướ
3 4×
(dm2).
Bi t r ng trong m i m u ghép ph i có đ y đ ba lo i g ch trên. Hãy v hình mô t haiế ằ ỗ ẫ ả ầ ủ ạ ạ ẽ ả
m u ghép trên và cho bi t lát sàn theo m u ghép nào t n ti n ít h nẫ ế ẫ ố ề ơ ?
B µi 5: (2,0 đi mể)
a) Tìm t t c các dãy s t nhiên ch n liên ti p có t ng b ng 2010ấ ả ố ự ẵ ế ổ ằ .
b) Môt thung đ ng $ % ư$ n lit r u (& ươ$ n là s nguyên d ng). Ng i ta muôn đong hêt đê lamố ươ ươ% & & ' %
rông thung r u ma chi dung hai binh: môt binh co dung tich la 1 lit va binh kia co dung tich( % ươ$ % ' % % $ % & & % & % % & &
la 2 lit; môi thao tac đong chi dung môt loai binh. Goi % & ( & ' % $ $ % $ S(n) la sô cach đong theo th t cac% & & ư& ư$ &
thao tac đong đê lam rông thung đ ng & ' % ( % ư$ n lit r u. Hay liêt kê cac cach đong đo đê tinh S(1),& ươ$ ( $ & & & ' &
S(2), S(3), S(4), S(5), S(6). T đo rut ra quy lu t đê tinh ư% & & ậ ' & S(n) (không c n ch ng minh). Apầ ứ &
dung đê tinh S(10).$ ' &
HÕt
SBD thí sinh: ............... Ch ký GT1: ................................ữ
2
UBND T NH TH A THIÊN HUỈ Ừ Ế KÌ THI TUY N SINH LỂPỚ 10 CHUYÊN TIN QUÔC H CỌ
S GIÁO D C VÀ ĐÀO T OỞ Ụ Ạ Môn thi: TOÁN - Năm h c 2010-2011ọ
Đ CHÍNH TH CỀ Ứ §¸p ¸n vµ thang ®iÓm
Bµi ý Néi dung §iÓm
11,5
1.a
(0,75)
( )
2 3 2 2 3 2 2
2 3 6 8 4
2 3 4 2 3 2
A+ + + + +
+ + + +
= =
+ + + +
1 2= +
0,5
0,25
1.b
(0,75) Ta có:
Suy ra:
( )
2
6 2 5 5 5 1 5 5 1 5 1+ − = + − = + − =
V y:ậ
( )
+ −
= =
+ −
310 6 3. 3 1 2
6 2 5 5
B
0,25
0,25
0,25
21,50
2.
a
(0,5
)
Ph ng trình ươ
2
2 9 0x mx− + =
(2) có:
2
' 9m∆ = −
Đ ph ng trình có nghi m c n và đ là:ể ươ ệ ầ ủ
2
' 9 0 3 3 3m m m hay m∆ = − ≥ ⇔ ≥ ⇔ ≤ − ≥
(*)
0,25
0,25
2.b
(1,0
)
+ V i đi u ki n (*), ph ng trình (2) có hai nghi m ớ ề ệ ươ ệ
1
x
và
2
x
.
Theo đ nh lý Vi-ét: ị
1 2
2x x m+ =
vµ
1 2
9x x =
Theo gi thi t: ả ế
( )
( )
22
4 4 2 2
1 2 1 2 1 2
799 2 799x x x x x x+ = ⇔ + − =
( ) ( )
( )
22
2 2 2
1 2 1 2 1 2
2 2 799 4 18 162 799x x x x x x m
⇔ + − − = ⇔ − − =
4 2
16 144 637 0m m⇔ − − =
(**)
Đ t: ặ
2
0t m= ≥
, ph ng trình (**) tr thành:ươ ở
2
16 144 637 0t t⇔ − − =
.
Gi i ph ng trình ta đ c: ả ươ ượ
1 2
12,25 ; 3,25 0t t= = − <
(lo i)ạ
V i ớ
2
12,25 3,5t m m= = ⇔ = ±
(
3m≥
th a đi u ki n (*)ỏ ề ệ
V y:ậ §Ó
4 4
1 2
799x x+ =
thì
3,5m= ±
0,25
0,25
0,25
0,25
31,5
G i chi u dài đám đ t là ọ ề ấ x (m). Đi u ki n: ề ệ
25 7,5 ( )
3x x cm> ⇔ >
.
Khi đó chi u r ng đám đ t là ề ộ ấ
2
3x
(m) và di n tích đám đ t là ệ ấ
2
2
3x
(m2)
0,25
0,25
Di n tích ệđám đ t sau khi b t m i c nh 5m: ấ ớ ỗ ạ
( )
2
5 5
3
x x
− −
÷
(m2) 0,25
Ta có ph ng trình ươ
( )
2 2
2 2 2
5 5 16%
3 3 3
x x x x
− − − = ×
÷
2
32 2500 7500 0x x⇔ − + =
.
Gi i ph ng trình ta có ả ươ
1 2
75; 3,125 7,5x x= = <
(lo i)ạ
0,25
0,25
1
V y chi u dài đám đ t là 75 ậ ề ấ (m) và chi u r ng là ề ộ
2.75 50( )
3m=
0,25
43,5
4.a.
1
(1,0)
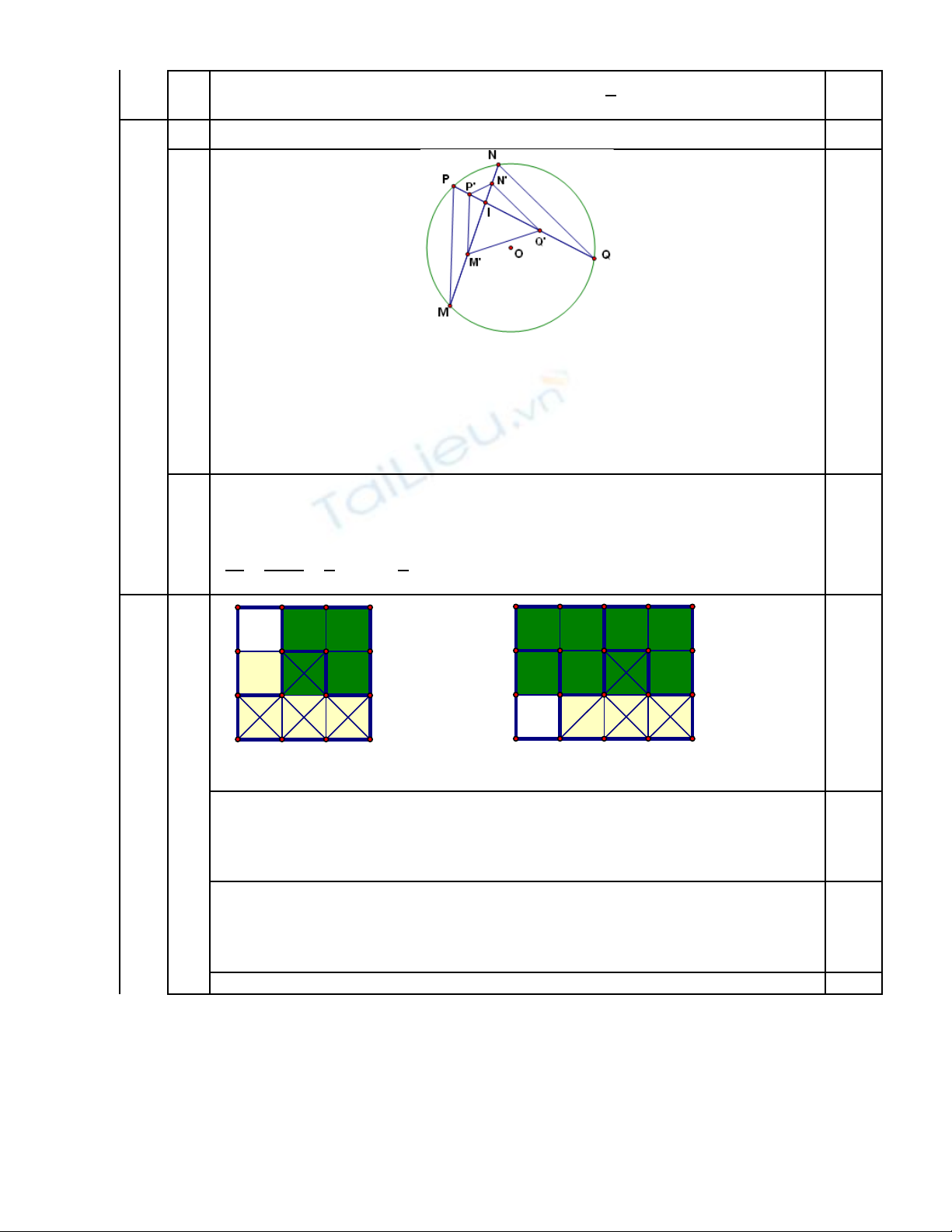
Hình v đúngẽ
Ta có góc
·
·
·
·
' ' ' ; ' ' 'P M N PMN N Q P NQP= =
(góc so le trong)
Mà
·
·
PMN NQP=
(Góc n i ti p cùng ch n cung ộ ế ắ
»
NP
).
Nên
·
·
' ' ' ' ' 'P M N N Q P=
V y t giác M’P’N’Q’ là t giác n i ti p.ậ ứ ứ ộ ế
0,25
0,50
0,25
4.a.
2
(0,75)
Đ ng tròn ngo i ti p t giác ườ ạ ế ứ M’P’N’Q’ là đ ng tròn ngo i ti p tam giácườ ạ ế
M’N’Q’ gi s nó có bán kính R’.ả ử
Do
'M N Q
′ ′
∆
đ ng d ng v i ồ ạ ớ
MNQ∆
(g-g) suy ra:
1 1
2 2
R M N R R
R MN
′ ′ ′ ′
= = ⇒ =
(Không đ i, đpcm)ổ
0,25
0,25
0,25
4.b
(1,75)
Cách ghép 1 Cách ghép 2
0,50
V i m u ghép 1ớ ẫ : Kinh phí cho m i m u 3 ỗ ẫ × 3 (dm2) là:
950 1350 1050 3350+ + =
(đ)
Đ lát h t sàn nhà kích th c 36 ể ế ướ × 36 (dm2) c n ầ
12 12 144× =
m u g ch 3 ẫ ạ ×
3 (dm2) nên s ti n c n dùng là: ố ề ầ
144 3350 482400× =
(đ)
0,25
0,25
V i m u ghép 2ớ ẫ : Kinh phí cho m i m u 3 ỗ ẫ × 4 (dm2) là:
950 1350 2 1050 4400+ + × =
(đ)
Đ lát h t sàn nhà kích th c 36 ể ế ướ × 36 (dm2) c n ầ
12 9 108
× =
m u g ch 3 ẫ ạ ×
4 (dm2) nên s ti n c n dùng là: ố ề ầ
108 4400 475200× =
(đ)
0,25
0,25
Nh v y, lát sàn theo cách th 2 t n ít ti n h n.ư ậ ứ ố ề ơ 0,25
2
52,0
5.
a
(1,0
)
G i 2ọx là s t nhiên ch n đ u tiên c a dãy. Theo gi thi t ta có:ố ự ẵ ầ ủ ả ế
( ) ( ) ( )
2 2 2 2 4 ... 2 2 2010 ( 1)x x x x y y+ + + + + + + = ≥
( ) ( ) ( )
1 2 ... 1005x x x x y⇔ + + + + + + + =
( )
1 1 2 ... 1005y x y⇔ + + + + + =
( ) ( ) ( ) ( )
1
1 1005 1 2 2010
2
y y
y x y x y
+
⇔ + + = ⇔ + + =
Suy ra
( )
1y+
là c s c a ướ ố ủ
2010 1 2 3 5 67
= × × × ×
.
Nên:
( ) { }
1 2,3,5,6,10,15,30,67,134,201,335,402,670,1005,2010y+ ∈
(vì
1y≥
)
{ }
1,2,4,5,9,14,29,66,133,200,334,401,669,1004,2009y⇔ ∈
+ V i ớ
1y=
:
2 1 1005 2 1004x x
+ = ⇔ =
, dãy s c n tìm là: 1004;ố ầ 1006.
+ V i ơ&
2y=
:
2 2 670 2 668x x
+ = ⇔ =
, dãy s c n tìm là: 668, 670, 672.ố ầ
+ V i ớ
4y=
:
( )
5 2 4 2010 2 398x x+ = ⇔ =
, dãy s c n tìm là: 398; 400; 402;ố ầ
404; 406.
+ V i ớ
5y=
:
( )
6 2 5 2010 2 330x x+ = ⇔ =
, dãy s c n tìm là: ố ầ
330; 332; 334; 336; 338; 340.
+ V i ớ
9y=
:
( )
10 2 9 2010 2 192x x+ = ⇔ =
, dãy s c n tìm là: ố ầ
192;194;196; 198; 200; 202; 204; 206; 208; 210.
+ V i ớ
14y=
:
( )
15 2 14 2010 2 120x x+ = ⇔ =
, dãy s c n tìm là: ố ầ
120; 122; 124; 126; ...; 148.
+ V i ớ
29y=
:
( )
30 2 29 2010 2 38x x+ = ⇔ =
, dãy s c n tìm là: ố ầ
38; 40; 42; 44; 46; ...; 96.
+ V i ớ
67y≥
:
( )
2 30 2 0x y x+ ≤ ⇔ <
.
V y: Ch có 7 dãy s t nhiên ch n liên ti p tho đi u ki n bài toán là:ậ ỉ ố ự ẵ ế ả ề ệ
1) 1004; 1006
2) 668; 670; 672
3) 398; 400; 402; 404; 406
4) 330; 332; 334; 336; 338; 340
5) 192;194; 196; 198; 200; 202; 204; 206; 208; 210.
6) 120; 122; 124; 126; ...; 148
7) 38; 40; 42; 44; 46; ...; 96
0.25
0.25
0,50
3