1
BỘ GIÁO DỤC VÀ ĐÀO TẠO
ĐẠI HỌC ĐÀ NẴNG
PHẠM TRƯỜNG TÙNG
THIẾT KẾ ĐIỀU KHIỂN ĐỒNG BỘ
ROBOT 4 BẬC TỰ DO
CHUYÊN NGÀNH: SẢN XUẤT TỰ ĐỘNG
MÃ SỐ: 60.52.60
TÓM TẮT LUẬN VĂN THẠC SĨ KỸ THUẬT
ĐÀ NẴNG – NĂM 2011
2
Công trình ñược hoàn thành tại
ĐẠI HỌC ĐÀ NẴNG
Người hướng dẫn khoa học: PGS.TS. Phạm Đăng Phước
Phản biện 1:
Phản biện 2:
Luận văn ñược bảo vệ trước Hội ñồng chấm Luận văn tốt nghiệp thạc
sĩ kĩ thuật họp tại Đà Nẵng vào ngày…..tháng…..năm 2011
Có thể tìm hiểu luận văn tại:
- Trung tâm Thông tin Học liệu – ĐH Đà Nẵng.
- Trung tâm Học liệu – ĐH Đà Nẵng.
3
MỞ ĐẦU
1. Lý do chọn ñề tài:
• Hiện nay, với nền sản xuất công nghiệp hiện ñại, robot công
nghiệp là một trong những thành phần quan trọng.
• Nhiều cơ sở ñào tạo hiện chưa có robot ñể phục vụ cho sinh
viên học tập và nghiên cứu.
• Cần thiết phải nghiên cứu về robot công nghiệp nhằm nắm
bắt và phát triển kĩ thuật robot ñể phục vụ cho nhu cầu sản
xuất, phục vụ học tập, nghiên cứu.
2. Mục ñích của ñề tài:
• Đề tài tập trung nghiên cứu kĩ thuật ñiều khiển các trục khớp
ñồng thời ( ñiều khiển ñồng bộ các khớp) và áp dụng vào cho
robot 4 bậc tự do.
3. Phạm vi và nội dung nghiên cứu:
3.1. Phạm vi:
• Nghiên cứu ñể áp dụng cho robot 4 bậc tự do, sử dụng ñộng
cơ ñiện một chiều.
3.2. Nội dung nghiên cứu:
• Nghiên cứu lý thuyết về robot công nghiệp. Trên cơ sở ñó, ta
vận dụng lựa chọn mô hình robot phù hợp.
• Xây dựng mô hình toán học ñể ñiều khiển ñồng bộ các trục
của robot ñã lựa chọn. Mô hình hóa luật ñiều khiển ñó bằng
máy tính và sau ñó thiết kế bộ ñiều khiển ñồng bộ chuyển
ñộng các trục của robot.
• Chế tạo mô hình robot..
4. Phương pháp nghiên cứu:
• Nghiên cứu các tài liệu liên quan nhằm tổng hợp lựa chọn
các phương án từ ñó ñưa ra mô hình robot phù hợp, trên cơ
4
sở ñó tính toán ñể thiết kế bộ ñiều khiển ñồng bộ các trục cho
robot.
• Chế tạo mô hình ñể kiểm chứng các kết quả.
5. Ý nghĩa khoa học và thực tiễn:
• Áp dụng cho các sản phẩm là robot hoặc thiết bị tự ñộng nhiều
trục yêu cầu chuyển ñộng ñồng bộ trong quá trình hoạt ñộng.
• Góp phần thúc ñẩy việc xây dựng các mô hình phục vụ cho
công tác ñào tạo sinh viên.
• Tạo ra phương pháp học tập nghiên cứu trực quan bằng mô
hình cụ thể. Bước ñầu tiếp cận kĩ thuật ñiều khiển robot.
6. Cấu trúc của luận văn:
Cấu trúc của luận văn gồm có bốn chương.
- Chương 1: Trình bày tổng các vấn ñề quan về robot; về lịch sử
phát triền robot công nghiệp; các khái niệm cơ bản của robot
công nghiệp.
- Chương 2: Trình bày cơ sở ñể chọn lựa cấu hình robot dựa trên
các ñặc tính kĩ thuật yêu cầu. Sau khi xác ñịnh ñược mô hình
robot, ta tiến hành tính toán ñộng học và ñộng lực học của mô
hình robot ñó.
Chương 3: Trình bày về các khái niệm về ñiều khiển ñồng bộ;
thiết kế quy luật chuyển ñộng của các trục khớp. Trên cơ sở quy
luật chuyển ñộng ñó, ñề ra mô hình ñiều khiển ñồng bộ các trục
khớp thông qua việc xây dựng phương pháp ñiều khiển theo
phương pháp trượt. Sau khi xây dựng mô hình toán học, tiến
hành mô phỏng trên Matlab ñể kiểm nghiệm.
- Chương 4. Chương này trình bày cơ sở thiết kế mạch ñiều khiển
và chương trình ñiều khiển robot trên máy tính ñược lập trình
bằng ngôn ngữ Visual Basic.
5
CHƯƠNG 1 - TỔNG QUAN
1.1. LỊCH SỬ PHÁT TRIỂN CỦA ROBOT CÔNG NGHIỆP
1.2. CÁC KHÁI NIỆM VÀ ĐỊNH NGHĨA VỀ ROBOT CÔNG
NGHIỆP
1.3. KẾT CẤU CƠ BẢN CỦA MỘT ROBOT CÔNG NGHIỆP
1.3.1. Kết cấu chung
1.4. PHÂN LOẠI ROBOT CÔNG NGHIỆP
1.4.1. Phân loại theo kết cấu
1.4.2. Phân loại theo hệ thống truyền ñộng
1.4.3. Phân loại theo ứng dụng
1.4.4. Phân loại theo cách thức và ñặc trưng của phương pháp
ñiều khiển
CHƯƠNG 2 - LỰA CHỌN MÔ HÌNH ROBOT – TÍNH TOÁN
ĐỘNG HỌC VÀ ĐỘNG LỰC HỌC
2.1. LỰA CHỌN MÔ HÌNH ĐỘNG HỌC CỦA ROBOT
2.1.1. Yêu cầu kĩ thuật của robot
2.1.1.1.Sức nâng của tay máy
Sức nâng của robot từ 0.1kg ñến khoảng 2kg.
2.1.1.2.Số bậc tự do của phần công tác
Ta chỉ quan tâm nghiên cứu ñối với mô hình ñộng học robot có 4
bậc tự do.
2.1.1.3.Trường công tác của robot
Hình chiếu bằng của trường công tác phải là một hình tròn ñể
ñảm bảo việc robot có thể nhặt ñược tất cả các vật ở vị trí xung quanh
gốc cố ñịnh của nó.
6
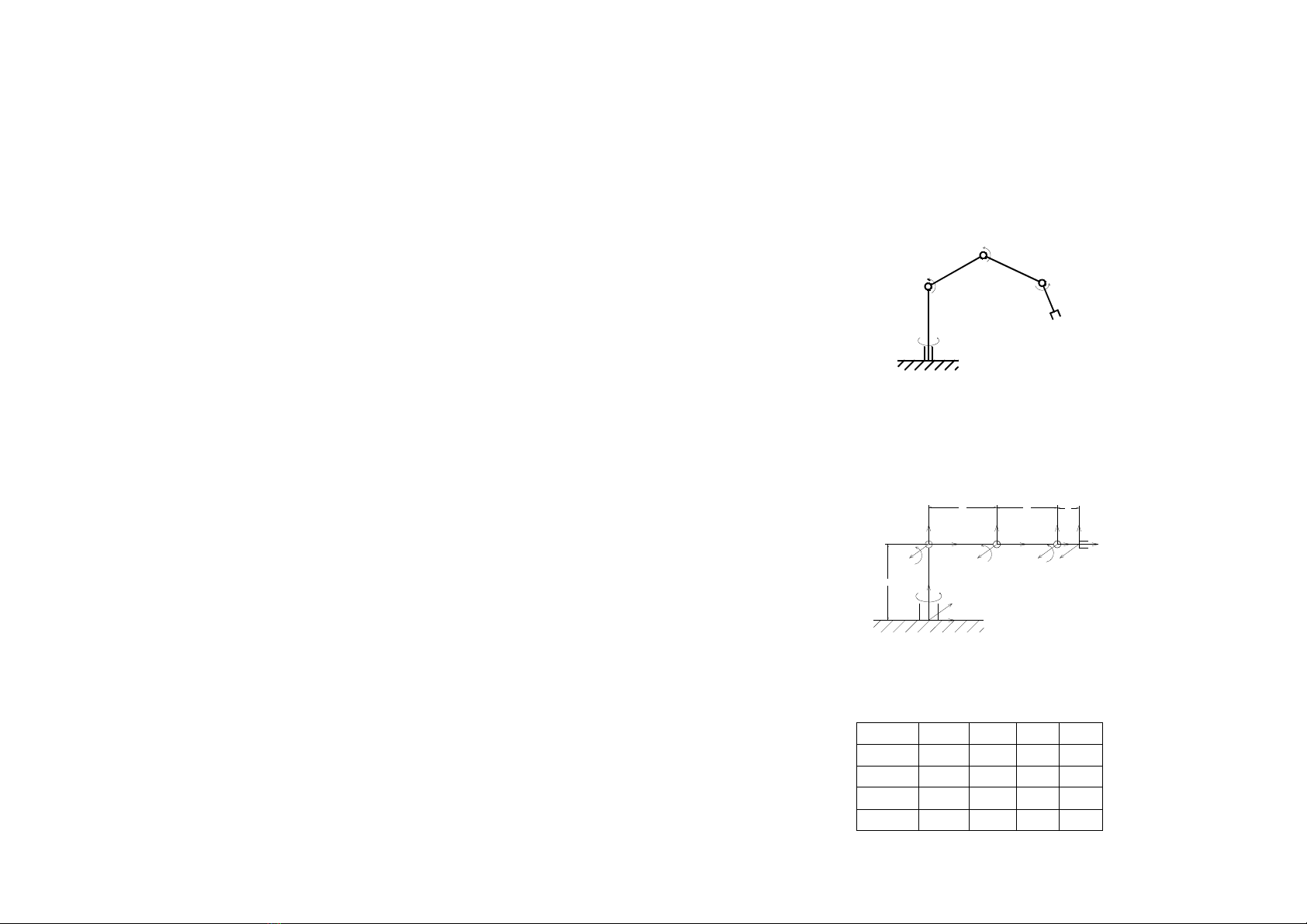
2.1.2. Lựa chọn mô hình ñộng học của robot
Trong các loại kết cấu của robot mà ta nghiên cứu ở trên, robot
của ta chỉ có thể có một trong các kết cấu kiểu tọa ñộ trụ, tọa ñộ cầu,
SCARA, và kiểu tay người.
Sau khi phân tích các mô hình ñã nêu trên, ta chọn mô hình kết
cấu robot kiểu tay người ñể thực hiện.
θ
1
θ
2
θ
3
θ
4
Hình 2.1. Mô hình ñộng học của robot PDU01
2.2. TÍNH TOÁN ĐỘNG HỌC CHO MÔ HÌNH ROBOT PDU01
2.2.1. Thiết lập phương trình ñộng học thuận về vị trí cho robot
PDU01
2.2.1.1.Chọn hệ tọa ñộ cơ sở, gắn các hệ toạ ñộ trung gian lên các khâu
a4
a3
a2
d1
Z
4
X
4
Y
4
O
4
Z
3
X
3
Y
3
O
3
Z
2
X
2
Y
2
O
2
O
1
Y
1
X
1
Z
1
O
0
Z
0
Y
0
X
0
θ
4
θ
3
θ
1
θ
2
Hình 2.3 . Hệ tọa ñộ trung gian trên các khâu
2.2.1.2.Lập bảng thông số DH
Bảng 2.1. Bảng thông số DH của robot PDU01
Khâu θ
i
α
i
a
i
d
i
1 θ
1*
90 0 d
1
2 θ
2*
0 a
2
0
3 θ
3*
0 a
3
0
4 θ
4*
0 a
4
0
7
2.2.1.3.Dựa vào các thông số của bảng DH, ta thiết lập các ma trận
A
i
Như vậy ta có các ma trận A
i
1 1
1 1
1
1
0 0
0 - 0
0 1 0 d
0 0 0 1
C S
S C
A
=
;
2 2 2 2
2 2 2 2
2
- 0 a
0 a
C S C
S C S
A
=
3 3 3 3
3 3 3 3
3
- 0 a
0 a
0 0 1 0
0 0 0 1
C S C
S C S
A
=
;
4 4 4 4
4 4 4 4
4
- 0 a
0 a
0 0 1 0
0 0 0 1
C S C
S C S
A
=
2.2.1.4.Tính các ma trận biến ñổi thuần nhất T
4 4 4 4
3
4 4 4 4
4
- 0 a
0 a
0 0 1 0
0 0 0 1
C S C
S C S
T
=
;
34 34 4 34 3 3
34 34 4 34 3 3
2
4
- 0 a
0 a
0 0 1 0
0 0 0 1
C S C a C
S C S a S
T
+
+
=
234 234 4 234 3 23 2 2
1
234 234 4 234 3 23 2 2
4
- 0 a
0 a
0 0 1 0
0 0 0 1
C S C a C a C
S C S a S a S
T
+ +
+ +
=
1 234 1 234 1 4 1 234 3 1 23 2 1 2
1 234 1 234 1 4 1 234 3 1 23 2 1 2
4234 234 4 234 3 23 2 2 1
C S a
a
S 0 a
0 0 0 1
C C S C C a C C a C C
S C S S C S C a S C a S C
TC S a S a S d
− + +
− − + +
=
+ + +
Vậy ta có hệ phương trình ñộng học thuận về vị trí của robot
PDU01 như sau:
8
Bảng 2.2. Hệ phương trình ñộng học thuận của robot PDU01
n
x
= C
1
C
234
o
x
= - C
1
S
234
a
x
= S
1
p
x
=
4 1 234 3 1 23 2 1 2
a
C C a C C a C C
+ +
n
y
= S
1
C
234
o
y
= -S
1
S
234
a
y
= -C
1
p
y
=
4 1 234 3 1 23 2 1 2
a
S C a S C a S C
+ +
n
z
= S
234
o
z
= C
234
a
z
= 0 p
z
=
4 234 3 23 2 2 1
a
S a S a S d
+ + +
2.2.2. Phương trình ñộng học ngược về vị trí cho robot PDU01
2.2.2.1.Điều kiện ñể hệ phương trình có nghiệm
0
y y
x
x y x
y
x
z
z x y
z
o p
a
o a p
o
on
o n n
a
= − =
=− = −
=
2.2.2.2.Tìm nghiệm của hệ phương trình ñộng học
Thực hiện việc giải phương trình ñộng học ngược bằng cách nhân
lần lượt các ma trận nghịch ñảo của ma trận A
i
với ma trận T
4
ta giải
ñược kết quả sau:
1
arctan 2( , )
x y
a a
θ
= −
θ
234
= - arctan2(C
1
o
x
+S
1
o
y
,o
z
)
2 2 2 2
3 2
2
3 3 2 2
3 2
=arctan2( 1 , )
x y
P P a a
Ca a
θ
+ − −
± − +
(
)
( ) ( )
(
)
( ) ( )
3 3 2 3 23 2 2 3 3 3 23 2 2 3 3 2 3 23 2 2 3 3 3 23 2 2
22 2 2 2
3 3 2 3 3 3 3 2 3 3
( ) ( ) ( ) ( )
=arctan2( , )
a C a a S a S a S a C a C a C a a C a C a S a S a S
a C a a S a C a a S
θ
+ + − + + + + +
+ + + +
4 234 2 3
=
θ θ θ θ
− −
2.3. LỰA CHỌN PHƯƠNG ÁN TRUYỀN ĐỘNG CHO ROBOT
2.3.1.Phương án truyền ñộng cho khớp thứ nhất
9
Hình 2.4. Phương án truyền ñộng cho khớp thứ nhất
2.3.2.Phương án truyền ñộng cho khớp thứ hai
Hình 2.5. Phương án truyền ñộng cho khớp thứ hai
2.3.3.Phương án truyền ñộng cho khớp thứ ba
Hình 2.6. Phương án truyền ñộng cho khớp thứ ba
2.3.4.Phương án truyền ñộng cho khớp thứ tư
Hình 2.7. Phương án truyền ñộng cho khớp thứ tư
10
2.4. ĐỘNG LỰC HỌC CỦA ROBOT PDU01
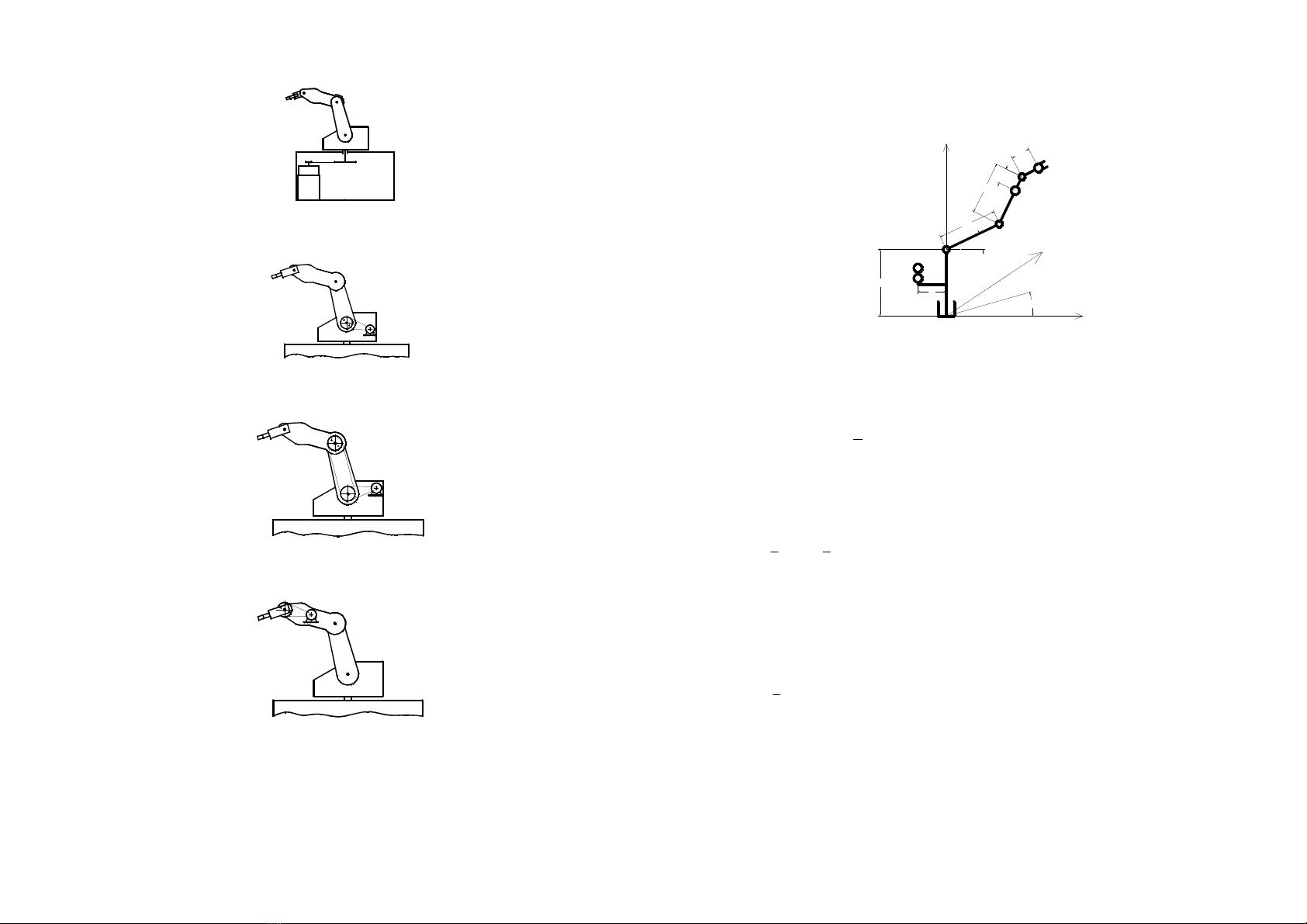
2. 4.1. Mô hình ñộng lực học của robot PDU01
d1
a4
a2
a3
l
3
l
1
Y
θ
1
m
dc2
m
dc3
m
dt
m
dc4
M
Z
X
O
A
B
C
D
θ
2
Hình 2.8. Mô hình tính toán ñộng lực học của robot PDU01
2.4.2. Tính ñộng năng và thế năng cho từng chất ñiểm
2.4.2.1. Tính ñộng năng và thế năng của chất ñiểm A và B
2
2
1
2 3 1
1( )
2
AB dc dc
K m m l
θ
•
= +
2 1 3 2
( )
AB dc dc
P m h m h g
= +
2.4.2.2. Động năng và thế năng của chất ñiểm D
2 2
2 2 2 2 2 2
4 2 2 3 3 2 3 2 3 3 3 2 2 3 2 2 1
2 2
2 2
3 3 2 3 1 2 3 3 2 2 3 1
1 1 ( ) ( ) 2 ( )cos ( ) cos
2 2
( ) cos ( ) 2 ( )cos cos( )
D D D dc
K m v m a a l a a l a
a l a a l
θ θ θ θ θ θ θ θ θ
θ θ θ θ θ θ θ
• • • • • • •
• •
= = + − + ++ − + +
+ − + + − +
[
]
4 1 2 2 3 3 2 3
sin ( )sin( )
D D D dc
P m z g m d a a l g
θ θ θ
= = + + − +
2.4.2.3.Tính ñộng năng và thế năng cho chất ñiểm M
2
2 2 2 2 2
2 2 3 2 3 4 2 3 4 2 3 3 2 2 3
2 4 3 4 2 2 3 4 3 4 4 2 3 2 3 4
2 2 2
2 2 2 2 2 2
2 2 1 3 2 3 1 4 2 3 4 1 2 3
1( ) ( ) 2 cos ( )
2
2 cos( ) ( ) 2 cos ( )( )
cos cos ( ) cos ( ) 2 cos
M
K M a a a a a
a a a a
a a a a a
θ θ θ θ θ θ θ θ θ θ
θ θ θ θ θ θ θ θ θ θ θ θ
θ θ θ θ θ θ θ θ θ
• • • • • • • • •
•••• •••••
• • •
= + + + + + + +
+ + + + + + + +
+ + + + + + +
2
2 2 3 1
2 2
2 4 2 2 3 4 1 3 4 2 3 2 3 4 1
cos( )
2 cos cos( ) 2 cos( )cos( )a a a a
θ θ θ θ
θ θ θ θ θ θ θ θ θ θ θ
•
• •
+
+ + + + + + +
[
]
1 2 2 3 2 3 4 2 3 4
sin sin( ) sin( )
M M
P Mz g M d a a a g
θ θ θ θ θ θ
= = + + + + + +