M c l cụ ụ
Ph n I : Thi t ầ ế l pậ h tr c t a đ khi phay lăn ệ ụ ọ ộ
răng..............................................................2
1.1 T ng quan v dao phay lăn răng.........................................................................2ổ ề
1.2 Thi t l p h tr c t a đ khi phay lăn ế ậ ệ ụ ọ ộ
răng..........................................................3
Ph n II : Thi t l p chuy n đi t a ầ ế ậ ể ổ ọ
đ..................................................................................4ộ
Ph n III : Tìm ph ng trình b m t kh i th y cho đi t ng ầ ươ ề ặ ở ủ ố ượ
2.........................................7
Ph n IV : Xác đnh b m t kh i th y b ng ph ng pháp đng ầ ị ề ặ ở ủ ằ ươ ộ
h c...................................9ọ
Ph n V : ng d ng Ten-x quay trong chuy n đi t a ầ Ứ ụ ơ ể ổ ọ
đ................................................11ộ
Ph n VI : Xác đnh đ cong m t, đng ti p xúc, kích th c khi phay lăn ầ ị ộ ặ ườ ế ướ
răng..............13
HN891 Page 1
Ph n I : Thi t l p h tr c t a đ khiầ ế ậ ệ ụ ọ ộ
phay lăn răng
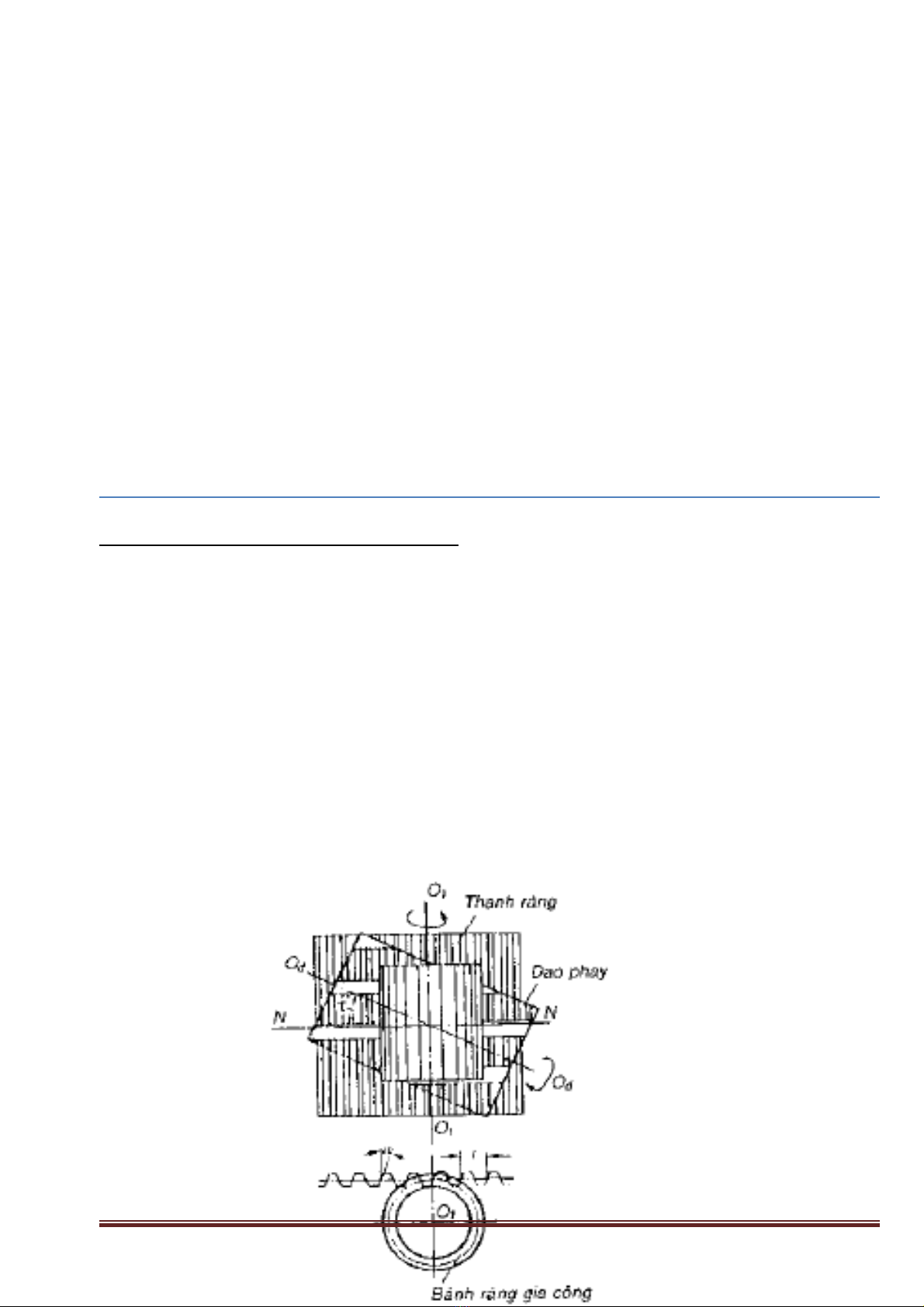
1.1 T ng quan v dao phay lăn răng :ổ ề
Dao phay lăn răng làm vi c theo nguyên lý bao hình có tâm tích. Quá trình hìnhệ
thành profin răng bánh răng b ng dao phay lăn răng t ng t nh quá trình ăn kh pằ ươ ự ư ớ
gi a bánh răng gia công v i tr c vít.Chuy n đng quay c a dao phay lăn răng (tr c vít)ữ ớ ụ ể ộ ủ ụ
quanh tr c c a nó và chuy n đng quay c a phôi bánh răng quanh tr c c a phôi v iụ ủ ể ộ ủ ụ ủ ớ
quan h nh sau: Tr c vít ( dao phay lăn răng ) quay m t vòng thì phôi bánh răng quayệ ư ụ ộ
1/Z1 vòng (Z1 là s răng c a bánh răng c n gia công). Chuy n đng quay c a daoố ủ ầ ể ộ ủ
quanh tr c c a nó đng th i là chuy n đng c t chính. Dao phay lăn răng là m t tr cụ ủ ồ ờ ể ộ ắ ộ ụ
vít có x rãnh d c (th ng là rãnh xo n ) t o thành m t tr c có góc tr c = 0 vàγẻ ọ ườ ắ ạ ặ ướ ướ
rãnh thoát phoi, h t l ng đ t o góc sau.ớ ư ể ạ
HN891 Page 2
1.2 Thi t l p h tr c t a đ khi phay lăn răng:ế ậ ệ ụ ọ ộ
- S dùng 3 h t a đ chính sau:ẽ ệ ọ ộ
- H t a đ Sệ ọ ộ 2 (O2, X2 , Y2 , Z2 ) g n vào bánh răng.ắ
- H t a đ Sệ ọ ộ 1 ( O1, X1, Y1, Z1) đc g n vào thanh răng hay dao ượ ắ phay
lăn răng.
- H t a đ Sệ ọ ộ 0 ( O, X, Y,Z) là h t a đ c đnh. ệ ọ ộ ố ị
Tr c Zụ1 c a h di đng Sủ ệ ộ 1 đc đt trùng v i tr c c a dao phay lăn răng. Tr c Zượ ặ ớ ụ ủ ụ 2 c a ủ
h di đng Sệ ộ 2 đc đt trùng v i tr c c a dao phay lăn răng.ượ ặ ớ ụ ủ
H t a đ áp d ng nh sau:ệ ọ ộ ụ ư
HN891 Page 3
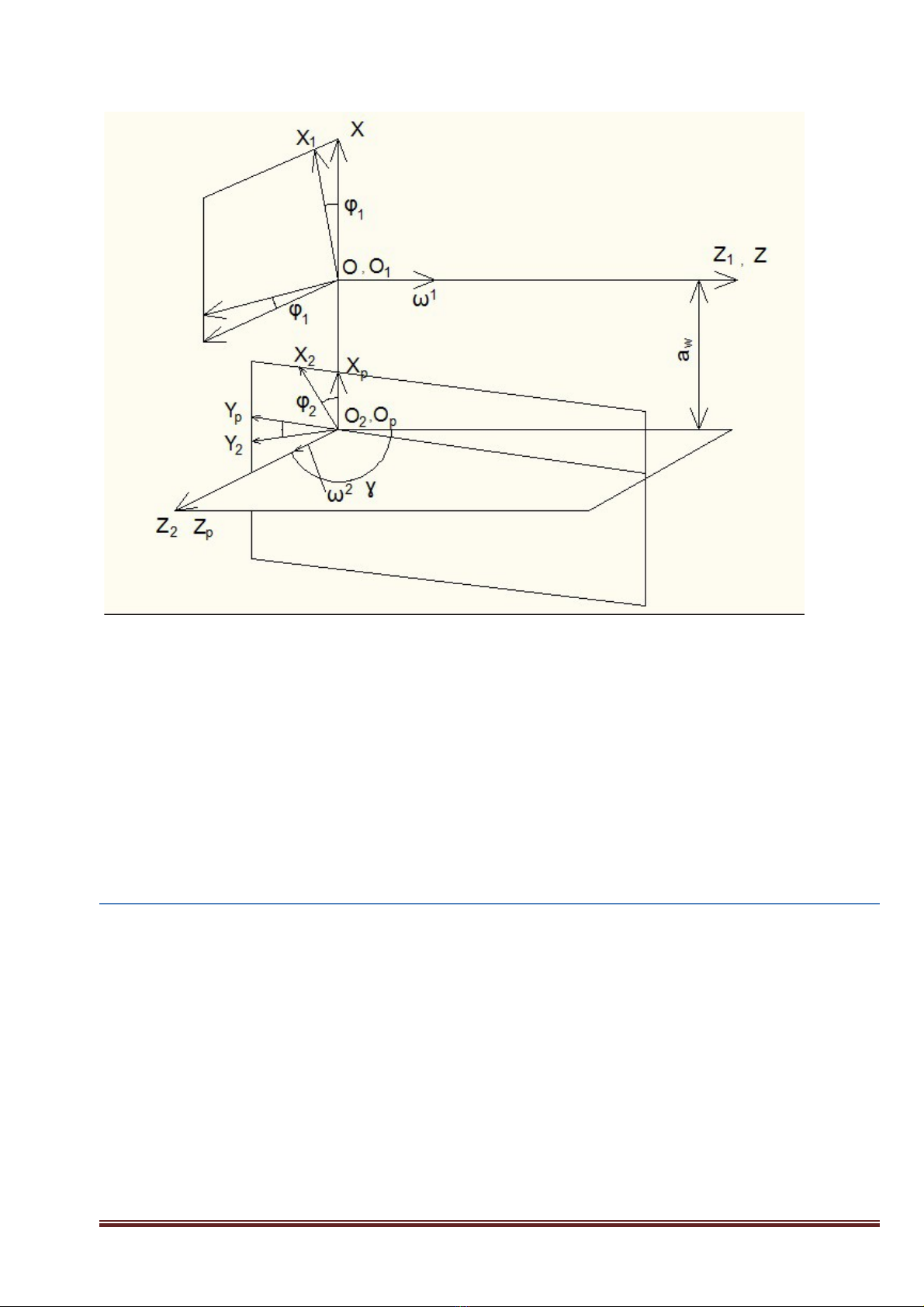
Hình 1: H t a đ áp d ngệ ọ ộ ụ
Ph n II : Thi t l p chuy n đi t a đầ ế ậ ể ổ ọ ộ
Chuy n t h Sể ử ệ 0 ( O, X, Y,Z) đn h Sế ệ 2 (O2, X2 , Y2 , Z2 ): đc th c hi n b i ượ ự ệ ở
hai b c:ướ
- D ch chuy n g c t a đ O đn Oị ể ố ọ ộ ế 2 , quay h t a đ quanh tr c X m t góc ( làγệ ọ ộ ụ ộ
góc gi a hai tr c quay c a b truy n ) sao cho tr c Z đn trùng v i tr c Zữ ụ ủ ộ ề ụ ế ớ ụ p. Ta nh nậ
đc h t a đ trung gian Sượ ệ ọ ộ p (Op, Xp , Yp , Zp ).
- Quay h Sệp quanh Zp m t góc ộ2 nh n đc h Sậ ượ ệ 2 (O2, X2 , Y2 , Z2 ) h g n li nệ ắ ề
v i bánh răng.ớ
HN891 Page 4
Trên hình 1 bi u di n tr ng h p khi quan sát t h ng d ng c a tr c Zể ễ ườ ợ ừ ướ ươ ủ ụ 1 và
Z2, các khâu 1 và 2 quay ng c chi u kim đng h . ượ ề ồ ồ
ng d ng công th c : Ứ ụ ứ M21.r1
Trong đó : r1, r2 là mà tr n c t c a các bán kính vector và c a cùng m t đi mậ ộ ủ ủ ộ ể
trong h Sệ1 và S2.
M01 là ma tr n chuy n đi t h t a đ Sậ ể ổ ừ ệ ọ ộ 1 sang S0.
Mp0 là ma tr n chuy n đi t h t a đ Sậ ể ổ ừ ệ ọ ộ 0 sang Sp.
M2p là ma tr n chuy n đi t h t a đ Sậ ể ổ ừ ệ ọ ộ p sang S2.
M21 là k t qu s chuy n đi gian ti p t h t a đ Sế ả ự ể ổ ế ừ ệ ọ ộ 1 sang S2.
Ta có:
M01 =
Mp0 =
M2p =
Ma tr n Mậ20 khi chuy n t h t a đ Sể ừ ệ ọ ộ 0 sang S2:
M20 = M2p. Mp0 =
V y : ậMa tr n Mậ21 khi chuy n t h t a đ Sể ừ ệ ọ ộ 1 sang S2:
M21 = M2p. Mp0 .M01 =
Bi u th c liên h gi a xể ứ ệ ữ 1, y1, z1 và x2, y2, z2 b ng các ph ng trình:ằ ươ
Chuy n đi ng c t Sể ổ ượ ừ 2 sang S1 :
T ng t nh trên : ươ ự ư
Trong đó M12 là ma tr n ngh ch đo c a ma tr n Mậ ị ả ủ ậ 21 đc xác đnh b i:ượ ị ở
HN891 Page 5