KIỂM TRA 1 TIẾT HỌC KỲ II - MÔN TOÁN 12 (CT Chuẩn)
ĐỀ 1:
Câu 1 : (2 điểm). Tìm phần thực, phần ảo và mô đun của số phức z, biết:
( 2 ) (3 2 )
z i i
Câu 2 : (3 điểm). Thực hiện phép tính :
a)
3 2
(1 2 ) (2 )
z i i
b)
7 2
1
i
z
i
+
2
1
1
i
i
Câu 3 : ( 3 điểm).Giải các phương trình sau trên tập số phức:
a) 2
2 1 0
z z
b) 4 2
6 0
z z
Câu 4: (2 điểm).
a). Trên mặt phẳng tọa độ, hãy tìm tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện
2 2 5 1 2
z i z i
.
b) Tìm số phức z , biết :
3 6 10
z iz i
, với
z
là số phức liên hợp của số phức z .
Tiết 69 ĐÁP ÁN KIỂM TRA 1 TIẾT CHƯƠNG SỐ PHỨC
MÔN TOÁN LỚP 12 năm học 2012 - 2013
CÂU LỜI GIẢI TÓM TẮT ĐỀ 1 ĐIỂM
Câu 1
(2 điểm) z = 1- i . Số phức z có phần thực là 1, phần ảo là -1 và
mô đun bằng
2
0.5 + 0.5
+ 1.0
Câu 2
(3 điểm) a)
3 2
(1 2 ) (2 )
z i i
= 11-2i + 3+4i = 14 + 2i
0.5+ 0.5
+ 0.5
b ) z
7 2
1
i
i
+
2
1
1
i
i
=
( 7 2 )(1 )
(1 )(1 )
i i
i i
+
2
( )
i
=
7 9
2 2
i
0.5+ 0.5
0.5
Câu 3
( 3 điểm)
a) Ta có :
7 0
Phương trình có 2 nghiệm phức là:
1 7
4 4
z i
0.5
0.5 + 0.5
b) Đặt t = z
2
. Khi đó ta có pt : t
2
– t – 6 = 0
3 3
2
2
t z
t
z i
Vậy pt đã cho có 4 nghiệm là :
3; 2
z z i
0.5
0.5
0.5
Câu 4
(2 điểm) Giả sử
z x yi
với , x y
R
và 2
1
i
.
Ta có:
2 2 5 1 2 2 2 2 5 1 2
z i z i x y i x y i
2 2
2 2
2 2 2 5 1 2
x y x y
2 2
3 3 6 24 24 0
x y x y
22
1 4 9
x y
Vậy tập hợp điểm biểu diễn số phức z thỏa mãn điều kiện
0.25
0.25
0.25
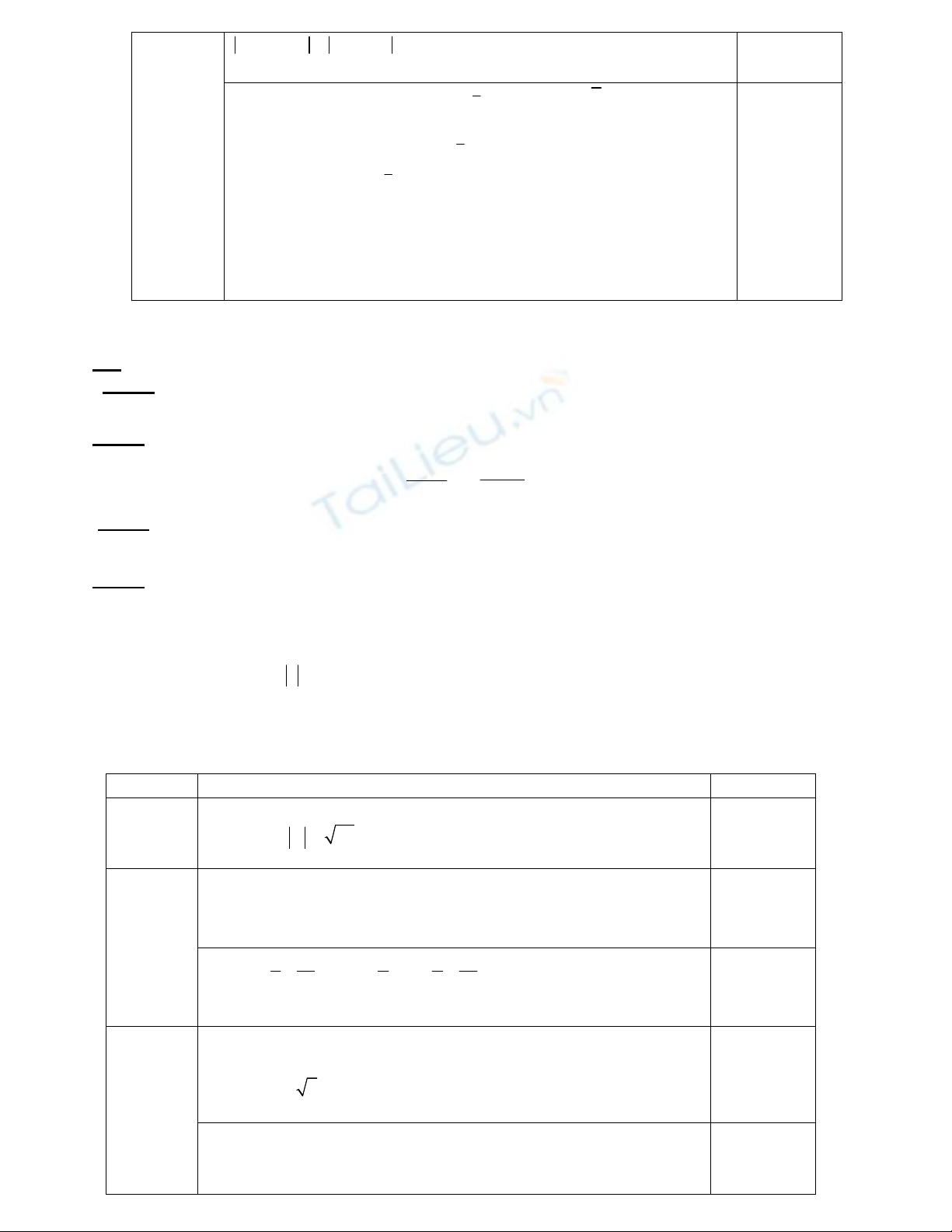
2 2 5 1 2
z i z i
là đường tròn có tâm
1;4
I và bán
kính
3
r
.
0.25
b) Tìm số phức z , biết :
3 6 10
z iz i
, với
z
là số phức
liên hợp của số phức z .
Giả sử
,
z a bi a b R z a bi
Ta có :
3 6 10 3 6 10
z iz i a bi i a bi i
3 6 1
3 10 3
a b a
a b b
Vậy số phức cần tìm là
1 3
z i
0.25
0.5
0.25
ĐỀ 2:
Câu 1 : (2 điểm). Tìm phần thực, phần ảo và mô đun của số phức z, biết:
(2 ) (3 2 )
z i i
.
Câu 2 : (3 điểm).Thực hiện phép tính :
a)
3 2
(1 2 ) (2 )
z i i
b)
7 2
1 2
i
z
i
+
2
1 2
1
i
i
Câu 3 : (3 điểm). Giải các phương trình sau trên tập số phức:
a) 2
2 9 0
z z
b) 4 2
7 10 0
z z
Câu 4 : (2 điểm)
a) Trên mặt phẳng tọa độ, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện :
| 3 | 4
z i
b) Tìm số phức z, biết
5
z
và số phức đó có phần thực gấp hai lần phần ảo.
CÂU LỜI GIẢI TÓM TẮT ĐỀ 2 ĐIỂM
Câu 1
(2 điểm) Z = 5 + i . Số phức Z có phần thực là 5, phần ảo là 1 và mô
đun bằng
26
Z
0.5 + 0.5
+ 1.0
Câu 2
(3 điểm) a)
3 2
(1 2 ) (2 )
z i i
= 11-2i + 3+4i
= 14 + 2i
0.5+ 0.5
0.5
b)
3 16 3 7 17
( 2 )
5 5 2 5 10
Z i i i
0.5+ 0.5
+ 0.5
Câu 3
(3 điểm) a) Ta có :
' 8 0
Phương trình có 2 nghiệm phức là:
1 2 2
z i
0.5
0.5 + 0.5
b) Đặt t = z
2
. Khi đó ta có pt : t
2
– t – 6 = 0
0.5
0.5
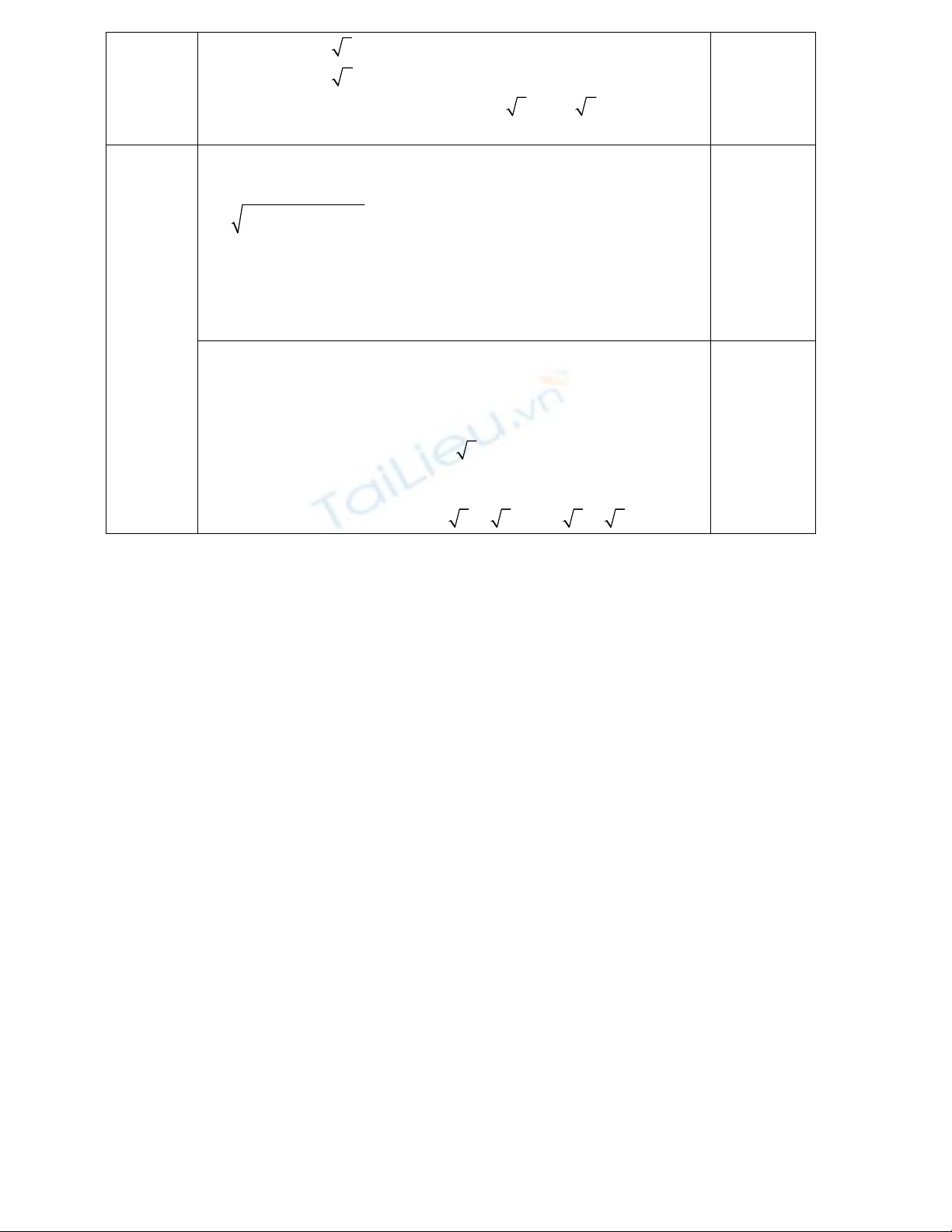
5 5
2
2
t z i
t
z i
Vậy pt đã cho có 4 nghiệm là :
5; 2
z i z i
0.5
Câu 4
(2 điểm) Giả sử
z x yi
với , x y
R
và 2
1
i
.
Theo đề ta có :
| 3 ( 1) | 4
x y i
22
22
3 1 4
3 1 16
x y
x y
Vậy tập hợp điểm biểu diễn số phức z thỏa mãn điều kiện đề
bài là đường tròn có tâm I( - 3; 1) và bán kính
4
r
.
0.25
0.25
0.25
0.25
Giả sử
z x yi
với , x y
R
và 2
1
i
.
Theo đề ta có: 2 2
25
2
x y
x y
2 2
5 25 5
5
2 2 2
y y y
x y x y
x y
Vậy số phức cần tìm là :
2 5 5; 2 5 5
z i z i
0.25
0.5
0.25

KIỂM TRA 1 TIẾT HỌC KỲ II - MÔN TOÁN 12 (CT Chuẩn)
Năm học: 2012-2013
ĐỀ 1
Câu 1: (3 điểm)
Tìm nguyên hàm :
3
) ( 2 )
3
) (cos )
x
a x dx
b x dx
x
Câu 2: (4 điểm)
Tính tích phân:
12
3
0
2
0
) 1
) . os2x.
x
a dx
x
b x c dx
Câu 3: (2 điểm)
Tính diện tích hình phẳng giới hạn bởi các đường :
2
, 3 2
y x y x
.
Câu 4: (1 điểm)
Tính thể tích khối tròn xoay sinh ra do hình phẳng giới hạn bởi elip (E): 2 2
1
9 4
x y
quay quanh trục Ox .
ĐỀ 2
Câu 1: (3 điểm)
Tìm nguyên hàm :
2
) ( 3 )
2
) (sin )
x
a x dx
b x dx
x
Câu 2: (4 điểm)
Tính tích phân:
13
4
0
2
0
) 1
) .sin2x.
x
a dx
x
b x dx
Câu 3: (2 điểm)
Tính diện tích hình phẳng giới hạn bởi các đường :
2
, 4 3
y x y x
.
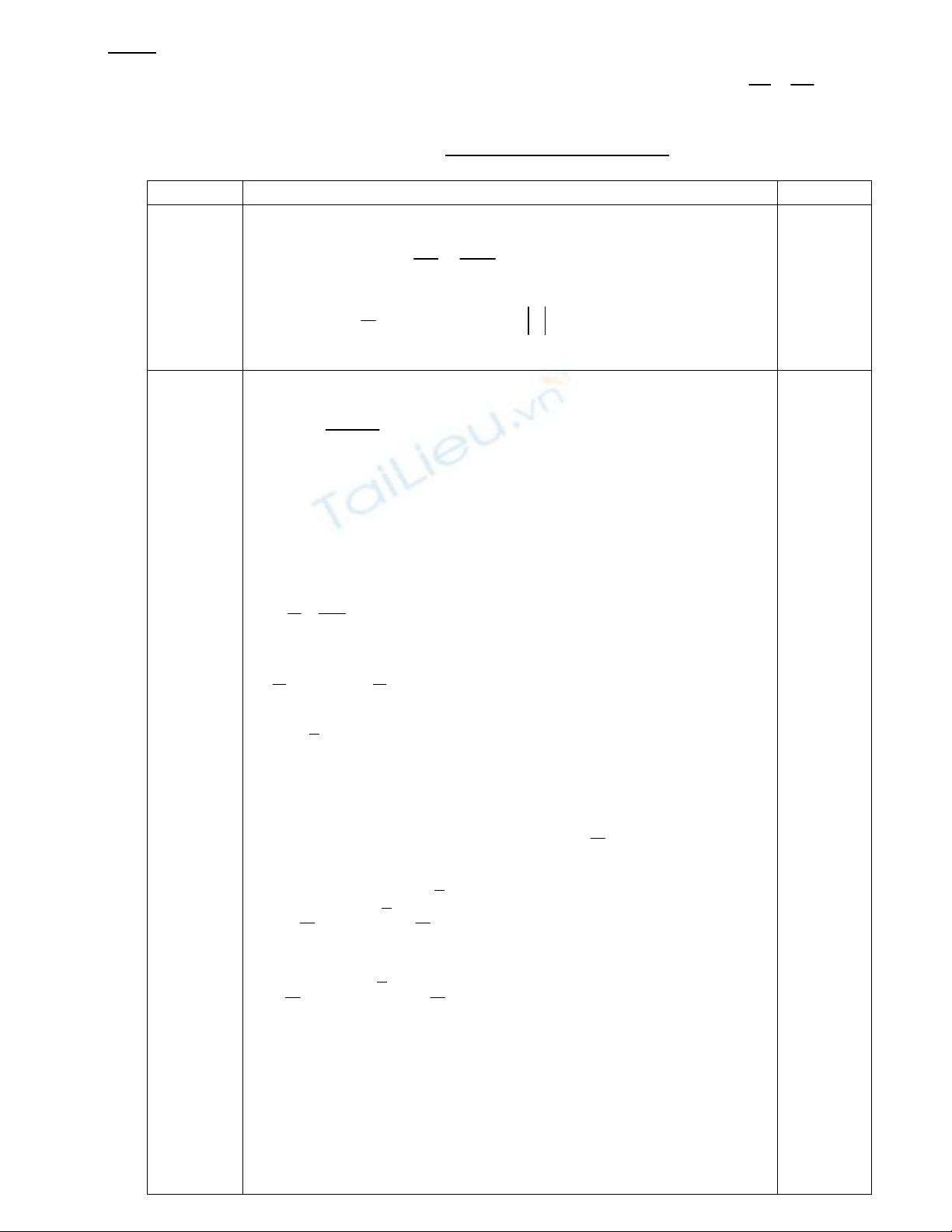
Câu 4: (1 điểm)
Tính thể tích khối tròn xoay sinh ra do hình phẳng giới hạn bởi elip (E): 2 2
1
16 9
x y
quay quanh trục Ox .
ĐÁP ÁN- THANG ĐIỂM
(ĐỀ 1)
Câu Tóm tắt lời giải Điểm
Câu 1
(3 điểm) 4
32
) ( 2 )
4 ln 2
3
) (cos ) sin 3ln
x
xx
a x dx C
b x dx x x C
x
0.75+0.7
5
0.75+0.7
5
Câu 2
(4 điểm)
12
3
0
3 2
2
1
2
1
) A= 1
1 3
0 1
1 2
1
A= 3
1 1
[ ln ] ln2
3 3
x
a dx
x
Dat u x du x dx
x u
x u
du
u
u
2
0
2
2
0
0
2
0
) B= os2x
1
D¨t u=x;dv=cos2xdx => du=dx; v= sin2
2
1 1
[ sin2 ] sin2
2 2
1 1
[ 2 ]
4 2
b xc dx
x
B x xdx
cox x
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
















