intTypePromotion=1
zunia.vn Tuyển sinh 2024 dành cho Gen-Z zunia.vn zunia.vn
ADSENSE
 » 
 » 

Bài giảng Cơ học kỹ thuật (Phần Tĩnh học): Chương 5 - Nguyễn Quang Hoàng

Chia sẻ: _ _ | Ngày: | Loại File: PDF | Số trang:10

Thêm vào BST
Báo xấu
13
lượt xem 2
download
 
  Download Vui lòng tải xuống để xem tài liệu đầy đủ

Bài giảng "Cơ học kỹ thuật (Phần Tĩnh học): Chương 5 - Trọng tâm vật rắn" được biên soạn với các nội dung chính sau: Trọng tâm của hệ chất điểm; Trọng tâm của vật rắn; Các công thức Pappus và Guldinus; Xác định trọng tâm bằng thực nghiệm. Mời các bạn cùng tham khảo bài giảng!

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài giảng Cơ học kỹ thuật (Phần Tĩnh học): Chương 5 - Nguyễn Quang Hoàng

  1. Chương 5. Trọng tâm vật rắn – Center of Gravity Cơ học kỹ thuật: TĨNH HỌC 5 Chương Engineering Mechanics: STATICS Trọng tâm vật rắn Nguyễn Quang Hoàng Bộ môn Cơ học ứng dụng Chương 5. Trọng tâm vật rắn – Center of Gravity -2- Nội dung • Trọng tâm của hệ chất điểm • Trọng tâm của vật rắn  Công thức xác định  Trọng tâm của các vật rắn đồng chất  Trọng tâm của các vật rắn đồng chất đối xứng  Trọng tâm của các vật ghép • Các công thức Pappus và Guldinus • Xác định trọng tâm bằng thực nghiệm  Phương pháp vẽ xác định trọng tâm của tấm phẳng dạng chữ L.  Phương pháp treo vật - phương pháp đường dọi.  Phương pháp cân. Nguyễn Quang Hoàng - Department of Applied Mechanics-SME Chương 5. Trọng tâm vật rắn – Center of Gravity -3- Mở đầu b c ?Qmax P ?Wmax A B a G Nguyễn Quang Hoàng - Department of Applied Mechanics-SME 1
  2. Chương 5. Trọng tâm vật rắn – Center of Gravity -4- Trọng tâm của hệ chất điểm z Từ điều kiện tương đương về mô men đối với các trục, ta nhận được công thức Wn n W G W  k W1 k 1 W2 zG  n  n O y my (W )   m (W )  x W   x W y k G k k xG k 1 k 1 yG  n  n mx (W )   m (W )  y W x k G   ykWk x k 1 k 1 y Quay hệ cùng với hệ trục tọa độ 90o quanh W1 trục x hoặc y G  n  n mx (W )   m (W )  z W  W z x k G k k W2 k 1 k 1 Wn Công thức xác định vị trí trọng tâm G O z xG  x kWk  ykWk  z kWk zG xG  , yG  , zG  Wk Wk Wk x Nguyễn Quang Hoàng - Department of Applied Mechanics-SME Chương 5. Trọng tâm vật rắn – Center of Gravity -5- Trọng tâm của vật rắn: công thức xác định Trọng lượng của vật z W   dW  mg dV G=C dW Vị trí trọng tâm của vật W   z my (W )  xGW   my (dW )   xdW  zG O y x xG y    xdW 1  xG  W  yG x 1 1 1 W  W  W  xG   xdW , yG   ydW , zG   zdW Khi gia tốc trọng trường g = const, trọng tâm G và khối tâm C của vật trùng nhau. Nguyễn Quang Hoàng - Department of Applied Mechanics-SME Chương 5. 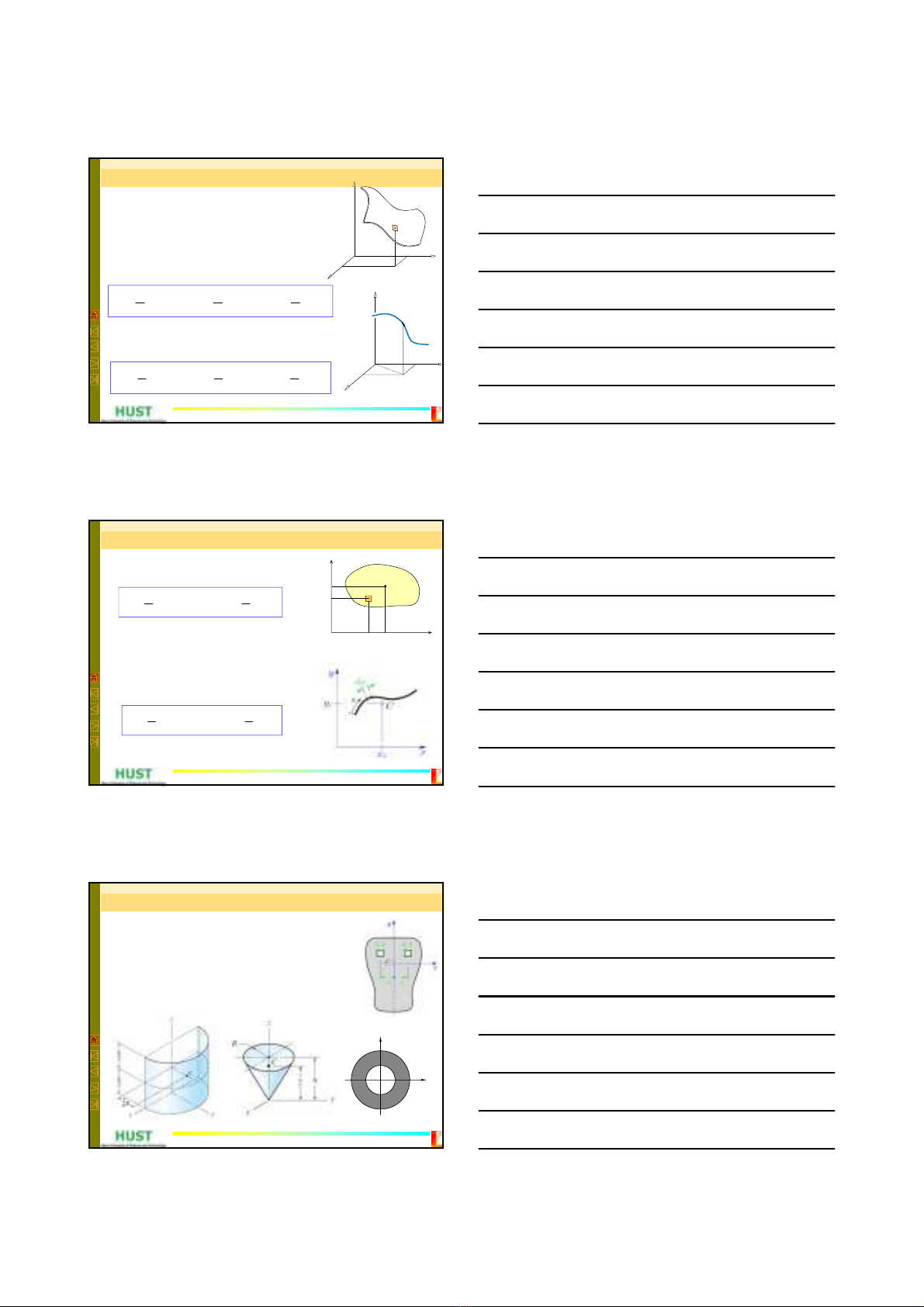Trọng tâm vật rắn – Center of Gravity -6- Trọng tâm của các vật rắn đồng chất Đối với vật thể đồng chất dạng khối dW  g  dm  g    dV , g [m/ s2 ],  [kg/ m 3 ] z g  const,   const V G dV O z y Trọng tâm của vật thể đồng chất dạng khối (3D) x x y 1 1 1 xG  V  V  , xdV yG  V V  , ydV zG  V V  zdV Nguyễn Quang Hoàng - Department of Applied Mechanics-SME 2
  3. Chương 5. Trọng tâm vật rắn – Center of Gravity -7- Trọng tâm của các vật rắn đồng chất Đối với vật thể đồng chất dạng tấm vỏ z A dW  g  dm  g    dA, dA g [m/ s2 ],  [kg/ m2 ] z Đối với vật thể dạng tấm (vỏ) bề dày không đổi x y (phẳng, cong) y x 1 1 1 A A xG   , yG   ydA xdA  , zG   zdA  z L A A A A dL Đối với vật thể dạng thanh (dây) diện tích mặt cắt không đổi (phẳng, cong) z 1 1 1 x y L L xG   , yG   ydL xdL  , zG   zdL  y L L L L x Nguyễn Quang Hoàng - Department of Applied Mechanics-SME Chương 5. Trọng tâm vật rắn – Center of Gravity -8- Trọng tâm của các vật rắn đồng chất Đối với tấm phẳng (2D) y yC C dA 1 1 y A A A A xC   , xdA yC   ydA O x xC x Đối với vật thể dạng thanh (dây) diện tích mặt cắt không đổi (phẳng) 1 1 L L L L xC   , xds yC   yds Nguyễn Quang Hoàng - Department of Applied Mechanics-SME Chương 5. 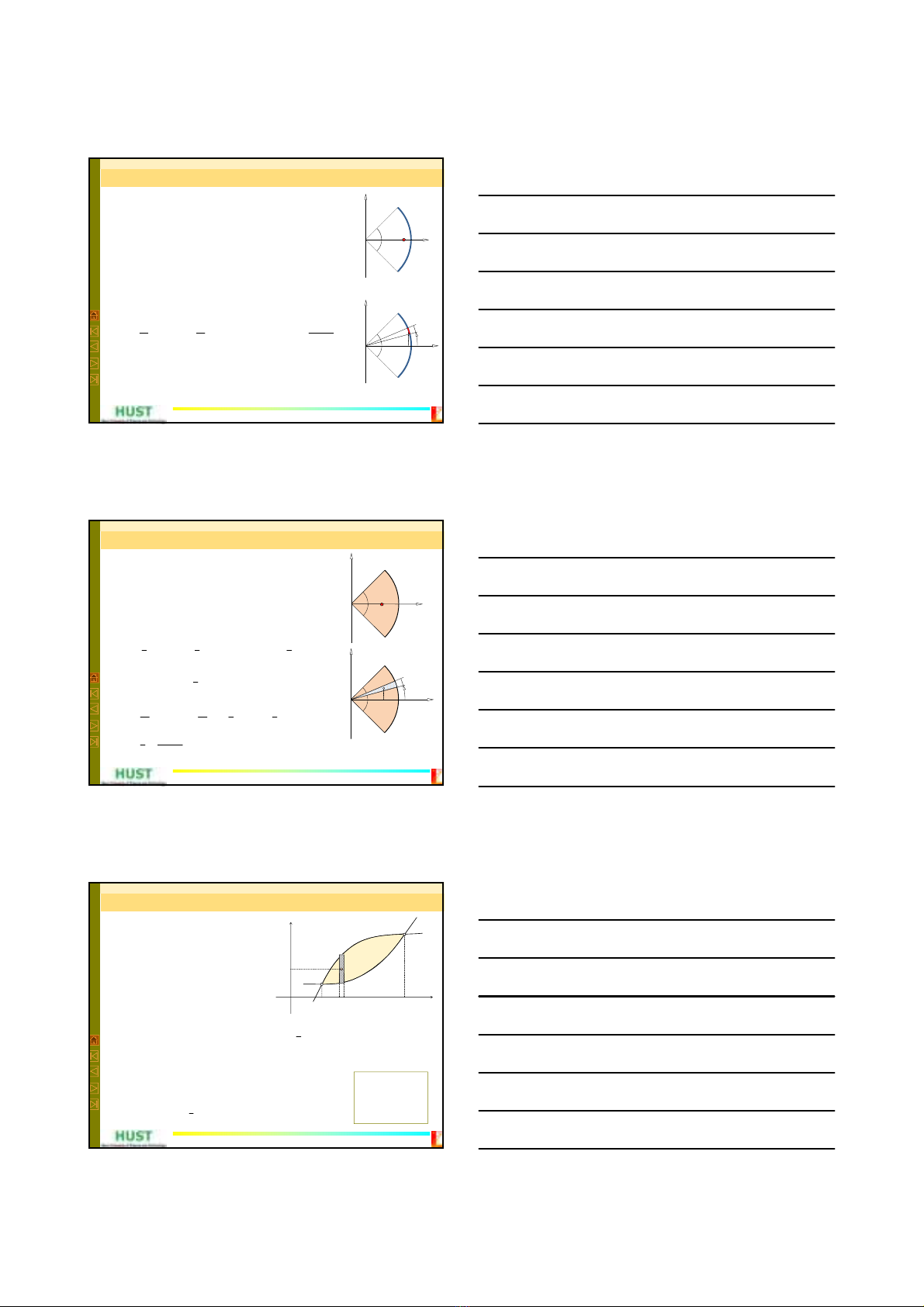Trọng tâm vật rắn – Center of Gravity -9- Trọng tâm của các vật rắn đồng chất đối xứng 1. Nếu vật rắn có một mặt phẳng (trục hoặc điểm) đối xứng, thì trọng tâm của vật nằm trên mặt phẳng (trục hoặc điểm) đối xứng đó. 2. Nếu vật có một số mặt phẳng (trục) đối xứng, trọng tâm của vật rắn nằm trên giao của các mặt phẳng (trục) đối xứng đó. y O x Nguyễn Quang Hoàng - Department of Applied Mechanics-SME 3
  4. Chương 5. Trọng tâm vật rắn – Center of Gravity -10- Xác định trọng tâm bằng công thức tích phân Ví dụ. Xác định trọng tâm của dây cung tròn bán y B kính R, góc mở 2α. L Lời giải a Dựng hệ Oxy, x là trục đối xứng  yC = 0. O a C x Chọn phân tố chiều dài dL (xác định bởi , d) R a dL = Rd j, L= ò -a Rd j = 2aR A y x = R cos j B dL 1 1 a sin a dj xC = L ò  = xdL L ò-a R cos jRdj = R a j O x x Trường hợp nửa đường tròn α = π/2 R A xC = 2R / p < R Nguyễn Quang Hoàng - Department of Applied Mechanics-SME Chương 5. Trọng tâm vật rắn – Center of Gravity -11- Xác định trọng tâm bằng công thức tích phân Ví dụ. Xác định trọng tâm của tấm hình quạt bán y kính R, góc mở 2α. A Lời giải  Dựng hệ Oxy, x là trục đối xứng  yC = 0. Chọn O  x phân tố diện tích dA dạng tam giác, (xác định bởi , d) R dA = 21 RRd j = 21 R 2d j, x = 23 R cos j y A a dA dj ò dA = ò 2 A= 1 R ⋅ Rd j = aR -a 2 j O 1 1 a a x x Aò xC =  = ò 23 R cos j 21 RRd j xdA R A -a sin a = 23 R a Trh nửa đĩa tròn, α = π/2 xC = 4R / 3p Nguyễn Quang Hoàng - Department of Applied Mechanics-SME Chương 5. Trọng tâm vật rắn – Center of Gravity -12- Xác định trọng tâm bằng công thức tích phân Trọng tâm của tấm phẳng xác định y bởi hai hàm y1(x) và y2(x) y2 = f2(x) 1. Xác định miền giới hạn của tấm d y1(x) = y2(x)  x1 & x2 y A y1 = f1(x) 2. Chọn phân tố diện tích dạng dx hình chữ nhật ở vị trí x và có bề O x1 x2 x x rộng dx dA = [f2 (x ) - f1(x )]dx , x = x , y = 21 [f2 (x ) + f1(x )] x2 3. Tính các tích phân A = ò dA = ò x1 [f2 (x ) - f1 (x )]dx x2 xC = A-1 ò xdA  ò xdA  = òx1 x [f2 (x ) - f1 (x )]dx x2 ò ydA  = òx1 1 2 [f2 (x ) + f1 (x )][f2 (x ) - f1 (x )]dx yC = A-1 ò ydA  Nguyễn Quang Hoàng - Department of Applied Mechanics-SME 4
  5. Chương 5. Trọng tâm vật rắn – Center of Gravity -13- Xác định trọng tâm bằng công thức tích phân y Ví dụ: Xác định diện tích và trọng tâm của tấm y = 9– x2 phẳng cho trên hình bên. HD 9m f2 (x ) = 9 - x 2 , f1(x ) = 0 O x dA = (9 - x 2 )dx , x = x , y = 21 y = 21 (9 - x 2 ) 3m y 3 y = 9– x2 A = ò dA = ò 0 (9 - x 2 )dx = 18 m2 dA 9m C 1 1 3 A A 0 xC    xdA x (9  x 2 )dx  1,125 m y dx 1 1 31 yC   ydA A 0 2   (9  x 2 )(9  x 2 )dx  5, 4 m O x 3 x A Nguyễn Quang Hoàng - Department of Applied Mechanics-SME Chương 5. Trọng tâm vật rắn – Center of Gravity -14- Xác định trọng tâm bằng công thức tích phân Ví dụ. Xác định vị trí trọng tâm tấm phẳng rộng 2a cao h, đường bao là parabol. HD. Dựng hệ Oxy, với trục y là trục đối xứng: xC = 0. Chọn phân tố diện tích dA song song trục x, dA = 2x dy. Khoảng cách từ phân tố đến trục x xác định từ phương trình của parabol Nguyễn Quang Hoàng - Department of Applied Mechanics-SME Chương 5. Trọng tâm vật rắn – Center of Gravity -15- Xác định trọng tâm bằng công thức tích phân yC = ò ydA Cần tính yC theo công thức ò dA h h a 2y 2 a 2y 3 4 A= ò dA = ò 2xdy = 2 ò 0 h dy = 2 ⋅ 3 h = 3 ah 0 h h a 2y 2 a 2y 5 4 ò ydA  = 2ò 0 y h dy = 2 ⋅ 5 h = ah 2 5 0 Thay vào công thức tính yC cho ta kết qủa yC = ò ydA  3 = h ò dA 5 Nguyễn Quang Hoàng - Department of Applied Mechanics-SME 5
  6. Chương 5. Trọng tâm vật rắn – Center of Gravity -16- Trọng tâm của vật ghép – composite bodies Nếu vật rắn được ghép từ nhiều phần, trọng z tâm của nó được xác định theo G1 G3  x kWk  ykWk  z kWk G2 xG  , yG  , zG  Wk Wk Wk O y Wk , x k , yk , z k trọng lượng và tọa độ trọng tâm của phần ghép thứ k. x Lưu ý: 1. Đối với vật rắn đồng chất: Wk  Vk , Ak , Lk 2. Phần khuyết nằm trong vật có thể coi như có trọng lượng âm. 3. Nếu các Gk nằm trên một đường (mặt) thì G nằm trên đường (mặt) đó. Nguyễn Quang Hoàng - Department of Applied Mechanics-SME Chương 5. Trọng tâm vật rắn – Center of Gravity -17- Trọng tâm của vật ghép – composite bodies Vật ghép đồng chất Vật ghép đồng chất Vật ghép đồng chất dạng khối 3D dạng tấm 2D dạng dây (thanh) Wk  Vk Wk  kVk Wk  Ak Wk  k Ak Wk  Lk Wk  k Lk  x kVk  x k kVk xG  , xG  ,  x k Ak  x k k Ak Vk  kVk xG  , xG  ,  x k Lk  x k k Lk  ykVk  yk kVk  Ak  k Ak xG  , xG  , yG  yG   Lk  k Lk , ,  yk Ak  yk k Ak Vk  kVk yG  , yG  ,  yk Lk  yk k Lk  z kVk  z k kVk  Ak  k Ak yG  , yG  , zG  zG   Lk  k Lk  z k Ak  z k k Ak Vk  kVk zG  zG   z k Lk  z k k Lk  Ak  k Ak zG  zG   Lk  k Lk Gi G1 G2 Nguyễn Quang Hoàng - Department of Applied Mechanics-SME Chương 5. Trọng tâm vật rắn – Center of Gravity -18- Trọng tâm của vật ghép – composite bodies y Vi dụ 1. Phần 1. Tam giác b + Phần 2. Đĩa tròn a/2 r - (trọng lượng âm) a/2 Phần 3. Vuông a/2 a/2 x k Area [m2] xk [m] yk [m] xkAk [m3] ykAk [m3] Trọng tâm của tấm 1 1 ab a /3 a b /3 ? ? 2  x k Ak 2 ? ? xC   ?,  12  r 2 a /2 a /2  Ak 3 a2 a/2 a/2 ? ?  yk Ak Ak xkAk ykAk yC  ?  Ak Nguyễn Quang Hoàng - Department of Applied Mechanics-SME 6
  7. Chương 5. Trọng tâm vật rắn – Center of Gravity -19- Trọng tâm của vật ghép – composite bodies Ví dụ 2. Một lập phương nhỏ cạnh 2a được cắt bỏ từ lập phương lớn cạnh 4a (Hình a) a) Xác định trọng tâm của phần còn lại. b) Xác định trọng tâm của lập phương lớn, nếu bù chỗ khuyết bằng một lập phương nhỏ làm bằng vật liệu khác có khối lượng riêng 2 = 21. (Hình b). Nguyễn Quang Hoàng - Department of Applied Mechanics-SME Chương 5. Trọng tâm vật rắn – Center of Gravity -20- Trọng tâm của vật ghép – composite bodies Trong cả hai trường hợp ta coi vật thể như được ghép từ nhiều vật dạng hôp chữ nhật. a) PA1. Coi vật thể đồng chất được ghép từ 3 vật thể dạng hộp chữ nhật (cùng khối lượng riêng 1). Lập được bảng, tính và nhận được kết quả Nguyễn Quang Hoàng - Department of Applied Mechanics-SME Chương 5. Trọng tâm vật rắn – Center of Gravity -21- Trọng tâm của vật ghép – composite bodies a) PA2. Coi vật thể đồng chất được ghép từ 2 lập phương cạnh 4a và cạnh 2a, phần cạnh 2a coi như có trọng lượng âm. Lập được bảng, tính và nhận được kết quả Nguyễn Quang Hoàng - Department of Applied Mechanics-SME 7
  8. Chương 5. Trọng tâm vật rắn – Center of Gravity -22- Trọng tâm của vật ghép – composite bodies b) Vật thể được ghép từ 2 phần (phần 1 đã biết từ câu a, khối lượng riêng 1 ) và phần 2 là lập phương cạnh 2a, khối lượng riêng 2 = 21 : Lập được bảng, tính và nhận được kết quả, Nguyễn Quang Hoàng - Department of Applied Mechanics-SME Chương 5. Trọng tâm vật rắn – Center of Gravity -23- Các công thức Pappus và Guldinus Định lý 1. Diện tích của mặt tròn xoay sinh ra bởi đường cong phẳng L quay quanh một trục  đồng phẳng không cắt nó bằng tích chiều dài đường cong với chiều dài đường tròn tạo ra bởi trọng tâm của đường cong quay quanh trục . A  2 yC L  2 yL y C dL yC y x  L dA  2 r  dL  2 y  dL A   dA   2 y  dL  2 yC L Nguyễn Quang Hoàng - Department of Applied Mechanics-SME Chương 5. Trọng tâm vật rắn – Center of Gravity -24- Các công thức Pappus và Guldinus Định lý 2. Thể tích khối tròn xoay sinh ra bởi hình phẳng quay quanh trục đồng phẳng  không cắt nó bằng tích của diện tích hình phẳng và chiều dài đường tròn tạo ra bởi trọng tâm của hình phẳng quay quanh trục đó. V  2 yC A  2 yA dA y C y yC x  dV  2 r  dA  2 y  dA V   dV   2 y  dA  2 yC A  2 rC A Nguyễn Quang Hoàng - Department of Applied Mechanics-SME 8
  9. Chương 5. Trọng tâm vật rắn – Center of Gravity -25- Các công thức Pappus và Guldinus Ví dụ 1. Tính diện tích tang trống y y B L L L  2 R, a xC O O x a x d  xC  R 1 sin  R A sin  A  2 dL  2 R 2 R  4 R 2 sin   z    / 2  A  4 R 2 a a r Ví dụ 2. Tính thể tích hình xuyến rC = r, A = a 2  V = 2prC A = 2pra 2 Nguyễn Quang Hoàng - Department of Applied Mechanics-SME Chương 5. Trọng tâm vật rắn – Center of Gravity -26- Xác định trọng tâm bằng thực nghiệm Phương pháp vẽ xác định trọng tâm của tấm phẳng dạng chữ L B A B E E C D A D Nguyễn Quang Hoàng - Department of Applied Mechanics-SME Chương 5. Trọng tâm vật rắn – Center of Gravity -27- Xác định trọng tâm bằng thực nghiệm Phương pháp đường dọi xác định trọng tâm tấm phẳng B A A B n C B A a) m b) n c) Nguyễn Quang Hoàng - Department of Applied Mechanics-SME 9
  10. Chương 5. Trọng tâm vật rắn – Center of Gravity -28- Xác định trọng tâm bằng thực nghiệm Phương pháp cân đo l l x N2 x N1 N cân P cân 2 P cân 1 Sử dụng hai cân (cân 1 lần) Sử dụng một cân (hai lần cân) Cân hai đầu xác định được N1 Cân lần 1 (cả vật) xác định P và N2, P = N1 + N2 Cân lần 2 (một đầu), xác định N Đo L Đo L x  lN 2 / P x  lN / P  lN 2 / (N 1  N 2 ) Nguyễn Quang Hoàng - Department of Applied Mechanics-SME Chương 5. Trọng tâm vật rắn – Center of Gravity -29- Tóm tắt nội dung • Trọng tâm của hệ chất điểm • Trọng tâm của vật rắn  Công thức xác định  Trọng tâm của các vật rắn đồng chất/đối xứng  Trọng tâm của các vật ghép • Các công thức Pappus và Guldinus  Tính diện tích mặt tròn xoay, tính thể tích hình xuyến • Xác định trọng tâm bằng thực nghiệm  Phương pháp vẽ xác định trọng tâm của tấm phẳng dạng chữ L.  Phương pháp treo vật - phương pháp đường dọi.  Phương pháp cân. Nguyễn Quang Hoàng - Department of Applied Mechanics-SME 10
ADSENSE

CÓ THỂ BẠN MUỐN DOWNLOAD

THÔNG TIN
TRỢ GIÚP
HỖ TRỢ KHÁCH HÀNG
Theo dõi chúng tôi

Chịu trách nhiệm nội dung:

Nguyễn Công Hà - Giám đốc Công ty TNHH TÀI LIỆU TRỰC TUYẾN VI NA

LIÊN HỆ

Địa chỉ: P402, 54A Nơ Trang Long, Phường 14, Q.Bình Thạnh, TP.HCM

Hotline: 093 303 0098

Email: support@tailieu.vn

Giấy phép Mạng Xã Hội số: 670/GP-BTTTT cấp ngày 30/11/2015 Copyright © 2022-2032 TaiLieu.VN. All rights reserved.

 

Đồng bộ tài khoản
2=>2