
PHÂN PHỐI CHƯƠNG TRÌNH
45 TIẾT LÝ THUYẾT + 30 TIẾT BÀI TẬP
Ch 1. GIỚI HẠN CỦA DÃY SỐ (BT)
Ch 2. GIỚI HẠN CỦA HÀM SỐ MỘT BIẾN
Ch 3. ĐẠO HÀM VÀ VI PHÂN HÀM MỘT BIẾN
Ch 4. PHÉP TÍNH TÍCH PHÂN CỦA HÀM 1 BIẾN
Ch 5. PHƯƠNG TRÌNH VI PHÂN THƯỜNG
lOMoARcPSD|16991370
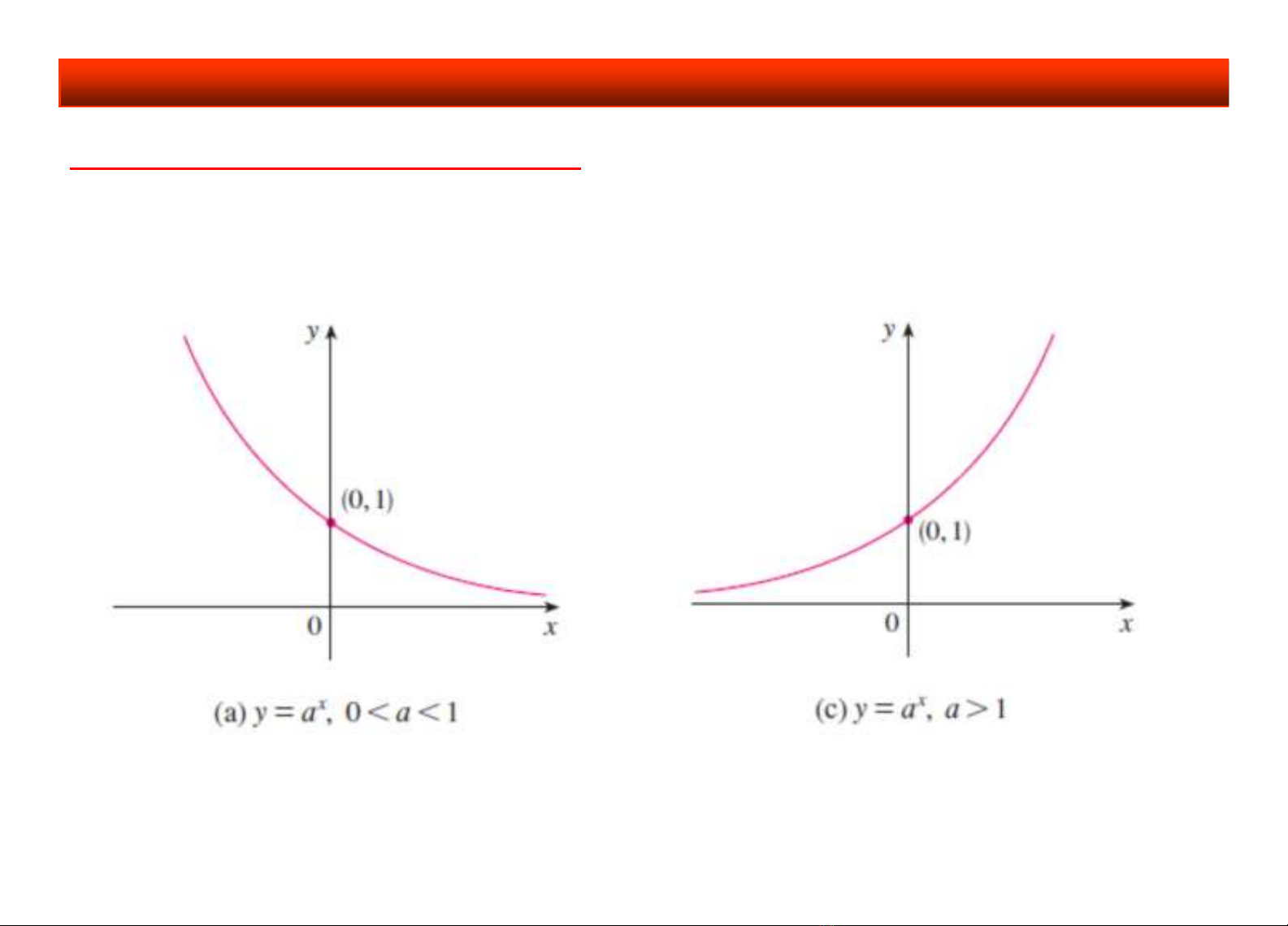
Nhắc lại các hàm đã học
• Hàm nghịch biến
lim 0, lim
x x
x x
a a
• Hàm đồng biến
lim , lim 0
x x
x x
a a
Bài 1. Hàm số một biến
1. Hàm số mũ:
, 0, 1
x
y a a a
MXD:
; MGT :(0; )D
lOMoARcPSD|16991370
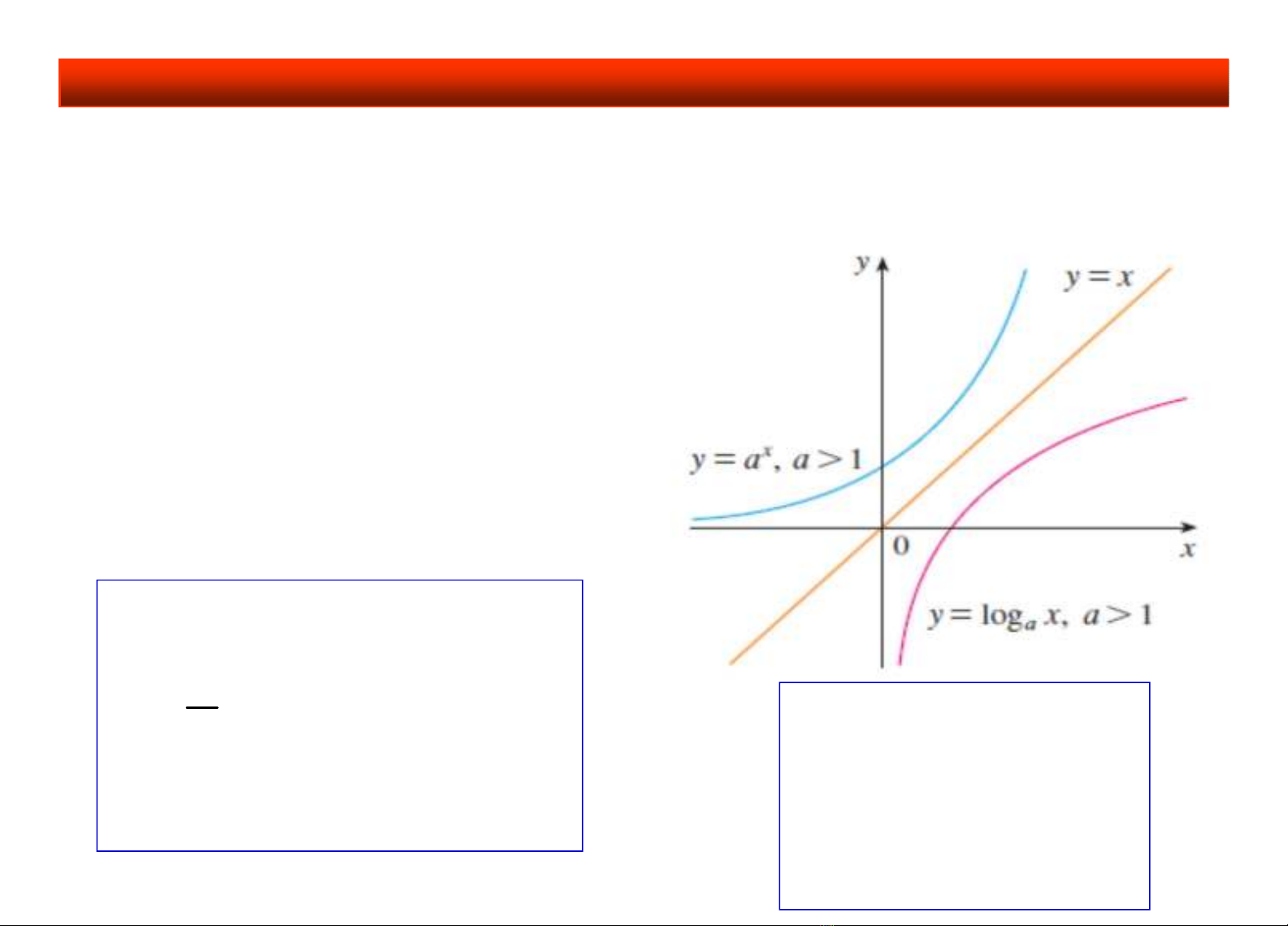
a>1: Hàm đồng biến
Bài 1. Hàm số một biến
2. Hàm số logarit:
log , 0, 1
a
y x a a
MXD:
(0; ); MGT :D
log
log
log ( ) ,
, 0
a
y
a
x
a
x
y x x a
a x x
a x x
log ( . ) log log
log log log
log ( ) log ,
a a a
a a a
r
a a
x y x y
x
x y
y
x r x r R
Tính chất:
0<a<1: Hàm nghịch biến
lOMoARcPSD|16991370




























