Baøi giaûng NGUYEÂN LYÙ MAÙY Chöông 5: Caân baèng maùy
Bm. Thieát keá maùy TS. Buøi Troïng Hieáu
- 71 -
Chöông 5
CAÂN BAÈNG MAÙY
5.1. ÑAÏI CÖÔNG
1. Muïc ñích caân baèng maùy
- Khi laøm vieäc, caùc boä phaän chuyeån ñoäng cuûa maùy seõ sinh ra löïc quaùn tính. Löïc quaùn tính
laøm taêng aùp löïc khôùp ñoäng daãn ñeán taêng ma saùt ôû caùc khôùp, laøm giaûm hieäu suaát của maùy,
maøi moøn nhanh caùc chi tieát maùy, ... Löïc quaùn tính phuï thuoäc vò trí cuûa cô caáu vaø thay ñoåi theo
chu kyø laøm vieäc cuûa maùy, neân aùp löïc khôùp ñoäng cuõng phuï thuoäc vaøo löïc quaùn tính vaø thay
ñoåi theo chu kyø. Ta goïi aùp löïc naøy laø phaûn löïc ñoäng phuï ñeå phaân bieät vôùi aùp löïc khoâng ñoåi do
caùc taûi troïng tónh gaây neân.
- Vì bieán thieân coù chu kyø neân löïc quaùn tính laø nguyeân nhaân chuû yeáu gaây ra hieän töôïng rung
ñoäng treân maùy vaø moùng maùy. Hieän töôïng rung ñoäng naøy laøm giaûm ñoä chính xaùc cuûa maùy,
giaûm chaát löôïng saûn phaåm, gaây oàn aøo, aûnh höôûng xaáu ñeán ñieàu kieän laøm vieäc, giaûm tuoåi thoï
cuûa maùy, laøm hö haïi caùc thieát bò, nhaø cöûa xung quanh, ... Khi taàn soá rung xaáp xæ taàn soá dao
ñoäng rieâng cuûa maùy thì bieân ñoä rung taêng raát lôùn (hieän töôïng coäng höôûng) coù theå phaù vôõ maùy.
Vì vaäy ta phaûi khöû toaøn boä hay moät phaàn löïc quaùn tính ñeå noù khoâng truyeàn vaøo khôùp ñoäng vaø
moùng maùy, loaïi tröø nguoàn goác gaây ra rung ñoäng. Ñaây chính laø muïc ñích cuûa vieäc caân baèng maùy.
2. Noäi dung caân baèng maùy
Caân baèng maùy laø moät vieäc phöùc taïp, trong phaïm vi chöông trình chuùng ta chæ khaûo saùt hai
vaán ñeà cô baûn sau:
- Caân baèng vaät quay: phaân boá laïi khoái löôïng vaät quay ñeå khöû ñi löïc quaùn tính vaø moment
löïc quaùn tính cuûa caùc vaät quay. Ví duï: caân baèng baùnh raêng, baùnh ñaø, caùnh quaït, truïc tuabin, …
- Caân baèng cô caáu: phaân boá laïi khoái löôïng caùc khaâu cuûa cô caáu ñeå khöû ñi löïc quaùn tính vaø
moment löïc quaùn tính khi cô caáu laøm vieäc daãn ñeán khöû aùp löïc do chuùng gaây ra treân moùng
maùy, neân vaán ñeà naøy coøn ñöôïc goïi laø caân baèng treân moùng hay caân baèng treân neàn.
5.2. CAÂN BAÈNG VAÄT QUAY
1. Caân baèng vaät quay coù beà daøy nhoû (Caân baèng tónh)
a). Nguyeân taéc caân baèng
Ñònh nghóa: Vaät quay ñöôïc goïi laø coù beà daøy nhoû khi tæ soá kích thöôùc doïc truïc L vaø
kích thöôùc höôùng truïc D nhoû tôùi möùc coù theå coi toaøn boä khoái löôïng vaät quay phaân boá
treân moät maët phaúng vuoâng goùc vôùi truïc quay (hình 5.1). Ví duï: caùc chi tieát nhö baùnh
raêng, baùnh ñaø, … khi quay vôùi vaän toác khoâng cao thì ñöôïc xem nhö thuoäc loaïi naøy.
Baøi giaûng NGUYEÂN LYÙ MAÙY Chöông 5: Caân baèng maùy
Bm. Thieát keá maùy TS. Buøi Troïng Hieáu
- 72 -
L
D
Hình 5.1
Nguyeân taéc caân baèng:
- Neáu vaät coù beà daøy nhoû maát caân baèng thì khi quay seõ sinh ra löïc quaùn tính. Vì löïc quaùn
tính vaø khoái taâm cuûa vaät cuøng naèm trong moät maët phaúng (khoâng truøng nhau) neân khi thu
goïn löïc quaùn tính veà khoái taâm seõ ñöôïc moät vector löïc quaùn tính 0≠
qt
P vaø vector
moment löïc quaùn tính 0=
qt
M. Tröôøng hôïp maát caân baèng naøy ñöôïc goïi laø maát caân
baèng tónh vì coù theå phaùt hieän maát caân baèng ôû traïng thaùi tónh.
- Do ñoù, nguyeân taéc caân baèng trong tröôøng hôïp naøy laø phaân boá laïi khoái löôïng trong moät
maët phaúng sao cho khoái taâm cuûa vaät veà truøng vôùi taâm quay ñeå khöû löïc quaùn tính sinh ra
khi vaät quay ( 0=
qt
P → vaät ñöôïc caân baèng).
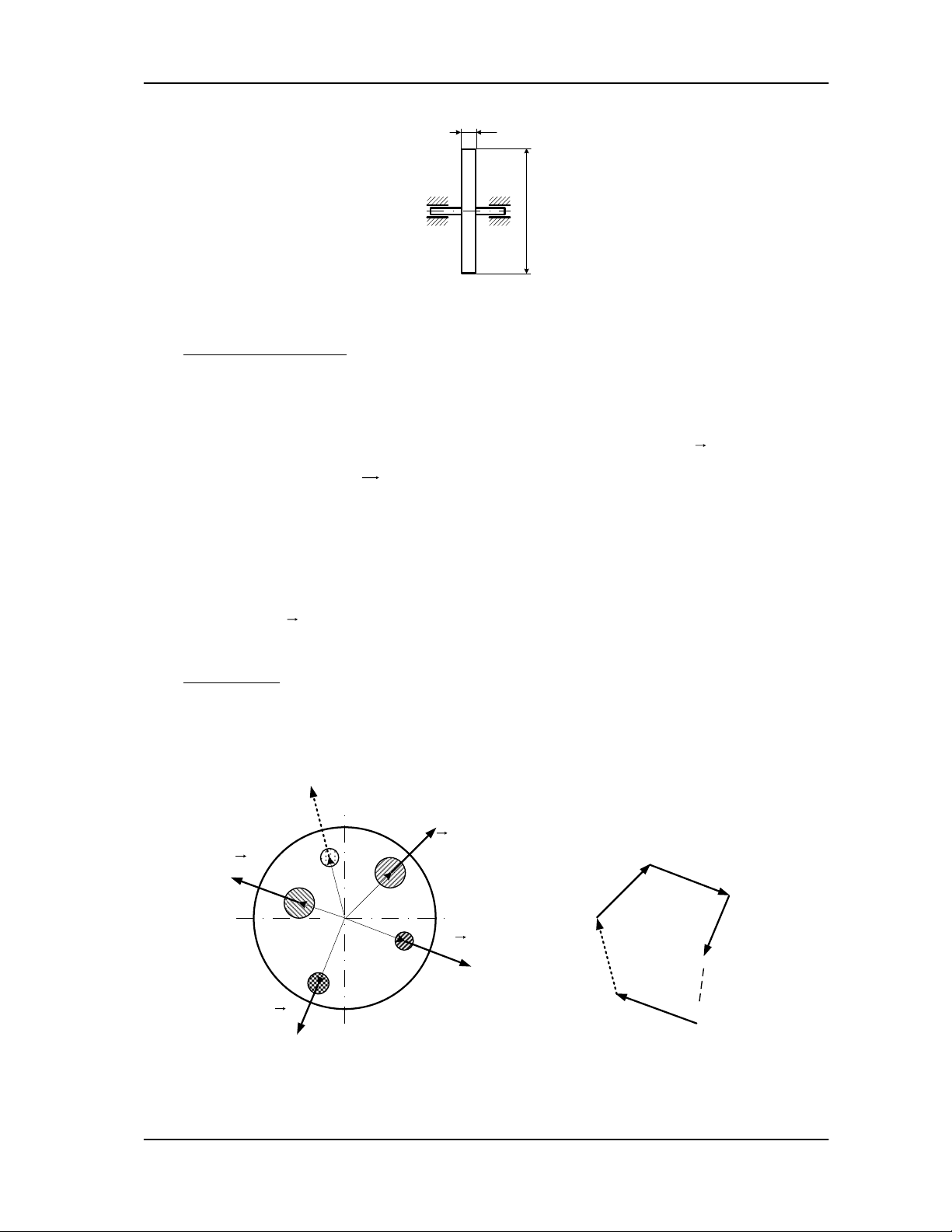
Chöùng minh: Xeùt vaät coù beà daøy nhoû quay quanh taâm O nhö hình 5.2a. Treân vaät coù
caùc khoái löôïng taäp trung )...,,2,1( nimi
=
ôû vò trí ñöôïc xaùc ñònh bôûi baùn kính vector i
r
r
tính töø taâm quay O.
1
m
P
1
qt
2
m
P
2
qt
3
m
P
3
qt
n
m
P
n
qt
m
1
r
r
2
r
r
3
r
r
n
r
r
r
r
rm r
2
ω
O
11
rm
r
22
rm r
33rm r
nn
rm
r
rm
r
a
b
c
p
d
q
a) b)
Hình 5.2
Baøi giaûng NGUYEÂN LYÙ MAÙY Chöông 5: Caân baèng maùy
Bm. Thieát keá maùy TS. Buøi Troïng Hieáu
- 73 -
Khi vaät quay vôùi vaän toác goùc
, caùc khoái löôïng taäp trung seõ gaây ra caùc löïc quaùn tính:
ii
qt rmP i
r
2
ω
= (5.1)
Toång caùc löïc quaùn tính ly taâm baèng:
∑
==
n
iii
qt rmP
1
2r
ω
(5.2)
Neáu vaät maát caân baèng, töùc laø 0
1
2≠
∑
=
n
iii rm r
ω
thì khoái taâm cuûa vaät khoâng truøng vôùi taâm
quay O vì neáu goïi S
r
r
laø baùn kính vector xaùc ñònh vò trí khoái taâm S, ta coù:
0
1
1≠
∑
∑
=
=
=
n
ii
n
iii
S
m
rm
r
r
r (5.3)
Ñeå vaät caân baèng, ta phaûi theâm vaøo moät khoái löôïng m ôû vò trí
r
r
sao cho khi vaät quay
thì löïc quaùn tính do noù gaây ra laø rm
r
2
ω
caân baèng vôùi toång caùc löïc quaùn tính, töùc laø:
0
2
1
2=+
∑
=
rmrm
n
iii
rr
ωω
(5.4)
Hay 0
2211
=
+
+
+
+
rmrmrmrm nn
r
r
L
r
r
(5.5)
Khi phöông trình (5.5) thoûa, khoái taâm chung cuûa löôïng maát caân baèng ∑
=
n
iii rm
1
r vaø ñoái
troïng rmr theâm vaøo seõ veà truøng vôùi taâm quay, töùc laø baùn kính vector xaùc ñònh vò trí
khoái taâm 'S sau khi gaén theâm ñoái troïng laø:
0
321
2211
'=
+++
+
+
+
+
=mmmm
rmrmrmrm
rnn
S
r
r
L
r
r
r (5.6)
⇒ Nguyeân taéc caân baèng ñaõ ñöôïc chöùng minh.
Baøi giaûng NGUYEÂN LYÙ MAÙY Chöông 5: Caân baèng maùy
Bm. Thieát keá maùy TS. Buøi Troïng Hieáu
- 74 -
Phöông trình (5.5) coù theå giaûi baèng phöông phaùp hoïa ñoà vector nhö sau (hình 5.2b):
• Choïn a laøm goác hoïa ñoà vaø ⎥
⎦
⎤
⎢
⎣
⎡
mm
m
l
μ
laø tyû leä xích.
• Töø a veõ ab song song vôùi 1
r
r
bieåu dieãn cho 11rm
r
.
• Töø b veõ bc song song vôùi 2
r
r
bieåu dieãn cho 22rm
r
.
• Töø c veõ cd song song vôùi 3
r
r
bieåu dieãn cho 33rm
r
.
...
• Töø muùt vector bieåu dieãn cho 11 −− nn rm
r
, giaû söû laø
p
, veõ pq song song vôùi
n
r
r bieåu dieãn cho nnrm
r
.
• Vector qa bieåu thò rm
r
caàn tìm. Cho trò soá
r
r
, ta seõ tính ñöôïc giaù trò m.
Nhaän xeùt:
z Moät vaät ñöôïc caân baèng vôùi moät vaän toác goùc naøo ñoù thì cuõng hoaøn toaøn caân baèng vôùi
moïi vaän toác goùc (khoâng phuï thuoäc vaøo
ω
).
z Coù theå thay theá vieäc theâm vaøo khoái löôïng m ôû vò trí
r
r
baèng caùch laáy ñi moät khoái
löôïng m ôû vò trí xuyeân taâm ñoái vôùi
r
r
.
z Coù theå duøng nhieàu ñoái troïng thay cho moät ñoái troïng. Ví duï coù theå thay khoái löôïng m
baèng caùc khoái löôïng i
m′ ôû vò trí i
r
r
′
sao cho rmrm
n
iii
rr =
∑′′
=1
.
z Caàn ít nhaát moät ñoái troïng vaø chæ caàn tieán haønh phaân boá khoái löôïng treân moät maët
phaúng vuoâng goùc vôùi truïc quay.
b). Thí nghieäm caân baèng tónh (khoâng bieát i
m ôû vò trí i
r
r
maø phaûi tìm baèng thí nghieäm)
Moät vaät duø cheá taïo chính xaùc ñeán ñaâu cuõng thöôøng khoâng caân baèng. Trong thöïc teá, ta hoaøn
toaøn khoâng bieát caùc khoái löôïng taäp trung i
m ôû vò trí i
r
r
, neân vieäc xaùc ñònh ñoái troïng rm
r
phaûi ñöôïc tieán haønh baèng thí nghieäm. Nhôø thí nghieäm ta môùi bieát vieäc theâm hoaëc bôùt khoái
löôïng treân vaät quay taïi nhöõng vò trí thích hôïp ñeå cho khoái taâm cuûa vaät veà truøng vôùi truïc quay.
Thí nghieäm naøy coù theå thöïc hieän ôû traïng thaùi tónh neân ñöôïc goïi laø thí nghieäm caân baèng tónh.
Coù nhieàu phöông phaùp caân baèng tónh, ta xeùt hai phöông phaùp sau:
Baøi giaûng NGUYEÂN LYÙ MAÙY Chöông 5: Caân baèng maùy
Bm. Thieát keá maùy TS. Buøi Troïng Hieáu
- 75 -
Phöông phaùp doø tröïc tieáp:
1
2
Hình 5.3
- Duøng hai thanh dao 2 ñaët song song treân maët phaúng naèm ngang ñôõ hai ñaàu truïc quay cuûa vaät
quay 1. Neáu vaät khoâng caân baèng thì noù seõ töï laên treân dao cho ñeán khi troïng taâm naèm ôû vò trí
thaáp nhaát.
- Ñaép saùp (hoaëc ñaát seùt, …) vaøo moät vò trí naøo ñoù treân baùn kính thaúng ñöùng phía treân taâm quay.
Theâm hoaëc bôùt saùp cho ñeán khi vaät quay ñaït traïng thaùi caân baèng phieám ñònh, töùc laø neáu laên
vaät ñeán vò trí naøo thì vaät cuõng ñöùng yeân ôû vò trí ñoù.
- Khoái löôïng vaø vò trí cuûa khoái saùp ñaép vaøo cho ta bieát giaù trò vaø vò trí cuûa ñoái troïng caàn theâm
vaøo ñeå vaät caân baèng. Coù theå ñaép vaøo vò trí cuûa khoái saùp moät khoái vaät lieäu cuøng khoái löôïng
hay khoan ñi moät khoái löôïng nhö vaäy ôû vò trí xuyeân taâm ñoái.
- Öu ñieåm: thieát bò ñôn giaûn, reû tieàn, deã daøng thöïc hieän.
- Nhöôïc ñieåm: + naêng suaát thaáp vì maát nhieàu thôøi gian cho vieäc doø.
+ thieáu chính xaùc vì coù ma saùt laên giöõa truïc quay vaø dao.
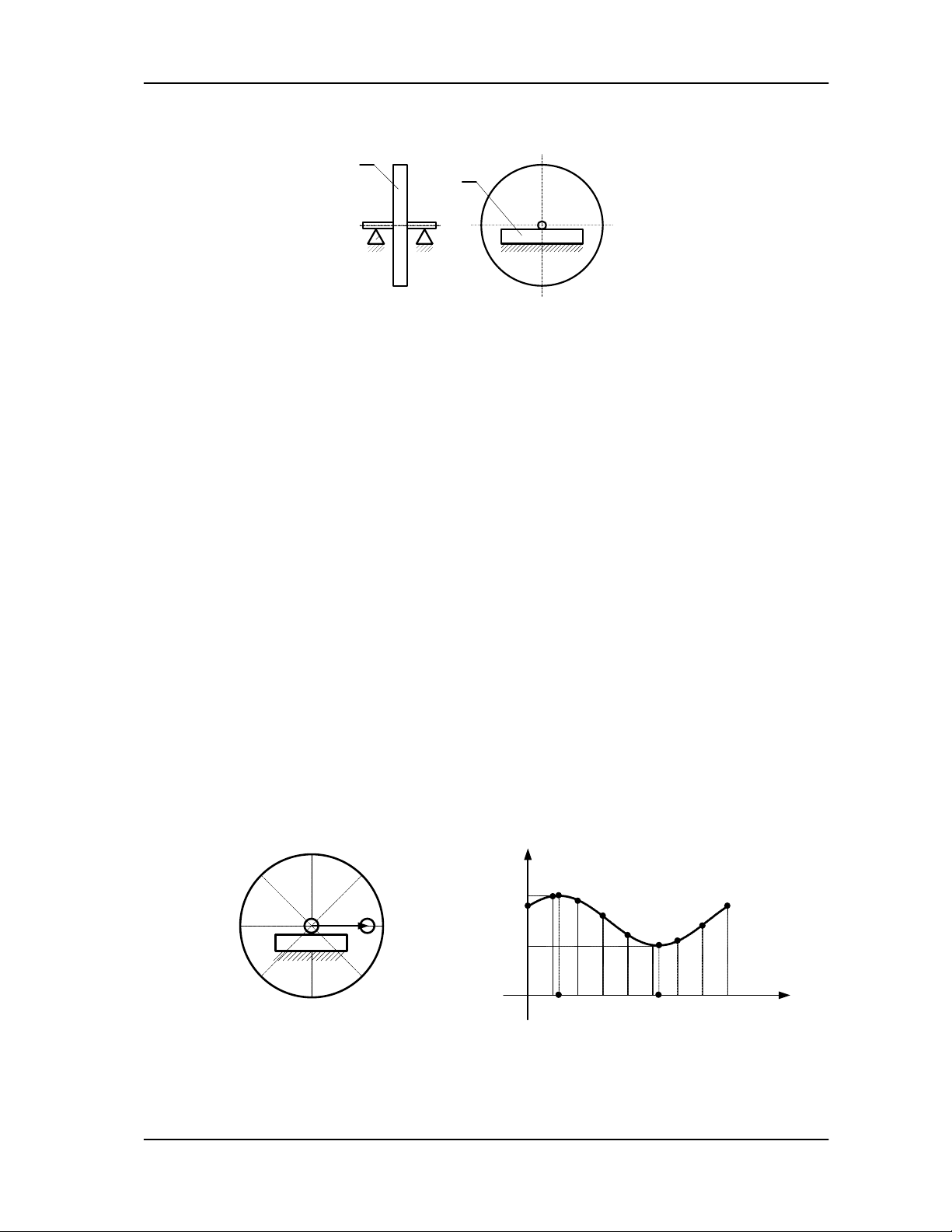
Phöông phaùp hieäu soá moment:
Ñeå traùnh aûnh höôûng cuûa löïc ma saùt, ta tieán haønh thí nghieäm nhö sau:
1
2
3
4
5
6
7
8
R
i
m
123456781
max
m
min
m
m
vò trí
AB
a) b)
Hình 5.4