intTypePromotion=1
zunia.vn Tuyển sinh 2024 dành cho Gen-Z zunia.vn zunia.vn
ADSENSE
 » 
 » 

Bài giảng Quang học: Chương 2 - Huỳnh Trúc Phương

Chia sẻ: _ _ | Ngày: | Loại File: PDF | Số trang:38

Thêm vào BST
Báo xấu
3
lượt xem 2
download
 
  Download Vui lòng tải xuống để xem tài liệu đầy đủ

Bài giảng Quang học: Chương 2 - Nhiễu xạ sóng ánh sáng, được biên soạn gồm các nội dung chính sau: Hiện tượng nhiễu xạ ánh sáng; Nguyên lý Huygens-Fresnel; Nhiễu xạ Fresnel qua lỗ tròn; Nhiễu xạ Fresnel qua đĩa tròn; Nhiễu xạ Fraunhofer qua khe hẹp; Cách tử nhiễu xạ;...Mời các bạn cùng tham khảo!

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài giảng Quang học: Chương 2 - Huỳnh Trúc Phương

  1. BÀI GIẢNG QUANG HỌC HUỲNH TRÚC PHƯƠNG Email: htphuong.oarai@gmail.com
  2. CHƯƠNG 2 NHIỄU XẠ SÓNG ÁNH SÁNG 2.1. Hiện tượng nhiễu xạ AS 2.2. Nguyên lý Huygens-Fresnel 2.3. Nhiễu xạ Fresnel qua lỗ tròn 2.4. Nhiễu xạ Fresnel qua đĩa tròn 2.5. Nhiễu xạ Fraunhofer qua khe hẹp 2.6. Cách tử nhiễu xạ
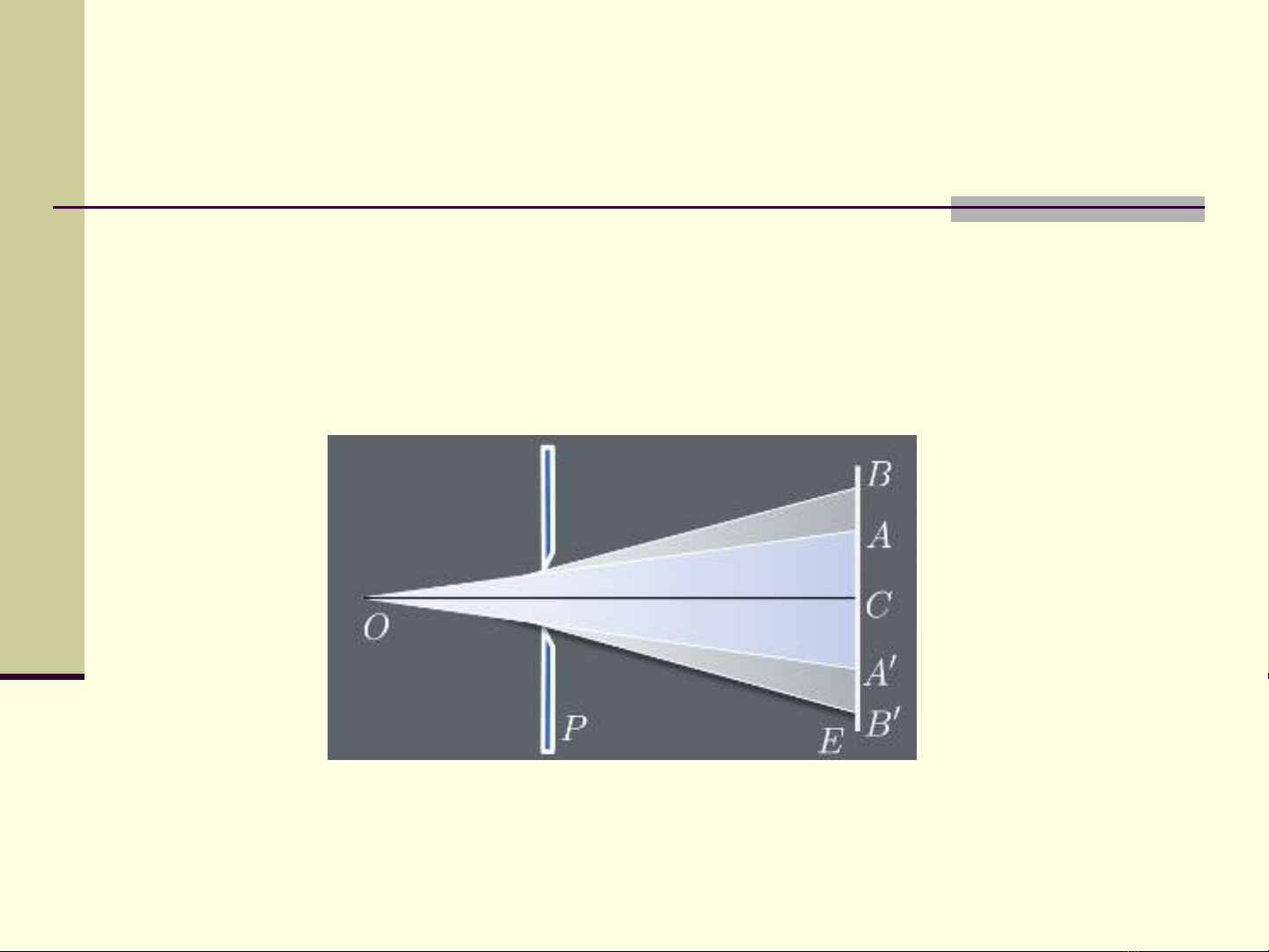
  3. 2.1. GIỚI THIỆU VỀ NỀN NHIỄU XẠ  Khi ánh sáng có bước sóng lớn hơn hay bằng bề rộng của khe thì nó tán xạ qua mọi hướng về phía trước khi nó truyền qua khe. Hiện tượng này được gọi là nhiễu xạ.  Nền nhiễu xạ gồm các vùng sáng – tối xen kẻ nhau, tương tự như nền giao thoa  Chính giữa nền nhiễu xạ sáng nhất gọi là cực đại chính giữa.  Xung quanh cực đại chính giữa có những vùng sáng yếu hơn, được gọi là cực đại thứ cấp.  Những vùng tối được gọi là cực tiễu nhiễu xạ. Nền nhiễu xạ qua khe hẹp
  4. 2.1. GIỚI THIỆU VỀ NỀN NHIỄU XẠ  Hiện tượng nxas là hiện tượng as bị lệch khỏi phương truyền thẳng khi đi gần các vật cản.  Nx gây bởi sóng phẳng gọi là nx Fraunhofer. Trái lại nhiễu xạ gây bởi sóng cầu gọi là nx Fresnel. Chúng ta sẽ tìm hiểu nx qua lỗ tròn và qua khe hẹp
  5. 2.2. NGUYÊN LÝ HUYGENS - FRESNEL 1 – Nội dung: o Bất kì một điểm nào mà as truyền đến đều trở thành nguồn sáng thứ cấp, phát sóng cầu về phía trước nó. o Biên độ và pha của nguồn thứ cấp là biên độ và pha của nguồn thực gây ra tại vị trí nguồn thứ cấp.
  6. 2.2. NGUYÊN LÝ HUYGENS - FRESNEL 2 – Biểu thức sóng: Đặt vấn đề: Giả sử dđ sáng tại nguồn O có dạng E = acost thì dđ sáng tại M có dạng như thế nào? N Giải quyết vấn đề: Chọn mặt kín (S) bao quanh O. dS * Dđ sáng tại A do O truyền đến:   2L1  A r2 E A  a cos  t   r1    o * Dđ sáng tại M do dS truyền đến: O N’ M  2(L1  L2 )  dE M  a M cos  t   (S)    * Dđ sáng tại M do mặt (S) a  2(L1  L2 )  truyền đến: EM   A(, 0 )c os  t   dS rr (S) 1 2   
  7. 2.3. NHIỄU XẠ FRESNEL QUA LỖ TRÒN 1 – Bố trí thí nghiệm: R O b R r b O M
  8. 2.3. NHIỄU XẠ FRESNEL QUA LỖ TRÒN 2 – Phân bố cường độ ảnh nhiễu xạ: Ảnh nx có tính đối xứng tâm M. Tâm M có lúc sáng, lúc tối, tùy theo bán kính lỗ tròn và khoảng cách từ lỗ tròn tới màn quan sát.
  9. 2.3. NHIỄU XẠ FRESNEL QUA LỖ TRÒN  b3 2 3 – Giải thích kết quả bằng pp đới cầu Fresnel:  b2 2 R  b 2 4 2 O 1 b M 5 3 S0
  10. 2.3. NHIỄU XẠ FRESNEL QUA LỖ TRÒN  2 kb r  R  (R  h k )  (b  k )  (b  h k )  h k  2 2 2 2 k 3 – Giải thích kết quả bằng pp đới cầu Fresnel: 2(R  b) 2 Mk Rb  Sk  h k .2R  k. R  Rb rk bk Diện tích của mỗi đới cầu: 2 hk Rb S  O Hk M0 b M Rb k Bán kính của đới cầu thứ k: kRb S0 rk  2Rh k  Rb
  11. 2.3. NHIỄU XẠ FRESNEL QUA LỖ TRÒN 3 – Giải thích kết quả bằng pp đới cầu Fresnel: Biên độ sóng ak do đới thứ k gởi tới M sẽ giảm dần khi chỉ số k tăng, nhưng giảm Dao động sáng tại M do hai đới kề chậm. Vì thế ta coi ak là trung bình cộng nhau gởi tới sẽ ngược pha nhau. Vì thế, của ak-1 và ak+1. biên độ sóng tại M là: 4 2 a  a  a  a  a  ...  a M 1 2 3 4 n O 1 b M 5 3 a1 a n (Dấu “+” khi n lẻ; aM   “-” khi n chẵn) S0 2 2
  12. 2.3. NHIỄU XẠ FRESNEL QUA LỖ TRÒN Kết luận: Biên độ sóng và cường độ sáng tại M: 2 a1 a n  a1 a n  aM    I  aM     2 2 2 2 2 2 a1 o Nếu lỗ tròn quá lớn thì: I  a 2   I0 M 4 2 o Nếu lỗ tròn chứa số lẻ  a1 a n  (M là điểm đới cầu Fresnel thì: Ia 2 M     I0 sáng). 2 2  o Nếu lỗ tròn chứa số 2  a1 a n  (M là điểm chẵn đới cầu Fresnel thì: Ia 2 M     I0 tối).  2 2 
  13. 2.3. NHIỄU XẠ FRESNEL QUA LỖ TRÒN Ví dụ 2.1: Chiếu ánh sáng đơn sắc có bước sóng = 0,5m vào một lỗ tròn có bán kính chưa biết. Nguồn sáng đặt tại điểm cách lỗ tròn 2m, sau lỗ tròn 2m đặt màn quan sát. Hỏi bán kính của lỗ tròn bằng bao nhiêu để tâm của nền nhiễu xạ là tối nhất. Đáp số: r = 1 mm Bài giải Tâm nền nhiễu xạ tối nhất khi lỗ tròn chứa 2 đới cầu Vậy bán kính lỗ tròn phải bằng bán kính đới cầu thứ 2 2Rb r  r2   0,001(m)  1(mm) Rb
  14. 2.3. NHIỄU XẠ FRESNEL QUA LỖ TRÒN Ví dụ 2.2: Một màn đặt cách nguồn sáng ( = 0,5m) khoảng 2m. Chính giữa màn và nguồn sáng là lỗ tròn đường kính 0,2cm. Tính số đới cầu Fresnel mà lỗ tròn chứa được. Tâm của nền nhiễu xạ sáng hay tối? Đáp số: k = 4 Bài giải kRb 2 R  b  r kr   Rb  Rb  Với R + b = 2 m, R = b = 1 m k=4 Tâm của nền nhiễu xạ là điểm tối
  15. 2.3. NHIỄU XẠ FRESNEL QUA LỖ TRÒN Ví dụ 2.3: Chiếu ánh sáng đơn sắc có bước sóng = 0,5m vào một lỗ tròn có bán kính r = 1mm. Khoảng cách từ nguồn sáng đến lỗ tròn R= 1m. Tính khoảng cách từ lỗ tròn đến màn để lỗ tròn chứa 3 đới cầu Fresnel. Bài giải Đáp số: b = 2 m 3Rb r  r3   b  ..... Rb
  16. 2.4. NHIỄU XẠ FRESNEL QUA ĐĨA TRÒN 1 – Thí nghiệm: O b Kết quả: Tâm ảnh nx luôn có một chấm sáng (chấm sáng Fresnel)
  17. 2.4. NHIỄU XẠ FRESNEL QUA ĐĨA TRÒN 2 – Giải thích kết quả: Giả sử đĩa tròn chắn hết m đới cầu Fresnel thì biên độ sáng tại M chỉ do các đới cầu thứ m +1, m +2, … gởi tới. O b M m+1 a1 a m a m1 a  a m1 aM      2 2 2 2 2 2 Cường độ sáng I  a 2   a m 1  Vậy tại M luôn là điểm sáng. M    2 
  18. 2.5. NHIỄU XẠ FRAUNHOFER QUA KHE HẸP B0 θ B1 H M M0 A o Lo 1 L λ/2
  19. 2.5. NHIỄU XẠ FRAUNHOFER QUA KHE HẸP Yêu cầu: Xác định sự phân bố cường độ sáng trên màn quan sát theo góc nhiễu xạ θ và từ đó giải thích hình ảnh nhiễu xạ quan sát được. λ B0 B1  2sinθ 2asinθ n λ
  20. 2.5. NHIỄU XẠ FRAUNHOFER QUA KHE HẸP 2a sin   n  2m sin   m , m  1;2...  a 2a sin  n  2m  1   sin   2m  1 , m  1;2... 2a
ADSENSE

CÓ THỂ BẠN MUỐN DOWNLOAD

THÔNG TIN
TRỢ GIÚP
HỖ TRỢ KHÁCH HÀNG
Theo dõi chúng tôi

Chịu trách nhiệm nội dung:

Nguyễn Công Hà - Giám đốc Công ty TNHH TÀI LIỆU TRỰC TUYẾN VI NA

LIÊN HỆ

Địa chỉ: P402, 54A Nơ Trang Long, Phường 14, Q.Bình Thạnh, TP.HCM

Hotline: 093 303 0098

Email: support@tailieu.vn

Giấy phép Mạng Xã Hội số: 670/GP-BTTTT cấp ngày 30/11/2015 Copyright © 2022-2032 TaiLieu.VN. All rights reserved.

 

Đồng bộ tài khoản
2=>2