Chương 1. TÍCH PHÂN KÉP
1Bài toán tính thể tích vật thể
2Định nghĩa tích phân kép
3Điều kiện khả tích
4Các tính chất cơ bản
5Cách tính tích phân kép trong hệ toạ độ Descartes
6Công thức đổi biến tổng quát
7Đổi biến sang toạ độ cực
8Ứng dụng
BM Toán-Cơ-Tin học (Khoa KHCB) Chương 1. TÍCH PHÂN KÉP 14/9/2020 2 / 35
1. Bài toán tính thể tích vật thể
■Use a double integral to represent the volume of a solid region.■Use properties of double integrals.■Evaluate a double integral as an iterated integral.■Find the average value of a function over a region.Double Integrals and Volume of a Solid RegionYou already know that a definite integral over an intervaluses a limit process to assignmeasures to quantities such as area, volume, arc length, and mass. In this section, youwill use a similar process to define the double integral of a function of two variablesover a region in the plane.Consider a continuous function such that for all in a region in the plane. The goal is to find the volume of the solid region lying between thesurface given bySurface lying above the planeand the plane,as shown in Figure 14.8. You can begin by superimposing a rectan-gular grid over the region,as shown in Figure 14.9. The rectangles lying entirelywithin form an inner partitionwhosenormis defined as the length of thelongest diagonal of the rectangles. Next, choose a point in each rectangle andform the rectangular prism whose height is as shown in Figure 14.10.Because the area of the rectangle is Area of rectangleit follows that the volume of the prism isVolume of prismand you can approximate the volume of the solid region by the Riemann sum of thevolumes of all prisms,Riemann sumas shown in Figure 14.11. This approximation can be improved by tightening the meshof the grid to form smaller and smaller rectangles,as shown in Example 1.
ni1
f
x
i
,y
i
A
i
nithf
x
i
,y
i
A
i
ithithA
i
ithf
x
i
,y
i
,
x
i
,y
i
n,Rxy-xy-zf
x,y
xy-R
x,y
f
x,y
0f992Chapter 14Multiple Integration14.2Double Integrals and VolumeRxySurface:z=f(x,y)z(xi,yi)The rectangles lying within form an innerpartition ofFigure 14.9R.R
x
yzf(xi,yi)Rectangular prism whose base has an area ofand whose height is Figure 14.10f
x
i
,y
i
A
i
xyzVolume approximated by rectangularprismsFigure 14.11xySurface:z=f(x,y)RzFigure 14.8
D
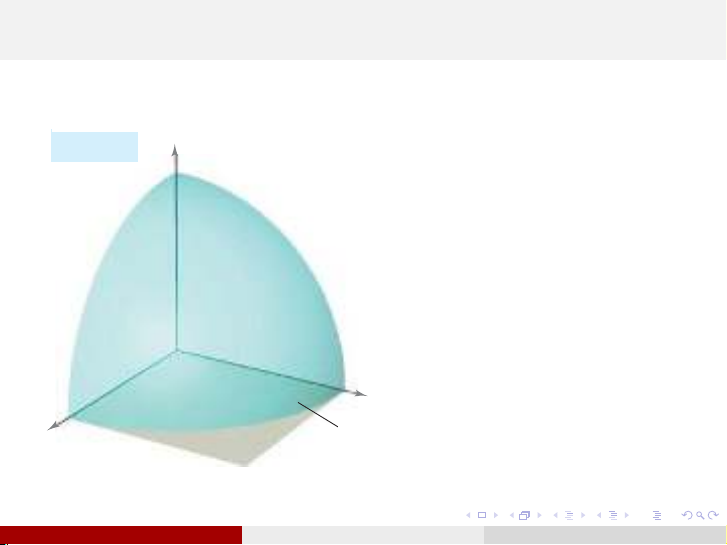
Cho hàm hai biến z=
f(x, y)≥0,∀(x, y)∈D,
trong đó Dlà miền phẳng
trong mặt phẳng Oxy. Tính
thể tích của vật thể nằm
giữa mặt cong z=f(x, y)và
mặt phẳng Oxy.
BM Toán-Cơ-Tin học (Khoa KHCB) Chương 1. TÍCH PHÂN KÉP 14/9/2020 3 / 35
■Use a double integral to represent the volume of a solid region.■Use properties of double integrals.■Evaluate a double integral as an iterated integral.■Find the average value of a function over a region.Double Integrals and Volume of a Solid RegionYou already know that a definite integral over an intervaluses a limit process to assignmeasures to quantities such as area, volume, arc length, and mass. In this section, youwill use a similar process to define the double integral of a function of two variablesover a region in the plane.Consider a continuous function such that for all in a region in the plane. The goal is to find the volume of the solid region lying between thesurface given bySurface lying above the planeand the plane,as shown in Figure 14.8. You can begin by superimposing a rectan-gular grid over the region,as shown in Figure 14.9. The rectangles lying entirelywithin form an inner partitionwhosenormis defined as the length of thelongest diagonal of the rectangles. Next, choose a point in each rectangle andform the rectangular prism whose height is as shown in Figure 14.10.Because the area of the rectangle is Area of rectangleit follows that the volume of the prism isVolume of prismand you can approximate the volume of the solid region by the Riemann sum of thevolumes of all prisms,Riemann sumas shown in Figure 14.11. This approximation can be improved by tightening the meshof the grid to form smaller and smaller rectangles,as shown in Example 1.
ni1
f
x
i
,y
i
A
i
nithf
x
i
,y
i
A
i
ithithA
i
ithf
x
i
,y
i
,
x
i
,y
i
n,Rxy-xy-zf
x,y
xy-R
x,y
f
x,y
0f992Chapter 14Multiple Integration14.2Double Integrals and VolumeRxySurface:z=f(x,y)z(xi,yi)The rectangles lying within form an innerpartition ofFigure 14.9R.R
x
yzf(xi,yi)Rectangular prism whose base has an area ofand whose height is Figure 14.10f
x
i
,y
i
A
i
xyzVolume approximated by rectangularprismsFigure 14.11xySurface:z=f(x,y)RzFigure 14.8
D
■Use a double integral to represent the volume of a solid region.■Use properties of double integrals.■Evaluate a double integral as an iterated integral.■Find the average value of a function over a region.Double Integrals and Volume of a Solid RegionYou already know that a definite integral over an intervaluses a limit process to assignmeasures to quantities such as area, volume, arc length, and mass. In this section, youwill use a similar process to define the double integralof a function of two variablesover a region in the plane.Consider a continuous function such that for all in a region in the plane. The goal is to find the volume of the solid region lying between thesurface given bySurface lying above the planeand the plane,as shown in Figure 14.8. You can begin by superimposing a rectan-gular grid over the region,as shown in Figure 14.9. The rectangles lying entirelywithin form an inner partitionwhosenormis defined as the length of thelongest diagonal of the rectangles. Next, choose a point in each rectangle andform the rectangular prism whose height is as shown in Figure 14.10.Because the area of the rectangle is Area of rectangleit follows that the volume of the prism isVolume of prismand you can approximate the volume of the solid region by the Riemann sum of thevolumes of all prisms,Riemann sumas shown in Figure 14.11. This approximation can be improved by tightening the meshof the grid to form smaller and smaller rectangles,as shown in Example 1.
ni1
f
x
i
,y
i
A
i
nithf
x
i
,y
i
A
i
ithithA
i
ithf
x
i
,y
i
,
x
i
,y
i
n,Rxy-xy-zf
x,y
xy-R
x,y
f
x,y
0f992Chapter 14Multiple Integration14.2Double Integrals and VolumeRxySurface:z=f(x,y)z(xi,yi)The rectangles lying within form an innerpartition ofFigure 14.9R.Rxyzf(xi,yi)Rectangular prism whose base has an area ofand whose height is Figure 14.10f
x
i
,y
i
A
i
xyzVolume approximated by rectangularprismsFigure 14.11xySurface:z=f(x,y)RzFigure 14.8
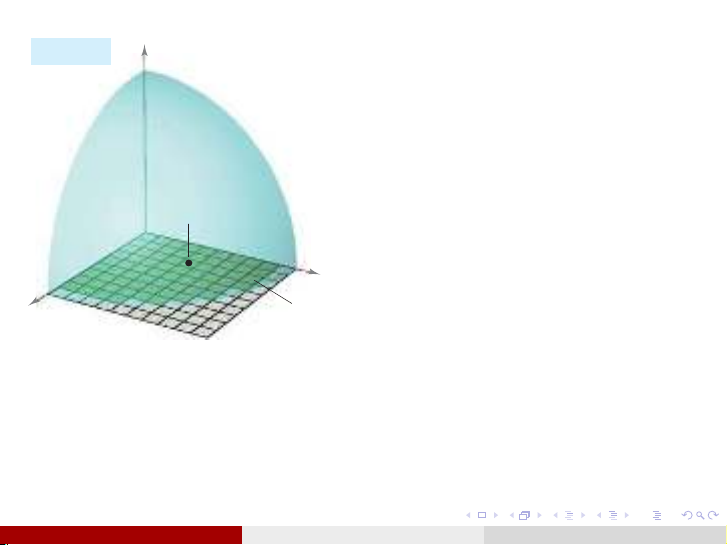
Chia nhỏ miền Dthành n
miền con hình chữ nhật Di
với diện tích ∆si.
Trong miền Dilấy một điểm
(xi, yi).
BM Toán-Cơ-Tin học (Khoa KHCB) Chương 1. TÍCH PHÂN KÉP 14/9/2020 4 / 35
■Use a double integral to represent the volume of a solid region.■Use properties of double integrals.■Evaluate a double integral as an iterated integral.■Find the average value of a function over a region.Double Integrals and Volume of a Solid RegionYou already know that a definite integral over an intervaluses a limit process to assignmeasures to quantities such as area, volume, arc length, and mass. In this section, youwill use a similar process to define the double integral of a function of two variablesover a region in the plane.Consider a continuous function such that for all in a region in the plane. The goal is to find the volume of the solid region lying between thesurface given bySurface lying above the planeand the plane,as shown in Figure 14.8. You can begin by superimposing a rectan-gular grid over the region,as shown in Figure 14.9. The rectangles lying entirelywithin form an inner partitionwhosenormis defined as the length of thelongest diagonal of the rectangles. Next, choose a point in each rectangle andform the rectangular prism whose height is as shown in Figure 14.10.Because the area of the rectangle is Area of rectangleit follows that the volume of the prism isVolume of prismand you can approximate the volume of the solid region by the Riemann sum of thevolumes of all prisms,Riemann sumas shown in Figure 14.11. This approximation can be improved by tightening the meshof the grid to form smaller and smaller rectangles,as shown in Example 1.
ni1
f
x
i
,y
i
A
i
nithf
x
i
,y
i
A
i
ithithA
i
ithf
x
i
,y
i
,
x
i
,y
i
n,Rxy-xy-zf
x,y
xy-R
x,y
f
x,y
0f992Chapter 14Multiple Integration14.2Double Integrals and VolumeRxySurface:z=f(x,y)z(xi,yi)The rectangles lying within form an innerpartition ofFigure 14.9R.R
x
yzf(xi,yi)Rectangular prism whose base has an area ofand whose height is Figure 14.10f
x
i
,y
i
A
i
xyzVolume approximated by rectangularprismsFigure 14.11xySurface:z=f(x,y)RzFigure 14.8
D
■Use a double integral to represent the volume of a solid region.■Use properties of double integrals.■Evaluate a double integral as an iterated integral.■Find the average value of a function over a region.Double Integrals and Volume of a Solid RegionYou already know that a definite integral over an intervaluses a limit process to assignmeasures to quantities such as area, volume, arc length, and mass. In this section, youwill use a similar process to define the double integral of a function of two variablesover a region in the plane.Consider a continuous function such that for all in a region in the plane. The goal is to find the volume of the solid region lying between thesurface given bySurface lying above the planeand the plane,as shown in Figure 14.8. You can begin by superimposing a rectan-gular grid over the region,as shown in Figure 14.9. The rectangles lying entirelywithin form an inner partitionwhosenormis defined as the length of thelongest diagonal of the rectangles. Next, choose a point in each rectangle andform the rectangular prism whose height is as shown in Figure 14.10.Because the area of the rectangle is Area of rectangleit follows that the volume of the prism isVolume of prismand you can approximate the volume of the solid region by the Riemann sum of thevolumes of all prisms,Riemann sumas shown in Figure 14.11. This approximation can be improved by tightening the meshof the grid to form smaller and smaller rectangles,as shown in Example 1.
ni1
f
x
i
,y
i
A
i
nithf
x
i
,y
i
A
i
ithithA
i
ithf
x
i
,y
i
,
x
i
,y
i
n,Rxy-xy-zf
x,y
xy-R
x,y
f
x,y
0f992Chapter 14Multiple Integration14.2Double Integrals and VolumeRxySurface:z=f(x,y)z(xi,yi)The rectangles lying within form an innerpartition ofFigure 14.9R.R
x
yzf(xi,yi)Rectangular prism whose base has an area ofand whose height is Figure 14.10f
x
i
,y
i
A
i
xyzVolume approximated by rectangularprismsFigure 14.11xySurface:z=f(x,y)RzFigure 14.8
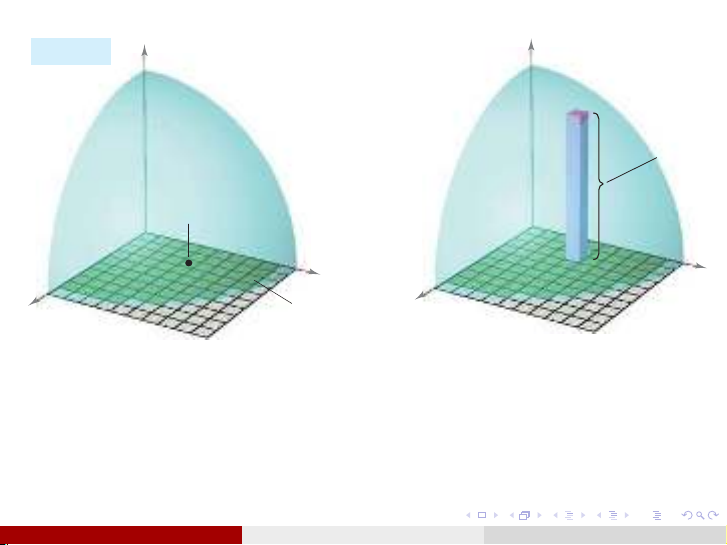
Chia nhỏ miền Dthành n
miền con hình chữ nhật Di
với diện tích ∆si.
Trong miền Dilấy một điểm
(xi, yi).
BM Toán-Cơ-Tin học (Khoa KHCB) Chương 1. TÍCH PHÂN KÉP 14/9/2020 4 / 35
