Chương 3. TÍCH PHÂN ĐƯỜNG
1TÍCH PHÂN ĐƯỜNG LOẠI 1
Định nghĩa tích phân đường loại 1
Tính chất
Công thức tính tích phân đường loại 1
2TÍCH PHÂN ĐƯỜNG LOẠI 2
Định nghĩa tích phân đường loại 2
Tính chất
Công thức tính tích phân đường loại 2
Tích phân không phụ thuộc đường đi
BM Toán-Cơ-Tin học (Khoa KHCB) Chương 3. TÍCH PHÂN ĐƯỜNG 16/10/2020 2 / 33

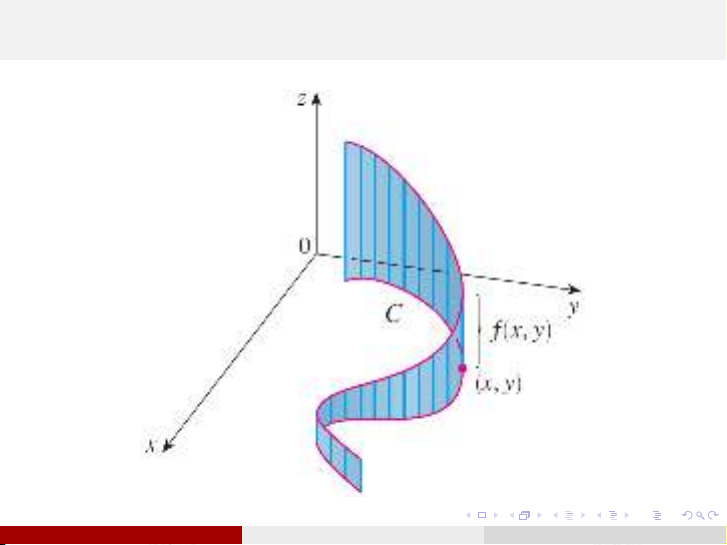
Cho hàm hai biến fxác định trên cung ˆ
AB trong mặt phẳng
Oxy.
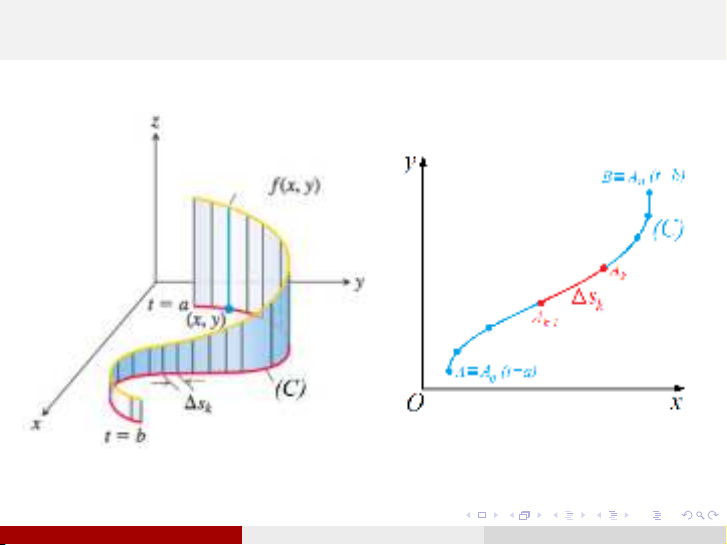
Chia cung ˆ
AB thành ncung cong con bởi các điểm chia
A≡A0, A1, . . . , Ak−1, Ak, . . . , An≡B.
Gọi ∆sklà độ dài cung cong con ˚
Ak−1Ak.
Trên ˚
Ak−1Aklấy điểm Mk(xk;yk)tuỳ ý.
Lập tổng tích phân Sn=
n
X
k=1
f(xk;yk)∆sk.
Cho n→+∞sao cho max ∆sk→0. Nếu Sncó giới hạn
tồn tại hữu hạn, không phụ thuộc cách chia ˆ
AB và cách
lấy các điểm Mkthì giới hạn đó được gọi là tích phân
đường loại 1 của f(x;y)dọc theo ˆ
AB.
BM Toán-Cơ-Tin học (Khoa KHCB) Chương 3. TÍCH PHÂN ĐƯỜNG 16/10/2020 5 / 33