TRÍ TUỆNHÂN TẠO
ThS. Nguyễn ThịThúy Loan
6/8/2010 Nguyễn ThịThúy Loan 2
Cách đánh giá
Thực hành: 30%
Bài tập: 20%
Lý thuyết: 50%
6/8/2010 Nguyễn ThịThúy Loan 3
Tài liệu tham khảo
[1]. Bài giảng của Nguyễn ThịThúy Loan
[2]. Trí tuệnhân tạo, Đỗ Trung Tuấn, NXB Giáo
dục, 1998.
[3]. Bạch Hưng Khang – Hoàng Kiếm, Trí tuệnhân
tạo, NXB KHKT - 1989.
[4]. Lập trình C cho TTNT, 3C soft (dịch), NXB Đại
học và Trung học chuyên nghiệp Hà nội –
1990.
[5]. Trang web
http://ocw.mit.edu/OcwWeb/Electrical-
Engineering-and-Computer-Science/index.htm
6/8/2010 Nguyễn ThịThúy Loan 4
NỘI DUNG
Các thuật giải tô màu đồ thị.
Các thuật giải tìm kiếm trên đồ thị.
Biểu diễn và xửlý tri thức.
Phân lớp.
ThS. Nguyễn ThịThúy Loan
Chương I
CÁC THUẬT GIẢI TÔ
MÀU ĐỒTHỊ
6/8/2010 Nguyễn ThịThúy Loan 6
6
Bài toán
Cho một đồ thịgồm n đỉnh. Quan hệgiữa
đỉnh i và đỉnh j, kí hiệu Qhij, là 1 nếu đỉnh i
có nối với đỉnh j và 0 nếu ngược lại.
Bài toán đặt ra là làm thếnào để tô màu đồ
thịsao cho không tồn tại hai đỉnh có quan hệ
với nhau được tô chung một màu với sốmàu
cần tô là ít nhất?
6
6/8/2010 Nguyễn ThịThúy Loan 7
7
Tô 3 màu Ít nhất chưa?
7
a
bc
d
p
h
e
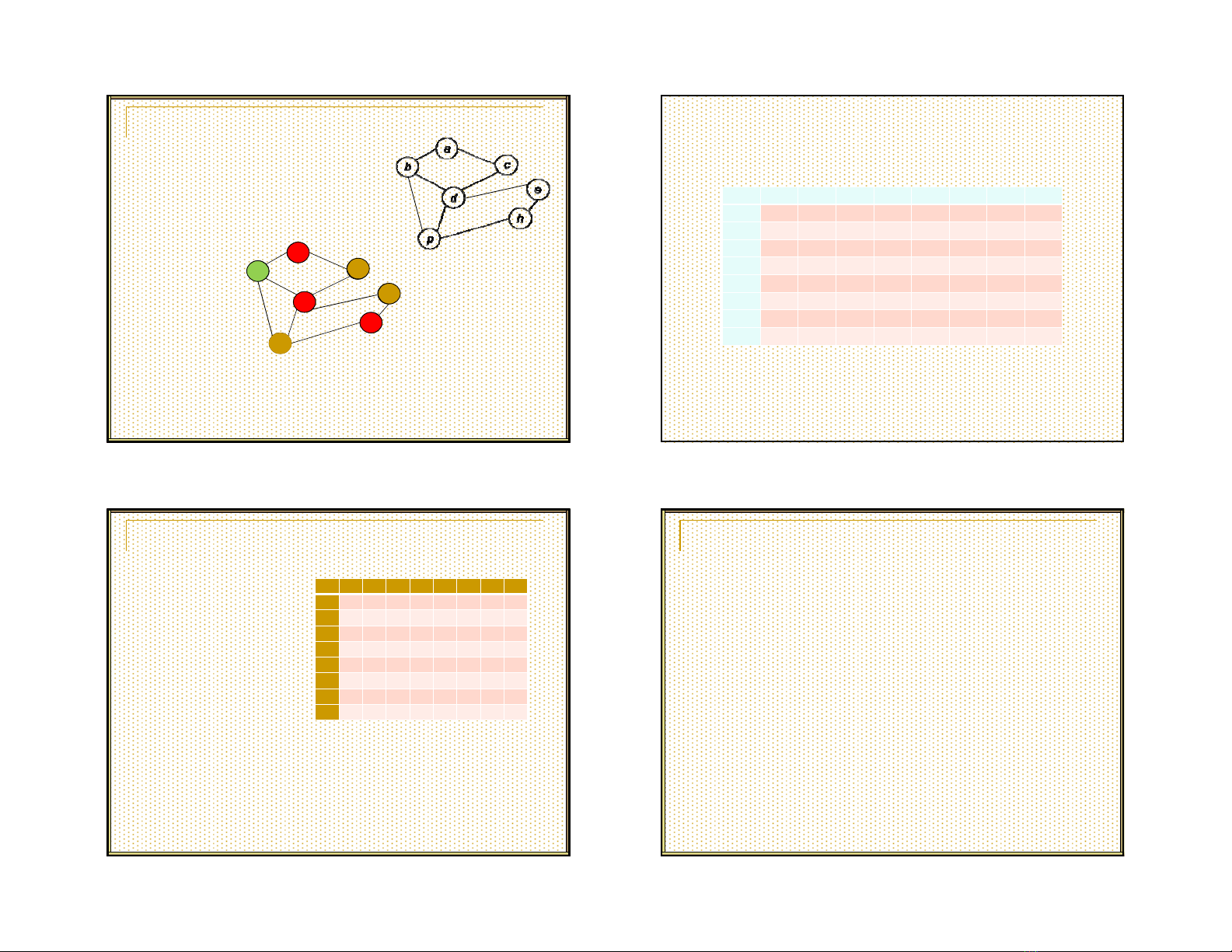
Ví dụ
6/8/2010 Nguyễn ThịThúy Loan 8
8
Thuật giải tô màu “Tối ưu”
Bước 1: [Tô màu] Tô màu i (i bắt đầu xét từ 1) cho đỉnh
có bậc lớn nhất.
Bước 2: [Hạbậc & cấm tô]
2.1. Bậc của đỉnh được tô màu i thì bậc:=0.
2.2. Bậc của đỉnh có quan hệvới đỉnh được tô màu i thì
bậc:= bâc – 1.
2.3. Cấm tô màu i cho đỉnh có quan hệvới đỉnh được tô
màu i.
Bước 3: Lặp lại bước 1 cho đến khi tất cảcác đỉnh đều
được tô màu.
8
6/8/2010 Nguyễn ThịThúy Loan 9
9
Minh họa
9
d
b
p
c
e
h
aa
bc
d
p
h
e
10
Một công ty có 8 đài phát thanh A, B, C, D, E, F, G, H có
khoảng cách (km) được cho trong ma trận sau:
Do yêu cầu kỹthuật nên các đài có khoảng cách 100km
không được dùng chung một trạm phát sóng. Hãy lắp đặt các
trạm phát sóng sao cho sốtrạm cần lắp là nhỏnhất. 10
A B C D E F G H
A0100 50 30 200 150 40 120
B030 80 120 50 200 150
C0120 100 30 80 50
D050 120 150 30
E0200 120 120
F0180 150
G050
H0
Ví dụ
6/8/2010 Nguyễn ThịThúy Loan 11
11
1. Xác định đồ thị
a) Đỉnh:
b) Cung:
11
A B C D E F G H
A 0 100 50 30 200 150 40 120
B 0 30 80 120 50 200 150
C 0 120 100 30 80 50
D 0 50 120 150 30
E 0 200 120 120
F 0 180 150
G 0 50
H 0
Giải quyết
6/8/2010 Nguyễn ThịThúy Loan 12
12
2. Áp dụng thuật giải
để tô màu
12
Kết quả:
Giải quyết
6/8/2010 Nguyễn ThịThúy Loan 13
13
Thuật giải tham lam (Greedy)
Bước 1:
i := 0
Bước 2:
i := i+1
Tô màu i cho tất cảcác đỉnh có thể tô được.
Bước 3:
Lặp lại bước 2 cho đến khi tất cảcác đỉnh
đều được tô màu.
13 14
Ví dụ
Cho ma trận bên
14
AC AD AF BC BD BE CE DE DF EF
AC 0 1 1 1 0 0 1 0 0 0
AD 1 0 1 0 1 0 0 1 1 0
AF 1 1 0 0 0 0 0 0 1 1
BC 1 0 0 0 1 1 1 0 0 0
BD 0 1 0 1 0 1 0 1 1 0
BE 0 0 0 1 1 0 1 1 0 1
CE 1 0 0 1 0 1 0 1 0 1
DE 0 1 0 0 1 1 1 0 1 1
DF 0 1 1 0 1 0 0 1 0 1
EF 0 0 1 0 0 1 1 1 1 0
AC AD AF BC BD BE CE DE DF EF
i=1 1
i=1 11
i=1 11 1
AD AF BC BE CE DE DF
i=2 2
i=2 22
AF BE CE DE DF
i=3 3
i=3 3 3
CE DE DF
i=4 4
i=4 44
DE
i=5 5
6/8/2010 Nguyễn ThịThúy Loan 15
15
Thuật giải sắp thứtự+
tham lam
Bước 1:
Sắp xếp các đỉnh theo chiều giảm dần của
bậc.
i := 0
Bước 2:
i := i+1
Tô màu i cho tất cảcác đỉnh có thể tô được (xét
từtrái sang).
Bước 3:
Lặp lại bước 2 cho đến khi tất cảcác đỉnh đều
được tô màu.
15 16
Ví dụ
Cho ma trận
bên
16
AC AD AF BC BD BE CE DE DF EF Bậc
AC 0 1 1 1 0 0 1 0 0 0 4
AD 1 0 1 0 1 0 0 1 1 0 5
AF 1 1 0 0 0 0 0 0 1 1 4
BC 1 0 0 0 1 1 1 0 0 0 4
BD 0 1 0 1 0 1 0 1 1 0 5
BE 0 0 0 1 1 0 1 1 0 1 5
CE 1 0 0 1 0 1 0 1 0 1 5
DE 0 1 0 0 1 1 1 0 1 1 6
DF 0 1 1 0 1 0 0 1 0 1 5
EF 0 0 1 0 0 1 1 1 1 0 5
DE AD BD BE CE DF EF AC AF BC
i=1 1
i=1 11
AD BD BE CE DF EF AF BC
i=2 2
i=2 22
BD CE DF EF AF BC
i=3 3
i=3 3 3
i=3 3 3 3
DF EF BC
i=4 4
i=4 44
EF
i=5 5
6/8/2010 Nguyễn ThịThúy Loan 17
17
Ví dụ
Một cuộc hội thảo có 9 chủ đề a, b, c, d, e, f, g,
h, i biết rằng các chủ đề sau không được phép
diễn ra trong cùng một buổi: ac, bde, adg, cdf,
dfg, egh, ghi.
Hãy sắp xếp các chủ đề vào các buổi sao cho số
buổi diễn ra là ít nhất.
17
6/8/2010 Nguyễn ThịThúy Loan 18
18
Ví dụ
Học kì II năm 2009 -2010, Phòng ĐT muốn tổ
chức thi các môn A,B,C,D,E,F,G,H,I biết rằng
các môn sau không được thi chung một buổi.
ABC, AE, BCD, BHI, EFG, EI, GHI.
Hãy sắp xếp lịch thi sao cho sốbuổi thi cần sắp
là ít nhất.
18
6/8/2010 Nguyễn ThịThúy Loan 19
19
Ví dụ
Cho ngã năm giao thông như sau trong đó BE là
đường 1 chiều:
19
B
A
E
D
C
Yêu cầu:
1. Xác định đồ thị.
2. Tô màu đồ thị.
Sao cho tại mỗi thời điểm,
các tuyến lưu thông
không giao nhau. ThS. Nguyễn ThịThúy Loan
Chương II
CÁC PHƯƠNG PHÁP
TÌM KIẾM LỜI GIẢI
Ref: http://www.cs.cmu.edu/~awm/tutorials
Phần 1