Bài tập trắc nghiệm môn Toán lớp 9
A. PHẦN ĐẠI SỐ
I/ ĐIỀU KIỆN XÁC ĐỊNH CỦA BIỂU THỨC – CĂN THỨC:
Hãy chọn câu trả lời đúng trong các câu sau:
1. Căn bậc hai số học của số a không âm là:
A. số có bình phương bằng a B.
a
C.
a
D.
a
2. Căn bậc hai số học của
2
( 3)
là :
A.
3
B.
3
C.
81
D.
81
3. Cho hàm số
( ) 1y f x x
. Biến số x có thể có giá trị nào sau đây:
A.
B.
1x
C.
1x
D.
4. Cho hàm số:
2
( ) 1
y f x x
. Biến số x có thể có giá trị nào sau đây:
A.
B.
C.
0x
D.
1x
5. Căn bậc hai số học của
2 2
5 3
là:
A. 16 B. 4 C.
4
D.
4
.
6. Căn bậc ba của
125
là:
A. 5 B.
5
C.
5
D.
25
7. Kết quả của phép tính
25 144
là:
A. 17 B. 169
C. 13 D.
13
8. Biểu thức
xác định khi và chỉ khi:
A.
3x
và
1x
B.
0x
và
1x
C.
0x
và
1x
C.
0x
và
1x
9. Tính
2 2
5 ( 5)
có kết quả là:
A.
0
B.
10
C.
50
D.
10
10. Tính:
2
1 2 2
có kết quả là:
A.
1 2 2
B.
2 2 1
C. 1 D.
1
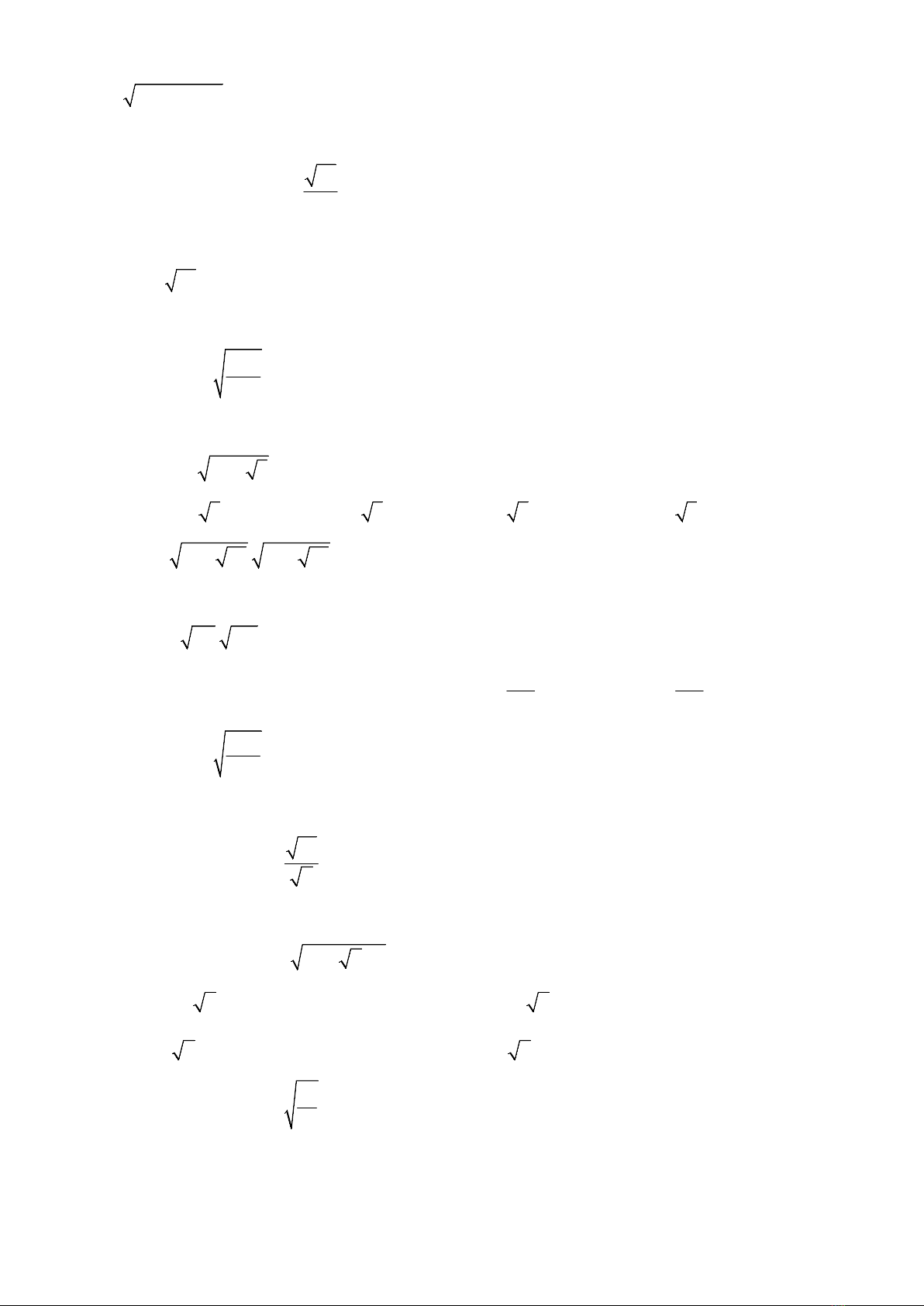
11.
22 1x x
xác định khi và chỉ khi:
A.
x R
B.
1x
C.
x
D.
1x
12. Rút gọn biểu thức:
2
x
x
với x> 0 có kết quả là:
A.
x
B.
1
C. 1 D. x
13. Nếu
2
a a
thì :
A.
0a
B.
1a
C.
0a
D.
0a
14. Biểu thức
2
1
x
x
xác định khi và chỉ khi:
A.
1x
B.
C.
x R
D.
0x
15. Rút gọn
4 2 3
ta được kết quả:
A.
2 3
B.
1 3
C.
3 1
D.
3 2
16. Tính
17 33. 17 33
có kết quả là:
A.
16
B.
256
C. 256 D. 16
17. Tính
0,1. 0,4
kết quả là:
A.
0,2
B.
0,2
C.
4
100
D.
4
100
18. Biểu thức
2
1x
xác định khi :
A. x >1 B. x1 C. x < 1 D. x
0
19. Rút gọn biểu thức
3
a
a
với a> 0, kết quả là:
A.
2
a
B.
a
C.
a
D.
a
20. Rút gọn biểu thức:
2 1x x
với x
0, kết quả là:
A.
1x
B.
1x
C.
D.
21. Rút gọn biểu thức
3
a
a
với a< 0, ta được kết quả là:
A. aB. a2C.
|a| D.
a
22. Cho a, b R. Trong các khẳng định sau khẳng định nào đúng:
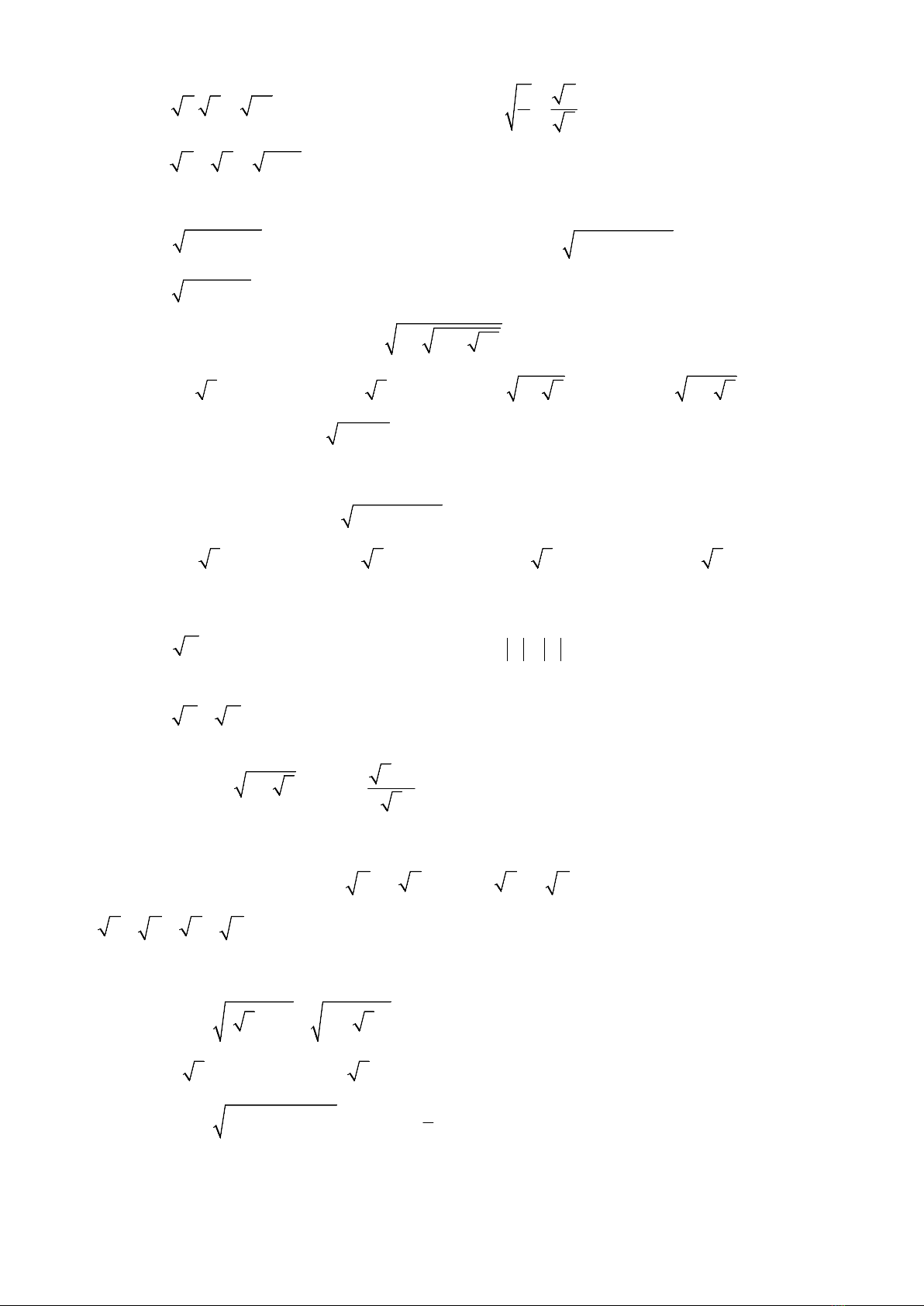
A.
.a b ab
B.
a a
bb
(với a0; b> 0)
C.
a b a b
(với a, b 0) D. A, B, C đều đúng.
23. Trong các biểu thức dưới đây, biểu thức nào được xác định với
x R
.
A.
22 1x x
B.
1 2x x
C.
21x x
D. Cả A, B và C
24. Sau khi rút gọn, biểu thức
3 13 48A
bằng số nào sau đây:
A.
B.
2 3
C.
1 3
D.
2 3
25. Giá trị lớn nhất của
2
16y x
bằng số nào sau đây:
A. 0 B. 4 C. 16 D. Một kết quả khác
26. Giá trị nhỏ nhất của
2
2 2 4 5y x x
bằng số nào sau đây:
A.
2 3
B.
C.
3 3
D.
2 3
27. Câu nào sau đây đúng:
A.
2
0B
A B A B
C.
A B A B
B.
0
00
A
A B B
D. Chỉ có A đúng
28. So sánh
2 5M
và
5 1
3
N
, ta được:
A. M=NB. M<NC. M>ND. MN
29. Cho ba biểu thức :
P x y y x
;
Q x x y y
;
R x y
. Biểu thức nào bằng
x y x y
( với x, y đều dương).
A. PB. QC. RD. Pvà R
30. Biểu thức
2 2
3 1 1 3
bằng:
A.
2 3
B.
3 3
C. 2 D. -2
31. Biểu thức
2
4 1 6 9x x
khi
1
3
x
bằng.
A.
2 3x x
B.
2 1 3x
C.
2 1 3x
D.
2 1 3x
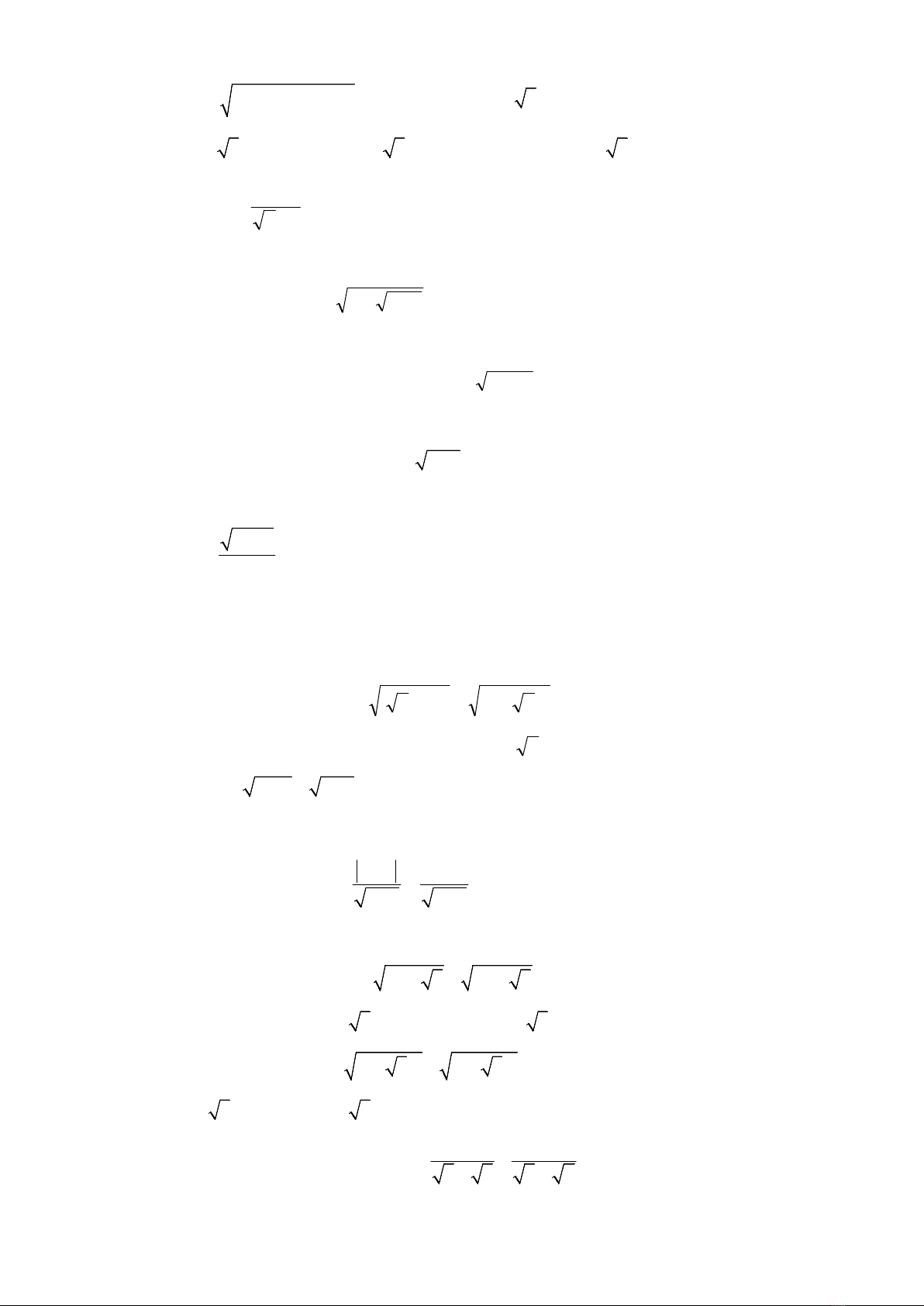
32. Giá trị của
2 2
9 4 4a b b
khi a= 2 và
3b
, bằng số nào sau đây:
A.
6 2 3
B.
6 2 3
C.
3 2 3
D. Một số khác.
33. Biểu thức
1
1
x
P
xác định với mọi giá trị của x thoả mãn:
A.
1x
B.
0x
C.
0x
và
1x
D.
1x
34. Nếu thoả mãn điều kiện
214 x
thì x nhận giá trị bằng:
A. 1 B. - 1 C. 17 D. 2
35. Điều kiện xác định của biểu thức
10)( xxP
là:
A.
10x
B.
C.
10x
D.
10x
36. Điều kiện xác định của biểu thức
là :
A.
x
B.
C.
1x
D.
1x
37. Biểu thức
2
2
1
1
x
x
được xác định khi xthuộc tập hợp nào dưới đây:
A.
/ 1x x
B.
/ 1x x
C.
/ 1;1x x
D. Chỉ có A, C đúng
38. Kết quả của biểu thức:
22 7257 M
là:
A. 3 B. 7 C.
72
D. 10
39. Phương trình
4 1 2x x
có tập nghiệm S là:
A.
1; 4S
B.
1S
C.
D.
4S
40. Nghiệm của phương trình
22
1 1
xx
x x
thoả điều kiện nào sau đây:
A.
1x
B.
2x
C.
2x
D. Một điều kiện khác
41. Giá trị nào của biểu thức
7 4 3 7 4 3S
là:
A. 4 B.
2 3
C.
2 3
D.
4
42. Giá trị của biểu thức
2 3
3
(1 3) (1 3)M
là
A.
2 2 3
B.
2 3 2
C. 2 D. 0
43. Trục căn thức ở mẫu của biểu thức
1 1
3 5 5 7
ta có kết quả:
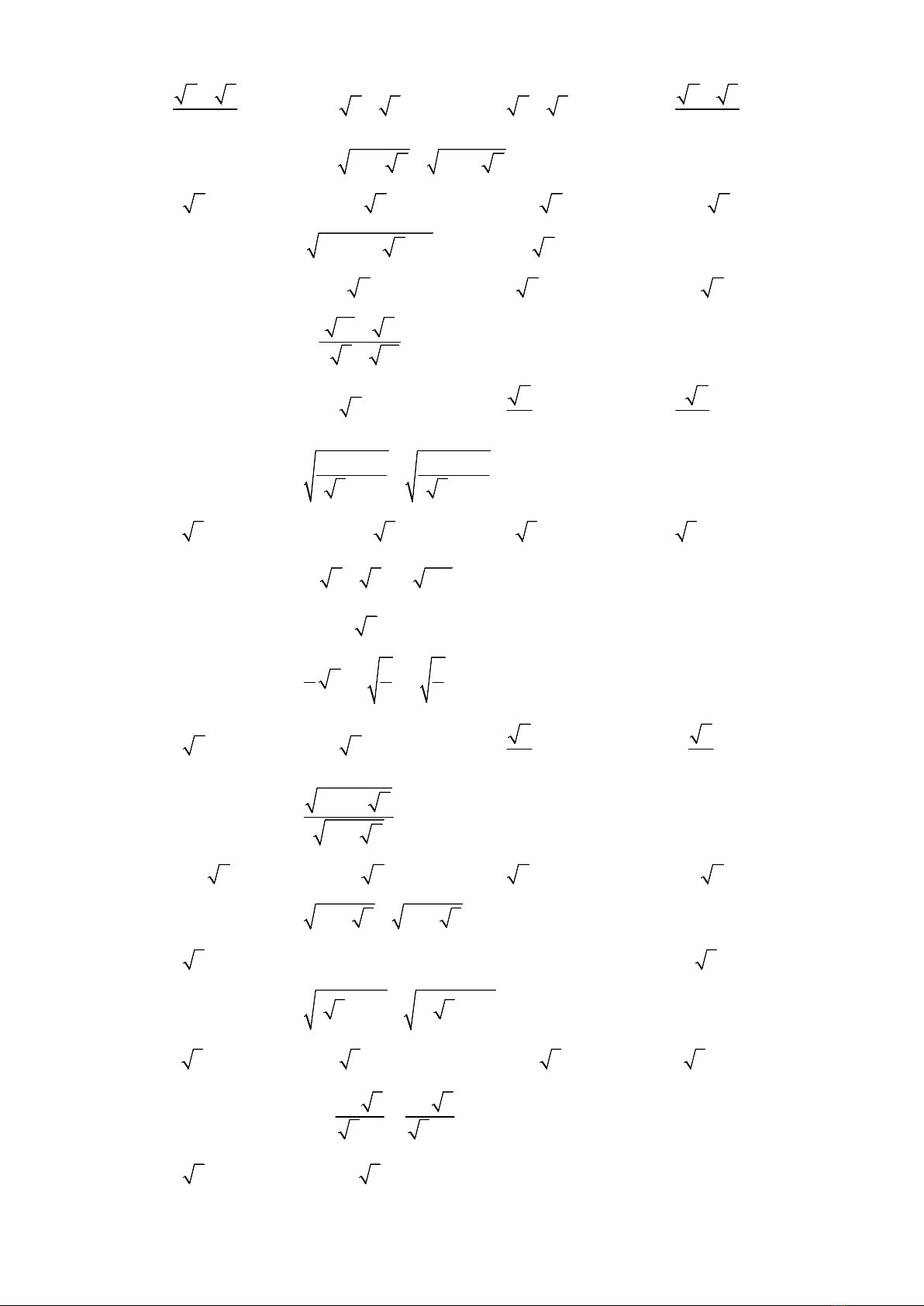
A.
7 3
2
B.
7 3
C.
7 3
D.
7 3
2
44. Giá trị của biểu thức
6 4 2 19 6 2A
là:
A.
7 2 5
B.
5 2
C.
5 3 2
D.
1 2 2
45. Giá trị của biểu thức
2
2 4 2 4a a
với
2 2a
là :
A. 8 B.
3 2
C.
2 2
D.
2 2
46. Kết quả của phép tính
10 6
2 5 12
là
A. 2 B.
2
C.
2
2
D.
3 2
2
47. Thực hiện phép tính
2 2
25 16
( 3 2) ( 3 2)
có kết quả:
A.
9 3 2
B.
2 9 3
C.
9 3 2
D.
3 2
48. Giá trị của biểu thức:
2
6 5 120
là:
A. 21 B.
11 6
C. 11 D. 0
49. Thực hiện phép tính
3 2 3
6 2 4
2 3 2
ta có kết quả:
A.
2 6
B.
6
C.
6
6
D.
6
6
50. Thực hiện phép tính
17 12 2
3 2 2
ta có kết quả
A.
3 2 2
B.
C.
D.
2 2
51. Thực hiện phép tính
4 2 3 4 2 3
ta có kết quả:
A.
2 3
B. 4 C. 2 D.
2 3
52. Thực hiện phép tính
2 2
3 2 2 3 3
ta có kết quả:
A.
3 3 1
B.
3 1
C.
5 3 3
D.
3 3 5
53. Thực hiện phép tính
3 3 3 3
1 1
3 1 3 1
ta có kết quả là:
A.
2 3
B.
2 3
C.
2
D. 2