- 1 -
Bài tập tự động hóa quá trình sản xuất(trang 12÷17)
1.1.2 Các khái niệm có liên quan đến hệ thống động học (tiếp theo)
Một phương trình vi phân cổ điển bao gồm các số hạng phụ thuộc vào biến số và
tổng ,hiệu đạo hàm của chúng tạo thành phương trình hàm số đầu vào. Đáp ứng của hệ có
thể đúng với điều kiện ban đầu hay sự biến thiên đầu vào. Một ví dụ về dạng phương
trình vi phân cổ điển dưới đây :
)(
0
2
2tfa
dt
dx
dt
xd =++
x(0-) = x0 (1.1)
dt
dx (0-) =
•
x0
Trong công thức trên x(t) là biến đáp ứng, ai là các hằng số phụ thuộc các tham số
của hệ. Hàm f(t) chứa các tác động bên ngoài (có thể là ngoại lực …) và x0 ,
•
x mô tả
trạng thái ban đầu và tốc độ ban đầu của hệ ngay tại thời điểm t=0. Chúng ta tính toán
hàm x(t) nhằm mô tả đáp ứng của hệ. Chú ý một biến số có dấu chấm ở phía trên miêu tả
việc lấy vi phân theo thời gian, do đó phương trình trên có thể được viết lại theo dạng sau
xaxax 01 ++
•••
= f(t) (1.2)
Ký hiệu 0- không thường được hay dùng tuy nhiên nó là điều kiện quan trọng để
xác định điều kiện ban đầu và giá trị đầu vào, ta coi đó là những gia trị ngay trước và sau
thời điểm t = 0.
Chúng ta cũng có thể sử dụng toán tử lấy đạo hàm D để miêu tả vi phân theo thời
gian (xem lại 1.6) :
D= dt
d (1.2)
Theo đó :
Dx= `dt
dx
D
2x= 2
2
dt
yd
Sử dụng toán tử lấy vi phân ,chúng ta có thể viết lại phương trình 1.2 như sau :
[D2 + a1D + a0]x(t) = f(t) (1.4)
Thông thường chúng ta hay miêu tả biến đáp ứng của hệ theo dạng chuẩn thông qua
đầu vào cũng như tỷ lệ giữa đầu ra - đầu vào. Với hệ tuyến tính, hàm truyền của nó được
định nghĩa là tỷ lệ giữa đầu ra với đầu vào của hệ với điều kiện biên ban đầu đã được xác
định qua biến đổi LapLace phương trình của hệ. Biến đổi Laplace (xem phụ lục F) của
phương trình 1.2 với điều kiện không ban đầu là :
[s2 + a1s + a0].X(s) = F(s) (1.5)
Biến đổi Laplace sẽ chuyển đổi phương trình của hệ từ một phương trình với biến
thời gian là độc lập thành một phương trình có biến s là biến độc lập. Kết quả mô tả
thông qua biến s sẽ tiện lợi hơn khi mô tả theo biến thời gian .
Giải phương trình (1.5) với tỷ lệ đầu ra - đầu vào cho ta hàm truyền của hệ :
- 2 -
01
2
1
)(
)(
asassF
sX
++
= (1.6)
Tỷ lệ đầu ra - đầu vào cũng có thể được viết thông qua ký hiệu theo biến thời gian
và sử dụng toán tử lấy vi phân D, sắp xếp lại phương trình (1.4) ta được :
01
2
1
)(
)(
aDaDtf
tx
++
= (1.7)
Trong biểu thức biến đổi Laplace thì phương trình (1.6) được sử dụng để định
nghĩa hàm truyền, ở công thức trên chúng ta tìm hàm truyền theo biến thời gian sẽ thuận
lợi hơn. Nếu vi phân của hàm f(t) xảy ra ở vế phải của phương trình vi phân thì tử số của
hàm truyền cũng chứa biến s (hay D) và chúng ta thường xem đó là tỷ lệ giữa hai đa thức
biến s ( D).
Phương trình vi phân trong không gian là tập hợp đồng thời của các phương trình vi
phân bậc nhất. Biến trạng thái là các biến phụ thuộc vào từng phương trình vi phân bậc
nhất và mô tả đáp ứng động học của hệ thống. Một ví dụ về phương trình vi phân trong
không gian được định nghĩa như sau :
•
x = a1x + a2y +f(t) (1.8a)
•
y = a3 .x.y.sin(x) + g(t) (1.8b)
•
z = a4.x.z + a5e-yt – h(t) (1.8c)
x(0) = x0
y(0) = y0
z(0) = z0
Bậc của phương trình vi phân hay hệ động học là số đạo hàm độc lập của hệ. Trong
một phương trình vi phân thông thường, bậc là hiệu của vi phân cấp cao nhất với vi phân
cấp thấp nhất trong phương trình. Phương trình (1.2) là phương trình bậc hai .
Trong tập hợp phương trình của một hệ, bậc của nó là số đạo hàm riêng của tất cả
các phương trình. Từ phương trình (1.8a) đến phương trình (1.8c) mô tả một hệ ba bậc .
Hàm số tuyến tính là hàm số có hai đặc điểm sau :
Nếu bạn nhân đối số của hàm với một hằng số thì giá trị của hàm số sẽ được
nhân lên bởi chính hằng số đó :
F(a.x) = a.F(x) (1.9)
Tổng giá trị hàm số đối với các biến bằng giá trị hàm số đối với tổng các biến
đó :
F(x1+x2) = F(x1) + F(x2) (1.10)
Chúng ta có thể kết hợp hai đặc tính trên như sau :
F(a
1x1+a2x2) = a1.F(x1) + a2.F(x2) (1.11)
Theo đó chỉ có hàm số tuyến tính là một đường thẳng đi qua gốc toạ độ; Dạng y =
m.x +b không phải là hàm tuyến tính tuân theo các điều kiện trên .
Một tổ hợp tuyến tính của các biến số được tạo ra từ tổng các tích của chúng. Ví dụ,
L = ax+by, ở đây a, b là các hằng số, là một tổ hợp tuyến tính của các biến x và y. Một
phương trình tuyến tính được tạo ra từ một tổ hợp tuyến tính và các đạo hàm của nó. Một
phương trình vi phân tuyến tính là một phương trình được tạo ra từ một tổ hợp tuyến tính
của các đạo hàm của các biến hệ thống. Ví dụ ,L = ax +b
•
x + c
••
x, ở đây a,b và c là các
- 3 -
hằng số, là phương trình vi phân tuyến tính, và các phương trình (1.1), (1.2), (1.8a) là các
phương trình vi phân tuyến tính hệ số hằng .
Một hệ tuyến tính được miêu tả bởi phương trình đại số tuyến tính và phương trình
vi phân tuyến tính. Trái lại một hệ phi tuyến bao gồm tổ hợp không tuyến tính của các
biến và đạo hàm. Ví dụ về các hàm phi tuyến là tích của các biến số như bình phương, lập
phương của các biến. Phương trình (1.8b) và (1.8c) là ví dụ về phương trình vi phân
không tuyến tính.
Nghiệm giải tích của phương trình vi phân là biểu thức toán học của các biến số
như một hàm phụ thuộc thời gian và có thể chứa các hàm mũ, hàm lượng giác sin (cos)
hay bất kì hàm nào khác. Giải một phương trình vi phân theo phương pháp giải tích đòi
hỏi phải có kiến thức về điều kiện ban đầu và đầu vào, nó như là hàm hiện của thời gian.
Nghiệm giải tích được tìm bằng cách tận dụng các kĩ thuật giải phương trình vi phân cổ
điển hay sử dụng kỹ thuật biến đổi Laplace (Xem phụ lục E và F để nắm bắt các phương
pháp trên) .
Việc tìm nghiệm phương trình vi phân tuyến tính có thể dễ dàng và các nghiệm giải
tích của chúng có thể dễ dàng tìm được bằng cách ứng dụng rộng rãi các phương pháp đã
được thừa nhận và được giới thiệu ở phần phương trình vi phân cơ bản. Ngược lại với hệ
phi tuyến, loại trừ các hệ bậc một ,chỉ xét tới các hệ có bậc từ hai trở lên không thể giải
bằng phương pháp giải tích. Nếu phương pháp giả tích là không khả thi với hệ phi tuyến
thì nghiệm số gần đúng của phương trình vi phân không tuyến tính có thể tìm được bằng
các phương pháp giả thiết gần đúng. Chúng ta gọi sự gần đúng là cách giải có sử dụng
máy điện toán .
Một đáp án có dùng tới máy điện toán của phương trình vi phân có thể tìm ra bằng
cách tích phân có sử dụng máy tính số. Tích phân số là một quá trình sử dụng tin học để
tính một nghiệm gần đúng về một số nguyên của một hàm số có chứa đạo hàm bằng
phương pháp số. Phương pháp phổ biến để tìm nghiệm phương trình vi phân là sử dụng
số gia nhỏ theo thời gian. Theo đó nghiệm của phương trình vi phân chỉ là những khoảng
thời gian rời rạc. Phương pháp có sử dụng máy điện toán nói chung là tận dụng để mô tả
trạng thái không gian của phương trình vi phân. Nói chung tính toán đáp ứng của một hệ
thống động học theo cách này gọi là mô phỏng số (phương pháp số) .
Trong cách tính tương tự thì phương trình vi phân được mô tả bởi một mối quan hệ
tuyến tính hay phi tuyến của các thành phần điện và máy tích phân điện tử (tính toán
khuyếch đại các thông tin phản hồi). Từ đó phương trình điều khiển hệ thống điện cũng
như các phương trình điều khiển hệ thống động học đều được xem xét kĩ lưỡng, khi có
một tín hiệu tương tự được thiết lập giữa hai hệ thống. Máy tích phân điện tử có thể giải
được phương trình vi phân bằng cách thực hiện các hoạt động động học về điện tương
ứng để cho hệ thống có thể hiểu được. Rất nhiều hệ thông có thể mô phỏng bằng cách tạo
ra tín hiệu tương tự giữa tín hiệu hiển thị là Vol(v) của một máy tính tương tự và nghiệm
của phương trình vi phân được giải .
1.2 Mô hình hoá hệ thống động học
1.2.1 Các bước trong quá trình mô hình hoá và mô tả hệ thống động học
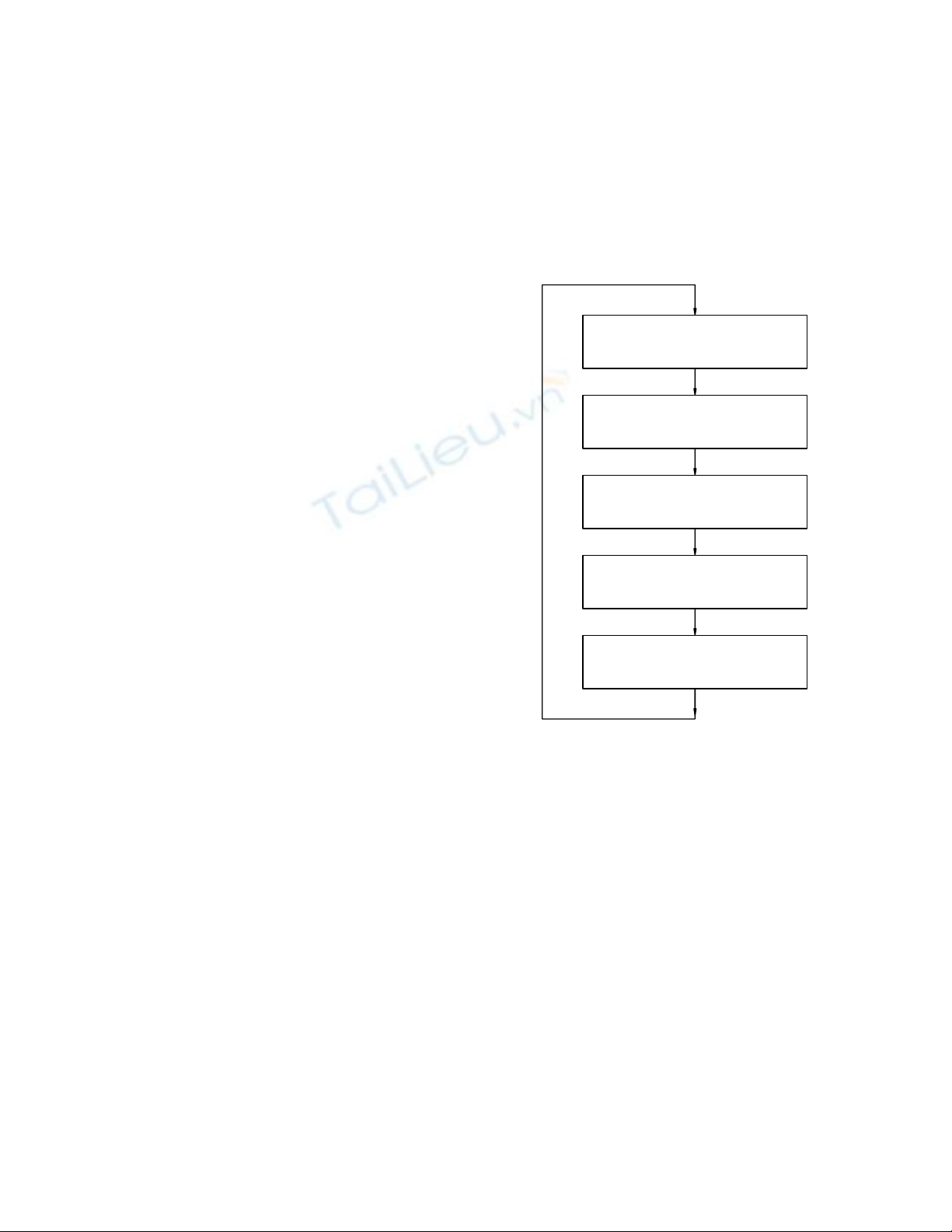
Hình 1.5 minh hoạ một vài giai đoạn liên quan đến mô hình hoá hệ thông động học.
Bước đầu tiên là quan tâm tới hệ thông động học thực tế. Nó phải có tất cả các đáp ứng
động học tiêu biểu tương ứng một cách chính xác với hoạt động của hệ tuyến tính hay phi
- 4 -
tuyến và các quan hệ động học mặc nhiên xuất hiện của hệ thống .Hệ thống thực tế, tất
nhiên là phải có những đáp ứng thực tế mà chúng ta cần xác định .
Bước hai là sự nhận thức của người thiết kế về hệ thống và các thành phần động
học tiêu biểu của nó. Mô hình này có thể bỏ qua một số các thành phần phi tuyến hay các
thành phần động học bậc cao nhằm đơn giản hoá. Tuy nhiên hệ thống thực phải chứa tất
cả các tác động và các bộ phận cấu thành. Về việc này sự nhận thức của người thiết kế có
thể không miêu tả đúng một hệ thống thực.
Bước ba là mô hình hoá toán học hệ thống
bằng phương trình vi phân nhận được từ việc bảo
toàn các đặc tính theo một quy tắc phù hợp. Nếu hệ
là tuyến tính thì việc phát triển mô hình toán học
phù hợp là khá dễ dàng. Tuy nhiên nếu hệ là phi
tuyến thì mô hình toán học sẽ chứa các phép xấp xỉ
nhằm đơn giản hóa thuật toán. Về điều này phương
trình có thể miêu tả không chính xác nhận thức của
người thiết kế về hệ thống hiện tại .
Bước bốn là tính toán đáp ứng của hệ thống
.Đáp ứng của hệ mô tả bằng phương pháp giải tích
là lời giải chính xác của phương trình. Dù vậy vẫn
tồn tại một vài lỗi nhỏ giữa đáp ứng được tìm theo
phương pháp số hay phương pháp tương tự và
nghiệm thực của phương trình
Bước thứ năm liên quan đến việc phân tích
quá trình thực hiên của hệ thống được thể hiện qua
những đại lượng đo lường đặc trưng. Điều này bàn
đến phương pháp phân tích tần số và thời gian của
hệ để đánh giá hoạt động của hệ .
Một trong những trách nhiệm quan trọng nhất của người thiết kế là quá trình kiểm
tra sự kết hợp các trị số của các thành phần xác định hoạt động của hệ và điều khiển trị số
của các thành phần cho tới khi đạt được hoạt động mong muốn. Các thủ tục giảm và kiểm
tra có thể được thực hiện bằng cách lắp ráp phần cứng hay bằng mô hình toán. Cái thuận
lợi của mô hình hoá và phân tích toán học là thường nhanh hơn và không đắt bằng thử
nghiêm với các phần cứng. Theo đó quá trình lặp lại ở hình (1.5) trong đó hệ thống được
chỉnh sửa lại là một phần quan trọng của quá trình thiết kế .
Một điều quan trọng cần chú ý rằng vì mô hình hoá có thể đơn giản (bằng cách bỏ
đi các thành phần phi tuyến và bậc cao) hay xấp xỉ, việc tính toán đáp ứng hệ thống từ
nghiệm giải tích của phương trình vi phân có thể bỏ qua trong quá trình tính đáp ứng của
hệ. Nếu mô hình toán học có chứa phép xấp xỉ thì tìm nghiệm giải tích là hai bước đã
được thực hiện trong quá trình xác định đáp ứng của hệ thống hiện tại .
Khi đáp ứng được tìm bằng mô phỏng số hay mô phỏng tương tự thì đã thực hiện
được ba bước trong đáp ứng của hệ thống hiện tại, từ đây có thể có một vài sai lệch trong
việc tính tích phân hay các đáp ứng điện và mô hình toán học có thể không chứa các hệ
thống có bậc cao hơn .
VËt thÓ cã thËt
HÖ thèng ®éng häc
M« h×nh cña sù nhËn
thøc vÒ hÖ thèng
BiÓu diÔn to¸n häc
TÝnh to¸n ®¸p øng
Ph©n tÝch ho¹t ®éng
H×nh 1.5
- 5 -
Khi ta nói đến “ hệ thống “ tức là đề cập đến hệ thống có thực hay mô hình toán
học của hệ thống đó. Thông thường khi đề cập đến “đáp ứng của hệ thống” có nghĩa là ta
nói tới đáp ứng của hệ thống thực hay sự tính toán hoặc mô phỏng đáp ứng của hệ thống.
Chúng ta cần phải chú ý tới sự khác biệt trên .
Mô hình hoá hệ thống ,tính toán đáp ứng của hệ ,phân tích hoạt động của hệ thống
và thiết kế lại hệ thống cho phù hợp là các phần trong chu trình hoàn thành một công cụ
khoa học. Trừ các phần lí thuyết trìu tượng, không có bước đơn lẻ nào có giá trị nếu
không hoàn thành theo chu trình đó. Sau khi quá trình trên hoàn tất nêu đáp ứng của hệ
thống không hiển thị được thì hệ và mô hình của nó cần phải sửa chữa và các thành phần
đang tồn tại cũng phải điều chỉnh lại theo đầu ra của hệ thống .
1.2.2 Tiện ích của việc mô phỏng và mô hình hoá hệ thống
Thuận lợi chủ yếu của mô hình hoá một hệ thống và phân tích đáp ứng của nó là
cho phép ta biết trước hoạt động của nó trước khi tạo ra nó. Điều này đôi khi gọi là
“nguyên mẫu thực”. Chúng ta cũng có thể phân tích hoạt động của một hệ thống đã tồn
tại nhằm cải tiến những hoạt động tĩnh hay động của hệ thống hay chúng ta có thể xác
định điều gì xảy ra với hệ khi điều đầu vào khác thường hoặc xác định những điều kiện
không làm cho hệ thống thực bị nguy hiểm .
Ví dụ nếu chúng ta đang thiết kế một hệ thống mới và muốn có được mức độ hoạt
động chính xác, chúng ta có thể lựa chọn những thành phần có kích thước chính xác để
cho ta kết quả mong muốn. Mặt khác nếu hệ thống đã tồn tại và ta muốn cải tiến hoạt
động của nó ,mô hình hoá và phân tích sẽ giúp ta xác định những thành phần nào có thể
thay đổi và khoảng thay đổi cần thiết. Nếu chúng ta muốn giảm các thành phần tiêu biểu
của hệ, mô hình hoá không chỉ giúp ta biết được thành phần nào ảnh hương đến mà còn
chỉ cho ta biết làm như nào để thay đổi chúng sao cho đạt được kết quả mong muốn. Nếu
chúng ta đã tìm hiểu về những gì sẽ xảy ra đối với hệ thống khi đầu vào hay điều kiện
khác thường như sự không hoạt động của động cơ thuỷ lực phụ trên hệ thông điều khiển
của máy bay hay một phương tiện đường không sau đó mô hình hoá và phân tích nó sẽ
không làm cho chúng ta mất nhiều triệu $ khi rủi ro trong việc xác định trạng thái hoạt
động của hệ thống .
Một mô hình toán học tốt của hệ thống động học là có thể cung cấp ngay cho chúng
ta hoạt động của các bộ phận cấu thành nên hệ thống và các thành phần động học tiêu
biểu mà không phải phân tích nhiều. Nếu chúng ta gặp những thành phần động học tiêu
biểu quen thuộc thì ta có thể đoán nhận được đáp ứng của hệ thống, đủ truyền đạt những
gì cần biết của chúng ta về đáp ứng của hệ, hay ta muốn tính toán tần số và đáp ứng thời
gian của hệ để cung cấp thêm những hiểu biết rõ về nó .
Tất nhiên nghiệm của phương trình vi phân có thể không mô tả chính xác hệ thống
thực tế một cách rõ ràng, mặc dù vậy thì việc mô phỏng cũng chỉ ra được phương hướng
của đáp ứng để chúng ta có thể biết được thành phần nào thay đổi được hay xấp xỉ chúng
như thế nào để cho ta kết quả mong muốn .