BÀI TOÁN SO SÁNH M R NGỞ Ộ
§ 1. SO SÁNH NHI U T L Ề Ỷ Ệ
Trong ch ng tr c chúng ta đã xét bài toán so sánh t l cáươ ướ ỷ ệ
th có đc tính A trong hai t p h p chính. b y gi chúng ta s mể ặ ậ ợ ấ ờ ẽ ở
r ng bài toán này b ng cách xét bài toán so sánh đng th i t l cáộ ằ ồ ờ ỷ ệ
th có đc tính A gi a nhi u t p h p chính.ể ặ ữ ề ậ ợ
Gi s ta có k t p h p chính Hả ử ậ ợ 1, H2,... Hk. M i cá th c aỗ ể ủ
chúng có th mang hay không mang đc tính A.ể ặ
G i pọ1 là t l có th mang đc tính A trong t p h p chínhỷ ệ ể ặ ậ ợ
Hi (i = 1, 2, ...k).
Các t l này đc g i là các t l lý thuy t mà chúng ta ch aỷ ệ ượ ọ ỷ ệ ế ư
bi t.ế
Ta mu n ki m đnh gi thi t sau:ố ể ị ả ế
Ho: p1 = p2 = ... = pk (t t c các t l này b ng nhau).ấ ả ỷ ệ ằ
T m i t p h p chính ừ ỗ ậ ợ Hi ta rút ra m t ng u nhiên có kíchộ ẫ
th c nướ i, trong đó chúng ta th y có mấi cá th mang đc tính A. các dể ặ ữ
li u này đc trình bày trong b ng sau đây:ệ ượ ả
M uẫ1 2 ... k T ngổ
Có A m1m2... mkm
Không
A
l1l2... lkl
T ng ổn1n2... nkN = m + l =
ni
N u gi thi tế ả ế
Ho: p1 = p2 = ... = pk = p
1

Là đúng thì t l chung p đc c l ng b ng t s gi a sỷ ệ ượ ướ ượ ằ ỷ ố ữ ố
cá th đc tính A c a toàn b k m u g p l i trên t ng s cá th c aể ặ ủ ộ ẫ ộ ạ ổ ố ể ủ
k m u g p l i.ẫ ộ ạ
$
m
pN
=
T l cá th không có đc tính A đc c l ng b iỷ ệ ể ặ ượ ướ ượ ở
$ $
l
q 1 p N
= − =
Khi đó s cá th có đc tính A trong m u th i (m u rút t t pố ể ặ ẫ ứ ẫ ừ ậ
h p chính ợHi) s x p x b ngẽ ấ ỉ ằ
ᄉ
$
i
ii
n m
m n p N
= =
và s cá th không có đc tính A trong m u th i s x p x b ngố ể ặ ẫ ứ ẽ ấ ỉ ằ
$
ii i l
i n q n N
= =
$
Các s ố
ᄉ
i
m
và
i
i
$
đc g i là các t n s lý thuy t (TSLT), cònượ ọ ầ ố ế
các s mối, li đc g i là các t n s quan sát (TSQS).ượ ọ ầ ố
Ta quy t đnh bác b Hế ị ỏ o khi TSLT cách xa TSQS m t cáchộ
“b t th ng”. Kho ng cách gi a TSQS và TSLT đc đo b ng testấ ườ ả ữ ượ ằ
th ng kê sau đây:ố
ᄉ
( )
ᄉ
( )
22
k k
ii
ii
i
i
i 1 i 1
m m l l
Tl
m
= =
−−
= +
� � $
$
Ng i ta ch ng minh đc r ng n u Hườ ứ ượ ằ ế o đúng và các t n s lýầ ố
thuy t không nh thua 5 thì T s có phân b x p x phân b ế ỏ ẽ ố ấ ỉ ố
2
χ
v iớ
k – 1 b c t do. Thành th mi n bác b Hậ ự ử ề ỏ o có d ng {T > c}, đó cạ ở
đc tìm t đi u ki n P{T > c} = ượ ừ ề ệ . V y c chính là phân v m c ậ ị ứ
c a phân b ủ ố
2
χ
v i k – 1 b c t doớ ậ ự .
Chú ý. Test th ng kê T có th bi n đi nh sau.ố ể ế ổ ư
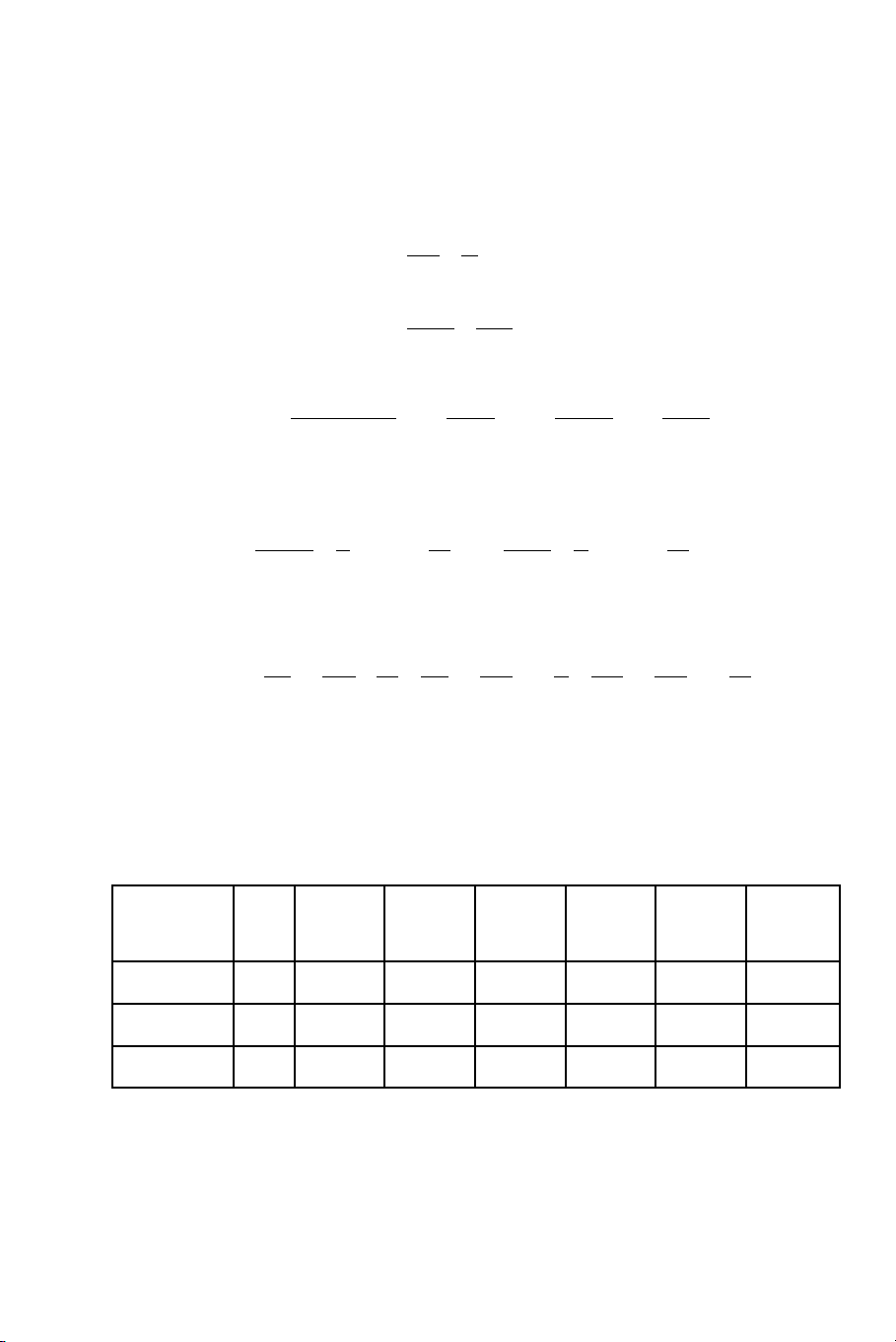
Ta có:
2
( )
$
( )
$
( )
ᄉ
( )
22
2 2
i i
i i i i i i i
l l n m n 1 p m n p m m
� �
− = − − − = − = −
� �
$
Do đó
ᄉ
( )
ᄉ
ᄉ
( )
$ $
ᄉ
( )
$ $
ᄉ
$
ᄉ
$
2
i
ii
1
2
i
ii i
1
22
k2
i
iio
i i
i 1 i i i i
1 1
T m m l
m
1 1
m m n p n q
m m m m m m
2
n pq n pq n pq n pq
=
� �
= − +
� �
� �
� �
= − +
� �
� �
� �
−
= = − +
� � � �
$
Chú ý r ng ằ
ᄉ
$ $ $
ᄉ
$ $
ᄉ
$
;
2
i1
ii
i
i i
m m 1 m m 1 m
m m
n pq q q n pq q q
= = = =
� � � �
V y ậ
$ $ $
$
$
2 2 2
2
i i i
i i i
m m m
1 m 1 p N m
T N N
n n ml n l
pq q pq q
= − = − = −
� � �
N u s d ng công th c này ta s không c n tính các t n s lýế ử ụ ứ ẽ ầ ầ ố
thuy t, do đó nó đc dùng trong th c hành.ế ượ ự
Ví d 1.ụ So sánh tác d ng c a 6 m u thu c th nghi m trên 6ụ ủ ẫ ố ử ệ
lô chu t, k t qu thu đc nh sau:ộ ế ả ượ ư
M uẫ
thu cố
1 2 3 4 5 6 T ngổ
S s ngố ố 79 82 77 83 76 81 478
S ch tố ế 21 18 23 17 24 19 122
T ng ổ100 100 100 100 100 100 600
Ta mu n ki m đnh gi thi tố ể ị ả ế
Ho: T l ch t trong 6 m u thu c là nh nhauỷ ệ ế ẫ ố ư
Đi thi tố ế H1: T l ch t trong 6 m u thu c là khác nhauỷ ệ ế ẫ ố
3
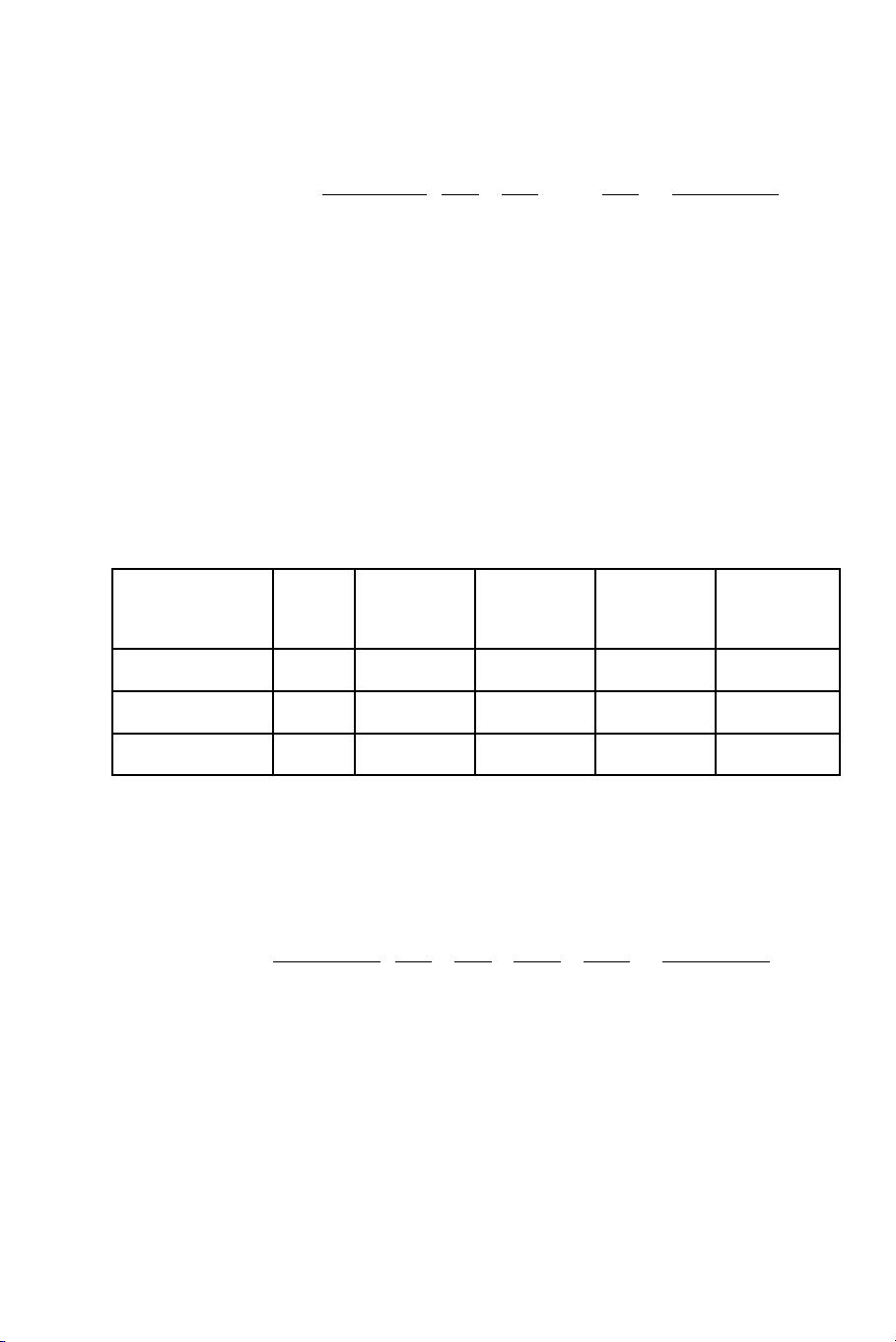
Gi i ả
Ta có
� �
= + + + −
� �
� �
L
2 2 2 2
600 79 82 81 (600)(478)
T(478)(122) 100 100 100 122
= − =2353,24 2350,81 2,42
V i m c ý nghĩa ớ ứ = 5%, tra b ng phân b ả ố
χ
2
v i 5 b c t do taớ ậ ự
có
χ =
2
0,05 11,07
Vì T < c nên ta ch p nh n Hấ ậ o. J
Ví d 2.ụ Có 4 th y giáo A, B, C, D cùng d y m t giáo trìnhầ ạ ộ
th ng kê. Ban ch nhi m khoa mu n tìm hi u ch t l ng d y c a 4ố ủ ệ ố ể ấ ượ ạ ủ
th y này nên đã làm m t cu c kh o sát. K t qu nh sau:ầ ộ ộ ả ế ả ư
Th y ầ
K t quế ả A B C D T ngổ
Đt ạ60 75 150 125 410
Không đtạ40 75 50 75 240
T ng ổ100 150 200 200 650
V i m c ý nghĩa ớ ứ = 0,01 có th cho r ng t l h c sinh để ằ ỷ ệ ọ ỗ
trong các h c sinh đã h c các th y trên là nh nhau hay không?ọ ọ ầ ư
Gi i.ả Ta có
� �
= + + + −
� �
� �
= − =
2 2 2 2 2
(650) 60 75 150 125 (650)(410)
T(410)(240) 100 150 200 200 240
1134,07 1110,41 23,65
S b c t do là 3 và ố ậ ự
χ =
2
0,01 11,343
. Vì T > c nên ta bác b giỏ ả
thuy t Hếo. T l h c sinh đ c a các th y A, B, C, D nh nhau.ỳ ệ ọ ỗ ủ ầ ư
§ 2. SO SÁNH CÁC PHÂN S Ố
Xét m t b ộ ộ A g m r tính tr ng, ồ ạ A = (A1, A2, ...Ar), trong đó m iỗ
cá th c a t p h p chính ể ủ ậ ợ H có và ch có m t trong các tính tr ngỉ ộ ạ
4

(hay ph m trù) Aại.
G i pọi (i = 1, 2, ... r) là t l cá th tính tr ng Aỷ ệ ể ạ i trong t pậ
h p chính H. Khi đó véct ợ ơ = (p1, p2, ...pr) đc g i là phân bượ ọ ố
c a ủA trong t p h p chính H.ậ ợ
Ch ng h n, m i ng i đi làm có th s d ng m t trong cácẳ ạ ọ ườ ể ử ụ ộ
ph ng ti n sau: đi b , đi xe đp, đi xe máy, đi xe buýt. Trongươ ệ ộ ạ
thành ph X có 18% đi b , 32% đi xe đp, 40% đi xe máy và 10%ố ộ ạ
đi xe buýt. Nh v y ư ậ = (0,18; 0,32; 0,4; 0,1) là phân b c a cáchố ủ
đi làm (A ) trong t p h p các dân c c a thành ph X.ậ ợ ư ủ ố
T ng t m i ng i có th đc x p vào 1 trong 3 ph mươ ự ỗ ườ ể ượ ế ạ
trù sau: r t h nh phúc, b t h nh, ho c có th đc x p vào 1ấ ạ ấ ạ ặ ể ượ ế
trong 3 l p sau: d i 25 tu i, trong kho ng t 25 đn 45 tu i,ớ ướ ổ ả ừ ế ổ
trên 45 tu i... có th d n ra r t nhi u ví d t ng t nh v y.ổ ể ẫ ấ ề ụ ươ ự ư ậ
Gi s (pả ử 1, p2,...pr) là phân b c a (Aố ủ 1, A2,...Ar) trong t pậ
h p chính H và (qợ1, q2,...qr) là phân b c a ố ủ A = (A1, A2,...Ar) trong
t p h p chính Y. Ta nói (Aậ ợ 1, A2...Ar) có phân b nh nhau trongố ư
X và Y n u (pế1, p2,...pr) = (q1, q2,...rr) p1 = q1,...pr = qr.
Chúng ta mu n ki m đnh xem ố ể ị A = (A1, A2,...Ar) có cùng
phân s trong X và Y hay không d a trên các m u ng u nhiên rútố ự ẫ ẫ
t X và Y.ừ
T ng quát h n, gi s ta có k t p h p chính Hổ ơ ả ử ậ ợ 1, H2,...Hk.
G i ọ
( )
π = K
i i i i
1 2 r
p ,p , p
là phân b c a ố ủ A = (A1, A2,...Ar) trong t pậ
h p chính Hợi.
Ta mu n ki m đnh gi thuy t sauố ể ị ả ế
π = π = = πK
1 2 k
o
H :
(Các phân b này là nh nhau trên cácố ư
t p h p chính Hậ ợ i).
Chú ý r ng Hằo t ng đng v i h đng th c sau:ươ ươ ớ ệ ẳ ứ
= = =
= = =
= = =
= = =
K
K
K
K
1 2 k
1 1 1
1 2 k
2 2 2
1 2 k
i i i
1 2 k
r r r
p p p
p p p
p p p
p p p
5


























