
1
NHIỀUCÁCHGIẢICHOMỘTBÀITOÁNTHCS
Trongtoánhọccórấtnhiềubàitoáncórấtnhiềucáchgiải.Vớibàiviếtnàytácgiảxinđượcđềcậpđếnmộtsố
cáchgiảibàitoáncấpTHCSthôngquaviệcvẽđườngphụ,Đâylàcáccáchgiảiđượckhaitháctheocáchướng
khácnhautrêncơsởtính chấtđườngtrungbìnhcủatamgiác,nhằmpháthuytínhsángtạochohọcsinhnhằm
giúpcácemhứngthúhơntrongviệchọcvàlàmtoán.Tácgiảbàiviếtmongnhậnđượcsựđónggópýkiến,
nhậnxétcủacácthầycô,bạnđọctrongcảnướcnhằmngàycànghoànthiệnhơn.
Bàitoán:ChotamgiácABCcântạiA,đườngtrungtuyếnCD.TrêntiađốicủatiaBAlấyđiểmK
saochoBK=BA.Chứngminhrằng CD= 1
2CK(1)
Giải:Ởđâyxinđượcgiớithiệu 10cáchgiảibàitoántrên.
Cách1:(Hình 1)
GọiElàtrungđiểmcủaAC.
CóBElàđườngtrungbìnhcủa DAKC=>BE= 1
2KC(1)
Xét DBDCvà DCEBcó:
BD=CE(vìBD= 1
2AB;CE= 1
2ACmàAB=AC); Cạnh BCchung;
·
·
DBC ECB = (vì DABCcântạiA);
Vậy DBDC= DCEB(c.g.c);
SuyraCD=BE(haicạnhtươngứng)(2)
Từ(1)và(2)suyraCD= 1
2CK(đ.p.c.m)
Cách2: (Hình2)
GọiHlàtrungđiểmcủaKC.BHlàđườngtrungbìnhcủa DAKC=>BH= 1
2AC
Xét DBDCvà DBHCcó:
BD=BH(vìBD= 1
2AB;BH= 1
2ACmàAB=AC);
·
·
HBC DBC = vì
· · ·
·
DBC ACB mµ ACB HBC (do so le trong, BH//AC) = =;
BCcạnhchung;
Vậy DBDC= DBHC(c.g.c)
SuyraCH=DC(haicạnhtươngứng);(1)
MàHlàtrungđiểmcủaKCnênCH= 1
2CK(2).
Từ(1)và(2)suyra:CD= 1
2CK.
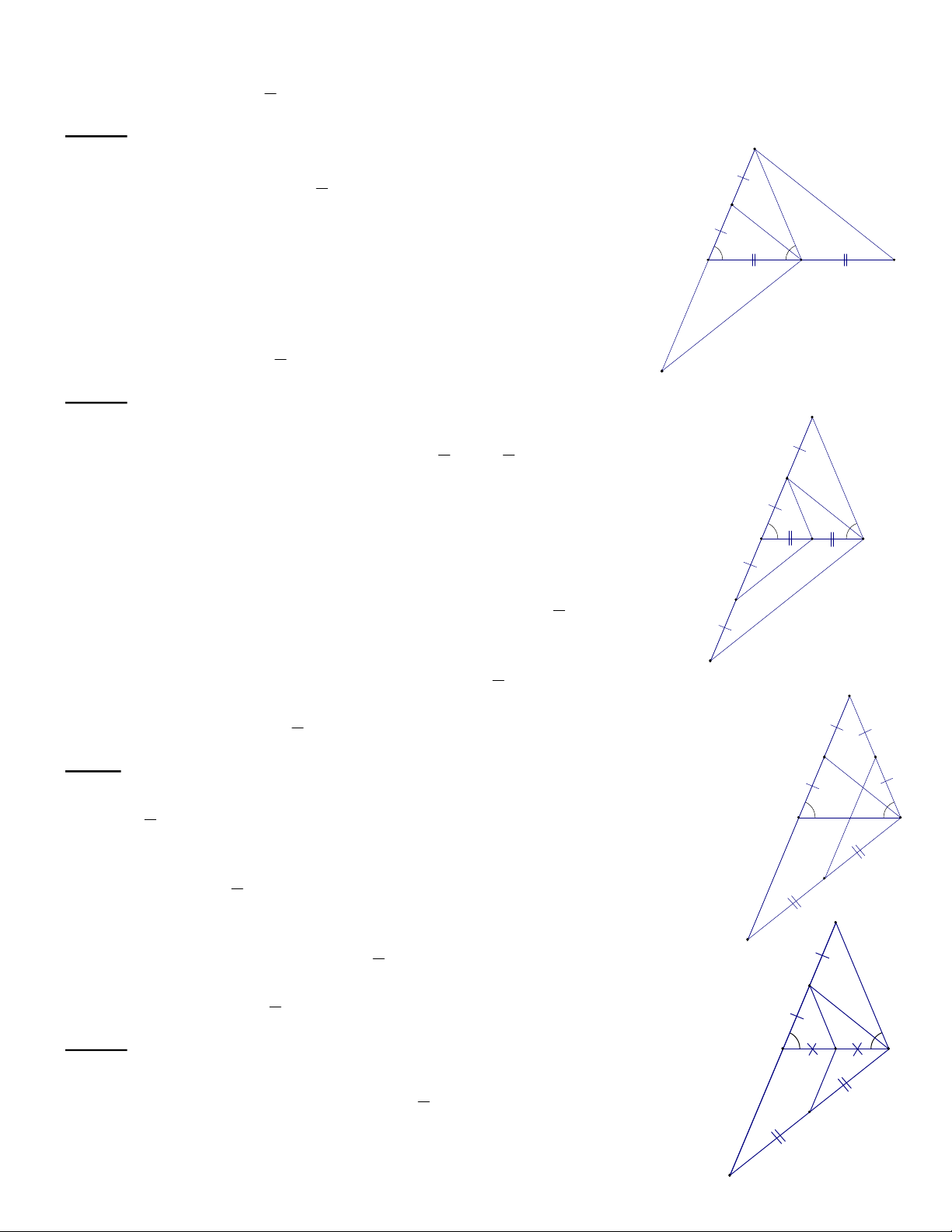
Cách3: (hìnhbên)
TrêntiađốicủatiaCAlấyđiểm MsaochoCA=CM;CDlàđường
trungbìnhcủa DABM=>DC= 1
2BM (1) Xét DKBCvà DMCBcó:
BCcạnhchung;
·
·
KBC MCB =(cùng bùvới
·
ABC );
(1) TríchNângcaovàphát triểntoán7Nhà xuất bảnGiáodục.
H.1
E
K
D
B C
A
H.2
H
K
D
B C
A
M
K
D
B C
A
2
KB=MC(vìKB=AB;MC=AC;AB=AC);
Vậy DKBC= DMCB(c.g.c)=>KC=MB(haicạnhtươngứng)(2).
Từ(1)và(2)suyraDC= 1
2CK. (đ.p.c.m);
Cách4: (hình4)
TrêntiađốicủatiaCBlấyđiểmNsaochoCB=CN; Tacó: DClàđường
trungbìnhcủa DABN=>CD= 1
2AN (1);
Xét DKBCvà DACNcó:
BC=CN;
·
·
KBC ACN =
· ·
·
·
·
·
0 0
(v× KBC 180 ABC; ACN 180 ACB mµ ABC ACB) = - = - =
KB=AC(cùngbằngAB);
Vậy DKBC= DACN(c.g.c)=>CK=AN (haicạnhtươngứng) (2);
Từ(1)và(2)suyra: CD= 1
2CK.(đ.p.c.m);
Cách5: (hình5)
GọiP;QlầnlượtlàtrungđiểmcủaBCvàBK;
CóDPlàđườngtrungbìnhcủa DABC=>DP= 1 1
AC = AB = DB
2 2;
DP//AC=>
·
·
DPB ACP = (cùngbùvới
·
DPC );Theogiảthiết
·
·
ABC ACB =
(DABCcântại A);
·
·
DPB DBP = mà
· ·
0
QBP 180 DBP = -;
·
·
0
DPC 180 DPB = - =>
·
·
QBP DPC =
Xét DQBPvà DDPCcó:
QB=DP;
·
·
QBP DPC =(chứngminhtrên);BP=CP(cùngbằng 1
2BC);
Vậy DQBP= DDPC(c.g.c)=>DC=QB (1);
MặtkhácQPlàđườngtrungbìnhcủa DKBCnênQP= 1
2CK(2);
Từ(1)và(2)suyra:CD= 1
2CK(đ.p.c.m);
Cách6: (Hình6).
GọiE;OlầnlượtlàtrungđiểmcủaACvàKC;OElàđườngtrungbìnhcủa DACK
nênOE= 1
2AKmàAK=2AB=2AC=>OE=AB=AC;
Xét DCDAvà DOCEcó:
AD=CE(cùngbằng 1
2AC);OE=CA;
·
·
DAC CEO = (đồngvị,OE//AD);
Vậy DCDA= DOCE(c.g.c)=>OC=CD; (1)
MặtkhácOlàtrungđiểmCKnênOC= 1
2CK(2)
Từ(1)và(2)suyraCD= 1
2CK.(đ.p.c.m);
Cách7: (hình7)
GọiP;OlầnlượtlàtrungđiểmcủaBCvàCK;
DPlàđườngtrungbìnhcủa DABCnênDP= 1
2AC
H.4
N
K
D
B C
A
H.5
Q
K
D
P
B C
A
H.6
O
E
K
D
B C
A
H.7
O
K
D
P
B C
A

3
OPlàđườngtrungbìnhcủa DCBKnênOP= 1
2BK
Theobài ra,tacóBK=ACnênDP=OP;
·
· ·
· ·
· · ·
· ·
OPB DBP (so le trong, OP//DB); DBP ACP vµ ACP DPB OPB DPB OPC DPC = = = Þ = Þ =
Xét DDPCvà DOPCcó:
DP=OP(c/mtrên);
· ·
OPC DPC = (c/mtrên);
Cạnh PCchung
Vậy DDPC= DOPC(c.g.c)=>OC=CDmàOC= 1
2CK=>CD= 1
2CK. (đ.p.c.m).
Cách8: (hình8)
TrêntiađốicủatiaDClấyđiểmFsaochoDF=DC;
Xét DBDFvà DADCcó:
DF=DC;DA=DB;
·
·
FDB CDA = (haigócđốiđỉnh);
suyra: DBDF= DADC(c.g.c)=>BF=ACmàAC=BKnênBF=BK;
Talạicó:
·
·
0
FBC ACB 180 (BF // AC nªn hai gãc trong cïng phÝa bï nhau); + =
· ·
0
KBC ABC 180 (hai gãc kÒ bï) + =
mà
·
·
ABC ACB ( ABC c©n t¹i A) = D=>
·
·
KBC FBC =
Xét DFBCvà DKBCcó:
FB=KB(c/mtrên);
·
·
KBC FBC = ;
BCcạnhchung;
Vậy DFBC= DKBC(c.g.c)=>FC=CK=>2CD=CK=>CD= 1
2CK.(đ.p.c.m);
Cách9:(hình 9);
TừBkẻđường thẳng songsongvớiCKcắtACtạiO;TừCkẻđường
thẳng songsongvớiBKcắtBOkéodàitạiR;
Dễdàng chứngminhđược CR=BK=AB;BR=CK;
Xét DROCvà DBOAcó:
· ·
CRO ABO (so le trong, CR//AB) =;CR=AB;
·
·
RCO BAO (so le trong, CR//AB) =Suyra: DROC= DBOA(g.c.g);
=>OA=OC= 1
2AC== 1
2AB;OB=OR;=>OR= 1
2BR= 1
2CK;(1);
Xét DADCvà DCORcó:
AD=OC(cùngbằng 1
2AB);
·
·
RCO DAO (so le trong, CR//AB) =;
CR=AC(cùngbằngAB);
Vậy DADC= DCOR(c.g.c);=>OR=CD (2);
Từ(1)và(2)=>CD= 1
2CK.(đ.p.c.m);
Cách10: (hình10)
H.8
F
K
D
B C
A
H.9
R
O
K
D
B C
A

4
TrêntiađốicủatiaBClấyđiểmFsaochoBF=BC;NốiFK;GọiIlàtrung
điểmcủaFK;
Xét DFBKvà DCBAcó:
FB=CB;
·
·
FBK CBA (hai gãc ®èi ®Ønh); =AB=KB(giảthiết);
nên DFBK= DCBA(c.g.c)=>FK=AC
màAB=AC=>FK=AB=> 1
2FK= 1
2AB
=>FI=DB;(1)
Theobài ra,tacó:
·
·
·
· ·
·
·
ACB ABC mµ ACB = BFI BFI = ABC = DBC = Þ
(2)
Xét DFBIvà DBCDcó:
FB=BC;
·
·
BFI = DBC (theo(2));
FI=BD (theo(1));
Vậy DFBI= DBCD(c.g.c)=>BI=CD(3);
MặtkhácdoI;BlầnlượtlàtrungđiểmcủaFKvàFC=>IBlàđườngtrungbìnhcủa DKFC
=>BI= 1
2CK(4);Từ(3)và(4)suyra:CD= 1
2CK.(đ.p.c.m);
Chúý:Trongcáccáchvẽđườngphụ,cóthểlậpluậntheonhiềucáchkhácnhauđểchứngminhđược
CD= 1
2CK.
NguyễnVănChương
Trường THCSNguyễnHàm Ninh
BaĐồnQuảng TrạchQuảng Bình
Điệnthoại:0935187009
H.10
I
F
K
D
B C
A

























![Bài tập so sánh hơn và so sánh nhất của tính từ [kèm đáp án/mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250808/nhatlinhluong27@gmail.com/135x160/77671754900604.jpg)
![Tài liệu tham khảo Tiếng Anh lớp 8 [mới nhất/hay nhất/chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250806/anhvan.knndl.htc@gmail.com/135x160/54311754535084.jpg)




![Tài liệu Lý thuyết và Bài tập Tiếng Anh lớp 6 [Mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250802/hoihoangdang@gmail.com/135x160/18041754292798.jpg)




