
CÁC Đ ÔN T P THI H C KỲ 1Ề Ậ Ọ
*********
Đ 1:ề
Câu 1 (2,0 đi m)ể
Cho hàm s : ố
1
1 1
yx x
=+ + −
a) Tìm t p xác đ nh c a hàm s .ậ ị ủ ố
b) Xác đ nh tính ch n, l c a hàm s .ị ẵ ẻ ủ ố
Câu 2 (1,5 đi m) ể
Không dùng máy tính c m tay, hãy gi i h ph ng trình sau:ầ ả ệ ươ
2 3 4
2 4 2
3 4 0
x y z
x y z
x y z
+ + =
+ + = −
− + =
Câu 3 (2,0 đi m)ể
Cho ph ng trình ươ
2
( 1) ( 1) 0m x m m− + − =
(1) , v i tham s ớ ố
m R∈
.
a) Gi i ph ng trình (1) khi ả ươ
2m=
.
b) Gi i và bi n lu n ph ng trình (1) theo tham s ả ệ ậ ươ ố
m
.
Câu 4 (3,5 đi m)ể
Cho tam giác
ABC
v i ớ
( 7;5), (5;5), (1;1)A B C−
.
a) Tìm t a đ trung đi m ọ ộ ể
I
c a đo n th ng ủ ạ ẳ
AB
.
b) Tìm t a đ đi m ọ ộ ể
M
th a mãn h th c ỏ ệ ứ
2AM M B=
uuur uuur
.
c) Ch ng minh ứ
1 2
3 3
CM CA CB= +
uuur uuur uuur
.
d) Ch ng minh ứ
CM AB⊥
.
e) Tính góc B c a tam giác ủ
.ABC
Câu 5 (1,0 đi m)ể
Tìm giá tr nh nh t c a hàm s ị ỏ ấ ủ ố
2
2 1
x
yx
= + −
v i ớ
1x>
.
--------------------------------------------------------------------------------------------
Đ 2:ề
I .PH N CHUNG CHO C HAI BAN ( 7,0 đi m )Ầ Ả ể
Bài 1 ( 1 đi m )ể

Cho A =
[ ]
2;3−
(
]
( )
4;4;2 ∞−=−= CB
Tìm
,,, BACBABA C∩∪∩
A\ B
Bài 2 ( 2 đi m ) ểCho hàm s y = axố2 – bx + 1 (1)
a / Xác đ nh hàm s (1) bi t r ng đ th c a hàm s đó là parabol cóị ố ế ằ ồ ị ủ ố
đ nh I ( 2;- 3)ỉ
b / Xét s bi n thiên và v đ th c a hàm s y = xự ế ẽ ồ ị ủ ố 2 - 4x + 1.
Bài 3 ( 2 đi m ) ể Gi i ph ng trình:ả ươ
a) b)
Bài 4 (2 điểm ) Trong m t ph ng t a đ (Oxy) cho 4 đi m A, B, C, Dặ ẳ ọ ộ ể
g i M, N l n l t là trung đi m c a AB và CD . G i I là trung đi m c aọ ầ ượ ể ủ ọ ể ủ
MN.
a/Ch ng minh ứ
0=+++ IDICIBIA
b/Cho A(0;6) ,B(5;-3) ,C(-2;3) Tìm D đ t giác ABCD làể ứ
hình bình hành
II.PH N DÀNH CHO THÍ SINH T NG BANẦ Ừ
A. Thí sinh ban c b nơ ả
Bài1:(2đ)a/Gi i và bi n lu n ph ng trình sau theo tham s m: mả ệ ậ ươ ố 2 x –
m2 – 4m = 4x + 4
b/ Ch ng minh b t đ ng th c sau ? (a + b)( b + c)( c + a)ứ ấ ẳ ứ
≥
8abc . v i a,b,c ớ> 0
Bài2:(1đ) Cho sinx =
4
3
và 900 < x < 1800. Tính giá tr c a bi u th c: P =ị ủ ể ứ
7
( cosx + tanx ) B.Thí sinh ban KHTN
Bài 1.( 1đ) Tìm giá tr nh nh t c a hàm sị ỏ ấ ủ ố
x
xxf 8
12)( ++=
, v i m iớ ọ
(0, ).x
∈ +∞
Bài 2. ( 2đ )
a) Cho 4 đi m ểA, B, C, D. Ch ng minh r ng ứ ằ
0... =++ ABDCCADBBCDA
T đó suy ra tính ch t đ ng quy c a ba đ ng cao trong m t tamừ ấ ồ ủ ườ ộ
giác.
b) Ch ng minh r ng ứ ằ
6 6 2 2
sin os 1 3sin cosx c x x x
+ = −
.
------------------------------
Đ 3:ề
Câu 1: (2 đi m)ể

a. Gi i ph ng trình: ả ươ
10239 =−+ xx
b. Xác đ nh m đ ph ng trình sau có 2 nghi m phân bi t cùng d u: ị ể ươ ệ ệ ấ
(m-1)x2 +2(m+2)x + m - 1 = 0.
Câu 2: (2 đi m)ể
a. Ch ng minh đ th c a hàm s : ứ ồ ị ủ ố
xxy −−+= 22
có tâm đ i x ng làố ứ
g c to đ .ố ạ ộ
b. L p b ng bi n thiên và v đ th c a hàm s : y = -xậ ả ế ẽ ồ ị ủ ố 2 - 3x +2
Câu 3: (2đ đi m)ể
a. Gi i h ph ng trình: ả ệ ươ
=++
=++
2
4
22
yxyx
yxyx
b. Cho a, b, c
≥
0 và a + b + c = 1.
Ch ng minh r ng (1 - a)(1 - b)(1 - c) ứ ằ
≥
8abc
Câu 4:(1đ) Cho tam giác ABC. Xác đ nh đi m M sao choị ể
( )
2MA MB BA BC+ = −
uuur uuur uuur uuur
Câu 5: (3đ)
Trong m t ph ng Oxy cho 3 đi m A(2;5)B(-1;3), C(3;1) ặ ẳ ể
a/ Xác đ nh đi m D sao cho ị ể
AB AC AD+ =
uuur uuur uuur
b/ Xác đ nh t a đ giao đi m c a OA và BC.ị ọ ộ ể ủ
----------------------------------------
Đ 4:ề
Câu 1(2 điêm)a.Gi i ph ng trình ả ươ
3 -2x 1 -2x =
b.Cho ph ng trình xươ 2 - 2 (m + 1)x + m2 - 2m + 1 = 0.
Xác đ nh m đ ph ng trình có hai nghi m phân bi t xị ể ươ ệ ệ 1, x2 th a xỏ1 + x2 =
2x1x2
Câu 2 (3 điêm)a.Xét tính ch n, l c a hàm s y = ẵ ẻ ủ ố
3 -x 3 x ++
b.Lâp bang biên thiên va ve đô thi ham sô ! " # $ # # " y = 2x2 - 3x –
5
c.Xac đinh ham sô bâc hai biêt đô thi cua no la môt" # " " # ! " #
đ ng Parabol co đinh ươ# " !
1 3
( ; )
2 4
I−
va đi qua điêm A(1;-1).# !
Câu 3 (1 điêm ) Cho a, b, c là ba c nh c a m t tam giác. Ch ng minh r ng:ạ ủ ộ ứ ằ
(a + b) (b + c) (c + a) ≥ 8abc
Câu 4 (3,5 điêm) Cho tam giác ABC v i A(1;0), B(2;6), C(7; -8)ớ
a) Tìm t a đ vect ọ ộ ơ
3 2u AB AC BC= + −
r uuur uuur uuur
b) Tìm t a đ đi m D sao cho ọ ộ ể ∆BCD có tr ng tâm là đi m Aọ ể
c) Tim toa đô điêm E sao cho ABCE la hinh binh hanh .# ! # # # #
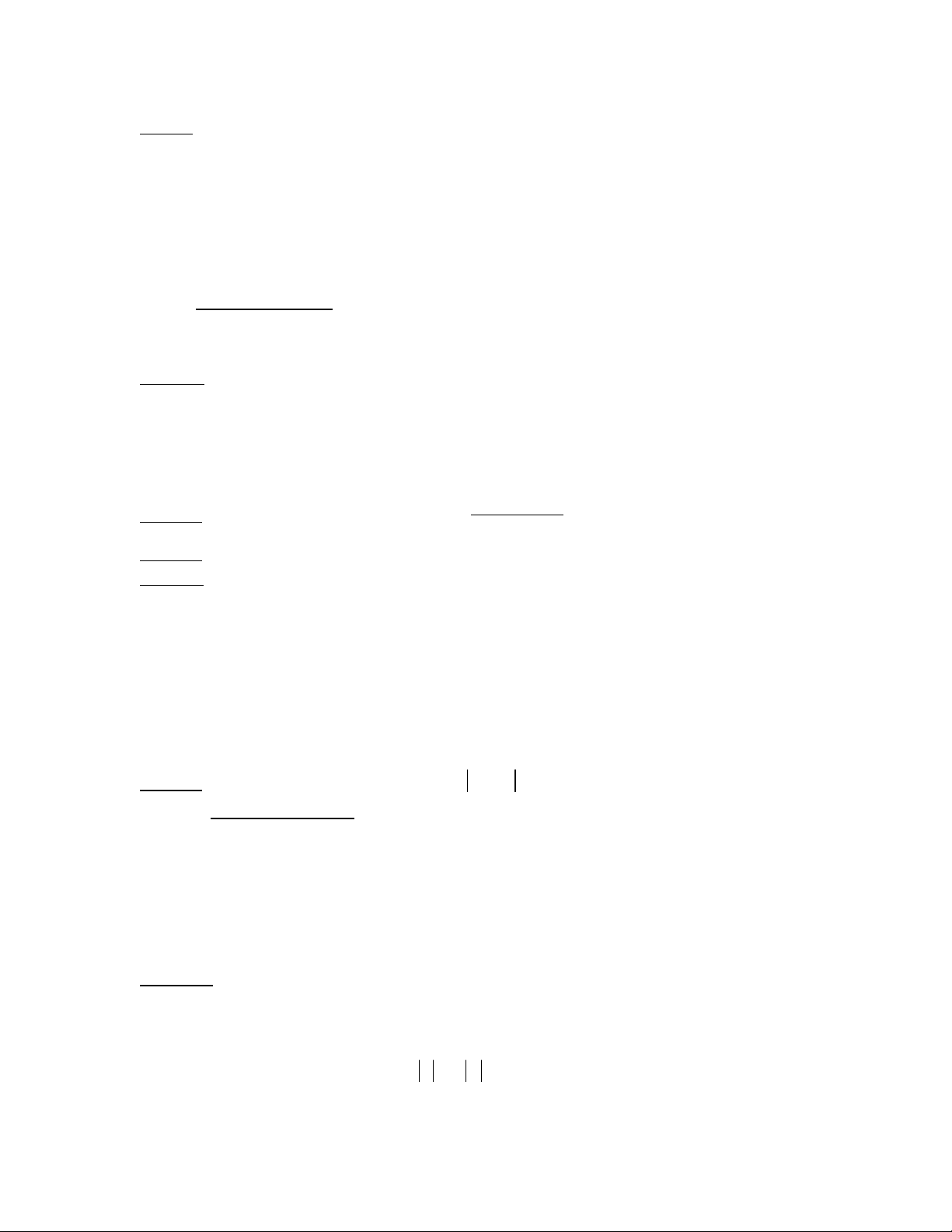
Câu 5(0,5 điêm) S d ng máy tính đ tính cos 138ử ụ ể 016’41”
(Ghi qui trinh bâm may, k t qu làm tròn v i 4 ch s th p phân / ghi chu ế ả ớ ữ ố ậ
loai may tinh đang s dung) ư
------------------------------------------------------------------------------
Đ 5:ề
I. Ph n chungầ: (H c sinh h c c hai ch ng trình c b n và nângọ ọ ả ươ ơ ả
cao đ u ph i làm nh ng câu c a ph n này)ề ả ữ ủ ầ
Câu 1: (1,25đ) Cho m nh đ P: “S th c d ng c ng v i 9 l n ngh chệ ề ố ự ươ ộ ớ ầ ị
đ o c a nó luôn l n h n ho c b ng 6 ”. ả ủ ớ ơ ặ ằ
a) Dùng ký hi u ệ
∃
ho cặ
∀
đ vi t m nh đ P. L p m nh đ ph đ nhể ế ệ ề ậ ệ ề ủ ị
c a m nh đ P.ủ ệ ề
b) Ch ng minh m nh đ P đúng.ứ ệ ề
Câu 2: (1đ) Ch ng minh hàm s ứ ố
4 2
2 3x x
yx
+ +
=
là hàm s l .ố ẻ
Câu 3: (1,5đ) L p b ng bi n thiên và v Parabol (P): y = xậ ả ế ẽ 2 + 4 x + 3.
Câu 4: (2,75đ) Trong m t ph ng t a đ Oxy cho tam giác ABC v i A(1;-ặ ẳ ọ ộ ớ
2), B(3;-5), C(2;-1).
a) Xác đ nh t a đ tr ng tâm G c a tam giác ABC.ị ọ ộ ọ ủ
b) Tính g n đúng đ l n góc A c a tam giác ABC theo đ phút giâyầ ộ ớ ủ ộ
(làm tròn đ n s nguyên giây).ế ố
c) Xác đ nh t a đ đi m D sao cho t giác ACDB là hình bình hành.ị ọ ộ ể ứ
d) Ch ng minh r ng, v i m i đi m M ta luôn có :ứ ằ ớ ọ ể
5 6 5MA MB MC CA CB+ − = +
uuur uuuur uuuur uuur uuur
.
Câu 5: (0, 75đ) Gi i ph ng trình: ả ươ
2 1 1x x− = +
.
II. Ph n riêng:ầ (H c sinh h c ch ng trình nào thì ch làm trongọ ọ ươ ỉ
ph n đã ch ra d i đây; n u làm c hai ph n thì s không đ c ch m cầ ỉ ướ ế ả ầ ẽ ượ ấ ả
hai ph n này)ầ
a) Dành cho h c sinh h c ch ng trình nâng cao:ọ ọ ươ
Câu 6a: (1,75 đ) Cho h ph ng trình (I):ệ ươ
2 3 1
2 2
mx y m
x my
+ = −
+ =
a) Gi i và bi n lu n h ph ng trình (I) theo m. ả ệ ậ ệ ươ
b) Khi (x; y) là nghi m duy nh t c a h ph ng trình (I). Hãy tìm giáệ ấ ủ ệ ươ
tr nh nh t c a bi u th c ị ỏ ấ ủ ể ứ
2A x y= +
.

Câu7a: (1,0đ) Cho tam giác ABC có ba góc đ u nh n. Ch ng minh r ng :ề ọ ứ ằ
cot cot c
A B hc
+ =
.T đó suy ra ừ
2 2 2
( )
cot cot cot R a b c
A B C abc
+ +
+ + =
.(R là bán
kính đ ng tròn ngo i ti p tam giác ABC; BC = a, AC = b, AB = c; hườ ạ ế c là
đ dài đ ng cao c a tam giác ABC xu t phát t đ nh C)ộ ườ ủ ấ ừ ỉ
b) Dành cho h c sinh h c ch ng trình c b n:ọ ọ ươ ơ ả
Câu 6b: (1,0đ) Gi i và bi n lu n ph ng trình sau theo tham s m: mx +ả ệ ậ ươ ố
m = x + m2.
Câu 7b : (0,75đ) Cho
tan 3
α
= −
. Hãy tính giá tr c a bi u th cị ủ ể ứ
2sin cos
sin 4cos
P
α α
α α
−
=+
.
Câu 8b: (1đ) Cho ph ng trình xươ 2 - 3mx + m = 0, v i m là tham s . Tìm mớ ố
đ ph ng trình có hai nghi m xể ươ ệ 1, x2 khác không và x1 = 2x2.
…….………….. H t …………………ế
Đ 6:ề
Bài 1: ( 1 đi m) Tìm t p xác đ nh c a hàm s : ể ậ ị ủ ố
2
x
y 3x 6 x 4
= - + -
Bài 2: ( 2.5 đi m ) ể
a) Gi i ph ng trình: ả ươ
- = +2x 3 x 2
b) Tìm m đ ph ng trình: ể ươ
- = -
2
m x 2 4x m
nghi m đúng v i m i sệ ớ ọ ố
th c x.ự
Bài 3: ( 2.5 đi m )ể
a) Tìm Parabol
= - +
2
y x bx c
, bi t r ng: Parabol đó đi qua đi m ế ằ ể
A(1; -1) và B(2; 3).
b) Kh o sát s bi n thiên và v đ th hàm s v a tìm đ c câu a).ả ự ế ẽ ồ ị ố ừ ượ ở
Bài 4: ( 1 đi m ) Cho hình bình hành ABCD có O là giao đi m hai chéo.ể ể
Ch ng minh: ứ
+ + =
uuur uuur uuur uuur
AB AC AD 4AO
Bài 5: ( 3 đi m ) Trong m t ph ng to đ Oxy, cho các đi m A(-1;2),ể ặ ẳ ạ ộ ể
B(2;3), C(5;1).


























