intTypePromotion=1
zunia.vn Tuyển sinh 2024 dành cho Gen-Z zunia.vn zunia.vn
ADSENSE
 » 
 » 

ĐỀ TÀI: THIẾT KẾ BỘ LỌC FIR THÔNG CAO BẰNG PHƯƠNG PHÁP LẤY MẪU TẦN SỐ

Chia sẻ: Ta Duoc | Ngày: | Loại File: PDF | Số trang:22

Thêm vào BST
Báo xấu
494
lượt xem 80
download
 
  Download Vui lòng tải xuống để xem tài liệu đầy đủ

Với xu hướng số hóa các hệ thống thông tin hiện nay,việc xử lý tín hiệu số ngày càng trở nên quan trọng với khả năng xử lý thông tin một các ưu việt. Để có thể tiếp cận được lĩnh vực này, chúng ta cần có những kiến thức cơ bản về tín hiệu số và các phương pháp xử lý. Một trong những kiến thức quan trọng đó là thiết kế bộ lọc số - hệ thống có thể làm thay đổi tín hiệu để phù hợp với mục đích của con người...

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: ĐỀ TÀI: THIẾT KẾ BỘ LỌC FIR THÔNG CAO BẰNG PHƯƠNG PHÁP LẤY MẪU TẦN SỐ

  1. ĐẠI HỌC QUY NHƠN --- oOo --- BÀI TẬP LỚN MÔN HỌC: XỬ LÝ SỐ TÍN HIỆU ĐỀ TÀI: THIẾT KẾ BỘ LỌC FIR THÔNG CAO BẰNG PHƯƠNG PHÁP LẤY MẪU TẦN SỐ Người hướng dẫn : Sinh viên thực hiện : Lớp : Quy Nhơn , tháng 5/2011
  2. Thiết kế lọc FIR thông cao bằng phương pháp lấy mẫu tần số Trang 2 LỜI NÓI ĐẦU Với xu hướng số hóa các hệ thống thông tin hiện nay,việc xử lý tín hiệu số ngày càng trở nên quan trọng với khả năng xử lý thông tin một các ưu việt. Để có thể tiếp cận được lĩnh vực này, chúng ta cần có những kiến thức cơ bản về tín hiệu số và các phương pháp xử lý. Một trong những kiến thức quan trọng đó là thiết kế bộ lọc số - h ệ thống có thể làm thay đổi tín hiệu để phù hợp với mục đích của con người. Trong xử lý số tín hiệu, tồn tại nhiều bộ lọc số khác nhau như: bộ lọc thông thấp, bộ lọc thông dải, bộ lọc vi phân,… Để thiết kế các bộ lọc thích hợp, trước hết phải xác định yêu cầu thực tế dựa trên các chỉ tiêu kỹ thuật cho trước, trên cơ sở đó định hình cấu trúc bộ lọc và phương pháp thiết kế tối ưu. Cấu trúc bộ lọc có thể là: cấu trúc FIR (bộ lọc số có đáp ứng xung chiều dài xác định) hoặc cấu trúc IIR (bộ lọc số có đáp ứng xung chiều dài không xác định). Ph ương pháp thiết kế có thể là: phương pháp cửa sổ, phương pháp lấy mẫu tần số, hoặc phương pháp xấp xỉ tối ưu,… Được sự phân công của thầy giáo , trên cơ sở những kiến thức đã học, tôi đã tìm hiểu bộ lọc FIR theo phương pháp lấy mẫu tần số. Tôi xin chân thành cám ơn thầy giáo , bạn bè cùng lớp đã tận tình hướng dẫn để tôi có thể hoàn thành đề tài này. Chắc chắn đề tài sẽ không tránh khỏi những thiếu sót rất mong được sự góp ý của quý thầy cô và các bạn. Xin chân thành cảm ơn! Quy nhơn, tháng 5 n ăm 2011 Người thực hiện
  3. Thiết kế lọc FIR thông cao bằng phương pháp lấy mẫu tần số Trang 3 MỤC LỤC LỜI NÓI ĐẦU ............................................................................................................. 2 MỤC LỤC ................................................................................................................... 3 Phần 1. CƠ SỞ LÝ THUYẾT ................................ ...................................................... 4 1.1. Dẫn nhập ................................................................................................ ........... 4 1.2. Cấu trúc của bộ lọc FIR..................................................................................... 6 a. Cấu trúc dạng trực tiếp ..................................................................................... 6 b . Cấu trúc dạng ghép tầng: .................................................................................. 7 c. Cấu trúc dạng pha tuyến tính: ................................................................ ........... 7 1.3. Các đặc tính của bộ lọc FIR pha tuyến tính ................................ ....................... 8 a. Đáp ứng xung h(n): .......................................................................................... 9 b . Đáp ứng tần số H(ej):................................ .................................................... 11 1.4 Phương pháp thiết kế lấy m ẫu tần số : .............................................................. 14 a. Phương pháp thiết kế đơn giản ....................................................................... 15 b . Phương pháp thiết kế tối ưu ............................................................................ 15 Phần 2. THIẾT KẾ LỌC FIR THÔNG CAO ............................................................. 16 2.1. Bài toán thiết kế .............................................................................................. 16 2.2. Phương pháp thiết kế....................................................................................... 16 2.3. Thu ật toán và chương trình Matlab................................ ................................ .. 17 a. Lưu đồ thu ật toán: .......................................................................................... 17 b ) Chương trình................................................................ ................................ .. 19 c) Kết quả .......................................................................................................... 21 TÀI LIỆU THAM KHẢO .......................................................................................... 22
  4. Thiết kế lọc FIR thông cao bằng phương pháp lấy mẫu tần số Trang 4 Phần 1. CƠ SỞ LÝ THUYẾT 1.1. Dẫn nhập Việc thiết kế mộ t bộ lọc số tiến hành theo 3 bước:  Đưa ra các chỉ tiêu: Trước khi thiết kế một bộ lọc chúng ta cần xác định các chỉ tiêu. Các chỉ tiêu được xác đ ịnh bởi các ứng dụng cụ thể khác nhau.  Tìm các xấp xỉ: Một khi chỉ tiêu đã được xác đ ịnh, ta sử dụng các khái niệm và công cụ toán học khác nhau để tiến tới biểu diễn và tính gần đúng cho bộ lọ c với tập các ch ỉ tiêu đ ã cho. Và đây là chủ đ ề chính của việc thiết kế lọc số .  Thực hiện bộ lọ c: Kết qu ả của các bước trên cho mô tả dưới dạng một phương trình sai phân, hoặc một hàm hệ thống H(z), hoặc mộ t đáp ứng xung h(n). Từ các mô tả này chúng ta có th ể thi hành bộ lọ c b ằng ph ần cứng hoặc phần mềm mô phỏng trên máy tính. Trong những p hần tiếp sau đây, để mô tả các chỉ tiêu của bộ lọc chúng ta sẽ xem xét việc thiết kế một bộ lọc thông thấp như một ví dụ cơ sở. Có 2 nhóm chỉ tiêu: Các chỉ tiêu tuyệt đối (Absolute Specifications) và các chỉ tiêu tương đối (Relative Specifications - DB). 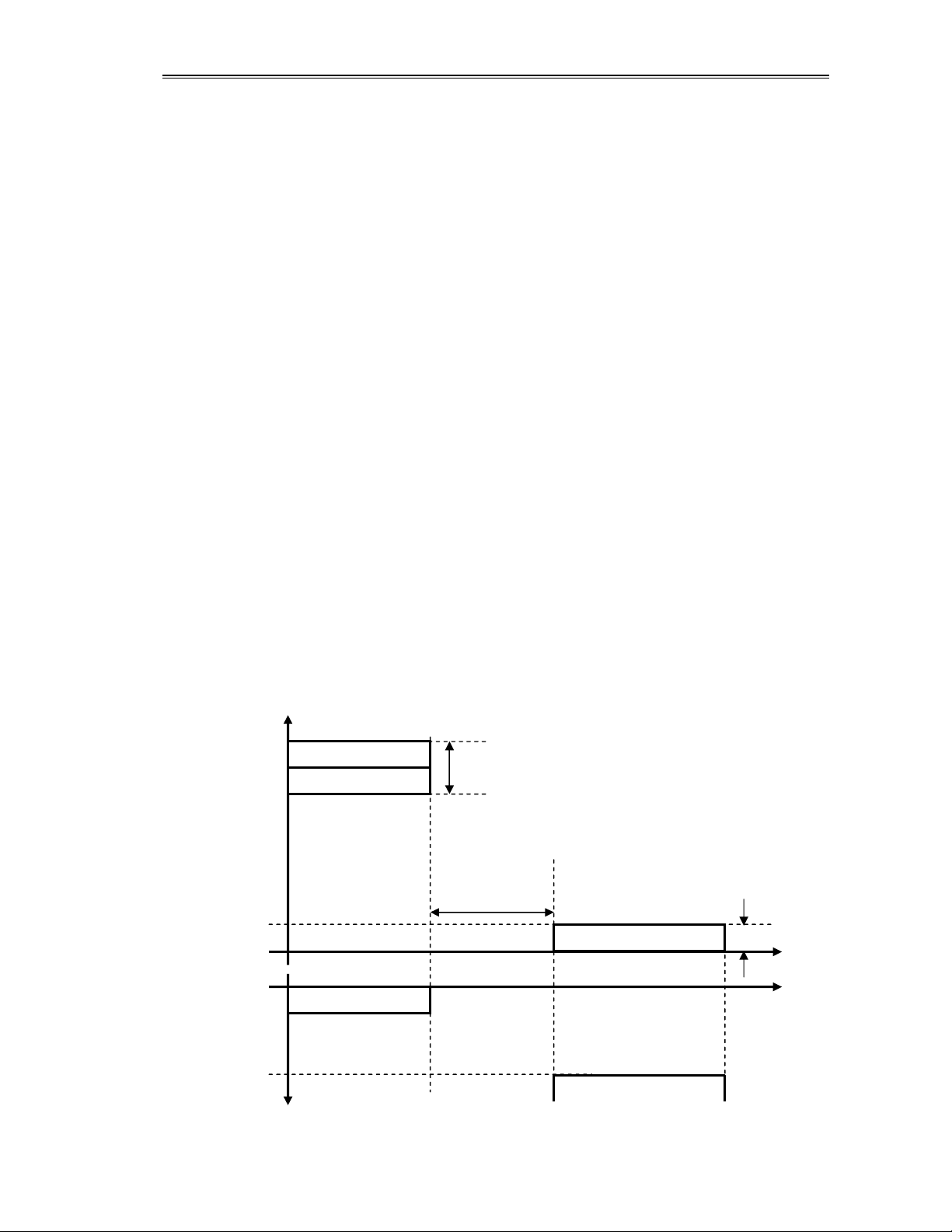Trên hình 1.1 là mô tả các chỉ tiêu của bộ lọc FIR thông thấp (Low Pass Filter): |H(ejw)| 1+1 Độ gợn dải thông 1 1 -1 Độ gợn dải chắn Dải chuyển tiếp 2 ws  wp 0 0 Rp As Decibels Hình 1.1 Các chỉ tiêu của bộ lọc FIR: các chỉ tiêu tuyệt đối và tương đối
  5. Thiết kế lọc FIR thông cao bằng phương pháp lấy mẫu tần số Trang 5 Trong đó:  Band [0, wp] được gọi là dải thông, và 1 là dung sai (gợn sóng) đ ược chấp nhận trong đáp ứng dải thông lý tưởng.  Band [ws,  ] được gọi là dải chắ n, và 2 là dung sai ở dải ch ắn.  Band [wp , ws] được gọi là dả i chuyển tiếp, và không có ràng buộc nào về đáp ứng biên độ trong d ải này Các chỉ tiêu tương đối gồm có:  Rp: Độ gợn sóng trong d ải thông tính theo dB.  As : Suy hao trong dải chắn tính theo dB. Quan h ệ giữa các chỉ tiêu n ày như sau: 1 1 R p  20 log10  0 (0) (1.1) 1  1 2  0 (>>1) (1.2) A s  20 log10 1  1 Các chỉ tiêu trên được đưa ra đối với bộ lọc FIR thông thấp, và tất nhiên đối với các bộ lọc khác như thông cao HPF (High Pass Filter), thông d ải BPF (Band Pass Filter) đều có thể được định nghĩa tương tự. Tuy nhiên, các tham số thiết kế quan trọng nh ất là các dung sai dải tần và các tần số cạnh-dải (tolerance or ripples and band -edge frequencies). Bởi vậy, trong phần 1 về cơ sở lý thuyết này chúng ta ch ỉ tập trung vào bộ lọc FIR thông thấp. Việc thiết kế cụ thể cho bộ lọc FIR thông dải bằng k ỹ thuật cửa sổ sẽ được phát triển trên cơ sở lọ c thông th ấp và sẽ được mô tả chi tiết trong phần 2. Việc thiết kế và thự c hiện lọc FIR có những thuận lợi sau đây:  Đáp ứng pha là tuyến tính.  Dễ thiết kế do không gặp các vấn đề ổn định (lọ c FIR luôn ổn định).  Việc th ực hiện rất hiệu quả.  Có thể sử dụng DFT để thự c hiện Đáp ứng pha là tuyến tính (linear phase response) mang lại những thuận lợi sau:  Bài toán th iết kế chỉ gồm các phép tính số học thực chứ không cần phép tính số học phức.  Bộ lọc pha tuyến tính không có méo trễ nhóm và chỉ bị trễ mộ t khoảng không đổi.
  6. Thiết kế lọc FIR thông cao bằng phương pháp lấy mẫu tần số Trang 6  Đối với bộ lọc có chiều dài M (hoặc bậc M-1) số phép toán có b ậc M/2 như đ ã khảo sát trong th ực hiện bộ lọc có pha tuyến tính. 1.2. Cấu trúc của bộ lọc FIR Một bộ lọc đáp ứng xung hữu hạn với h àm hệ thống có dạng: M 1 H( z)  b 0  b1 z 1    b M 1 z1M   b n z n (1.3) n 0 Như vậy đáp ứng xung h(n) là: bn 0  n  M  1 h( n)   (1.4) 0 else Và phương trình sai phân là: y(n )  b 0 x ( n)  b1 x (n  1)    b M1 x (n  M  1) (1.5) Đây chính là tích chập tuyến tính của các dãy hữu hạn. Bậc của bộ lọc là M-1, trong khi chiều d ài của bộ lọc là M (bằng với số lượng các hệ số). Các cấu trúc bộ lọc FIR luôn luôn ổn định, và tương đối đơn giản hơn so với các cấu trúc bộ lọc IIR. Hơn th ế nữa, các bộ lọc FIR có thể được thiết kế để có một đáp ứng pha tuyến tính và đó là điều cần thiết trong một số ứng dụng. Chúng ta sẽ xem xét lần lượt các cấu trúc của bộ lọc FIR sau đây: a. Cấu trúc dạng trực tiếp Phương trình sai phân đ ược thực hiện bởi một dãy liên tiếp các bộ trễ do không có đường phản hồi: (1.6) y(n )  b 0 x ( n )  b1 x (n  1)    b M 1 x (n  M  1) Do m ẫu thức bằng đ ơn vị nên ta chỉ có một cấu trúc dạng trực tiếp duy nhất. Cấu trúc dạng trực tiếp được cho trong hình 1.2 với M = 5: x(n) z-1 z-1 z-1 z-1 b1 b2 b3 b4 b0 y(n) Hình 1.2 Cấu trúc lọc FIR dạng trực tiếp
  7. Thiết kế lọc FIR thông cao bằng phương pháp lấy mẫu tần số Trang 7 b. Cấu trúc dạng ghép tầng: Hàm hệ thống H(z) được biến đổi thành các tích của các khâu bậc 2 với các hệ số thực. Các khâu này được thực hiện ở dạng trực tiếp và bộ lọc tổng thể có dạng ghép tầng của các khâu bậc 2. b b  H( z)  b 0  b1 z 1    b M 1z1M  b 0 1  1 z 1    M 1 z1 M   b0 b0  K  b 0  (1  B k ,1z 1  B k , 2 z 2 ) (1.7) k 1 M  trong đó K    , Bk,1 và Bk,2 là các số thực đại diện cho các hệ số của các khâu bậc 2 2. Cấu trúc dạng ghép tầng được cho trong hình 1.3 với M = 7: b0 y(n) x(n) z-1 B z-1 B z-1 B 2,1 3,1 1,1 z-1 B z-1 B z-1 B 3,2 1,2 2,2 Hình 1.3 Cấu trúc lọc FIR dạng ghép tầng c. Cấu trúc dạng pha tuyến tính: Đối với các bộ lọc chọn tần, người ta mong muốn có đáp ứng pha là hàm tuyến tính theo tần số, nghĩa là: H(e j )           (1.8)  trong đó   0 hoặc  và  là một hằng số. 2 Đối với bộ lọc FIR nhân quả có đáp ứng xung trong khoảng [0, M-1], thì các điều kiện tuyến tính là: h (n )  h( M  1  n );   0, 0  n  M  1 (1.9) h (n )   h (M  1  n );     / 2, 0  n  M  1 (1.10) Xét phương trình sai phân được cho trong phương trình (1.5) với đáp ứng xung đối xứng trong phương trình (1.9), ta có: y(n )  b 0 x ( n )  b1 x ( n  1)    b1 x ( n  M  2)  b 0 x( n  M  1)  b 0 [ x (n )  x (n  M  1)]  b1 [ x (n  1)  x( n  M  2)]  
  8. Thiết kế lọc FIR thông cao bằng phương pháp lấy mẫu tần số Trang 8 Sơ đồ khối thực hiện phương trình sai phân trên được mô tả trong hình 1.4 dưới đây đối với cả M lẻ và M ch ẵn: Đối với M lẻ: M = 7, còn đối với M chẵn: M = 6 z-1 z-1 x(n) z-1 M=7 z-1 -1 -1 z z b3 b0 b1 b2 y(n) z-1 z-1 x(n) z-1 M=6 -1 -1 z z b0 b1 b2 y(n) Hình 1.4 Cấu trúc lọc FIR pha tuyến tính với các hệ số M chẵn và lẻ Rõ ràng, với cùng một bậc của bộ lọc (cùng M) cấu trúc pha tuyến tính sẽ tiết kiệm được 50% các bộ nhân so với cấu trúc dạng trực tiếp. 1.3. Các đặc tính của bộ lọc FIR pha tuyến tính Trong p hần này chúng ta sẽ thảo luận về h ình dạng của đáp ứng xung, đáp ứng tần số trong h àm hệ thống của các bộ lọc FIR pha tuyến tính. Cho h(n), trong đó 0  n  M – 1, là đáp ứng xung có chiều dài M thì hàm truyền hệ thống là: M 1 M 1 H( z)   h ( n )z  n  z ( M 1)  h (n )z M 1n (1.11) n 0 n 0 có (M-1) điểm cực ở gốc (trivial poles) và M-1 điểm không nằm ở vị trí bất kỳ trên mặt phẳng z. Đáp ứng tần số là: M 1 H ( e j  )   h ( n )e  j  n ,       (1.12) n 0
  9. Thiết kế lọc FIR thông cao bằng phương pháp lấy mẫu tần số Trang 9 a. Đáp ứng xung h(n): Chúng ta có thể đưa ra ràng buộc pha tuyến tính: H(e j )  ,       (1.13) trong đó:  là một hằng số trễ pha. Ta đã biết rằng h(n) phải đối xứng, nghĩa là: M 1 h (n )  h ( M  1  n ), 0  n  M  1,   (1.14) 2 Do đó h(n) là đối xứng theo , là chỉ số đối xứng. Có hai kiểu đối xứng: M 1  M lẻ: Trong trường hợp này,   là m ột số nguyên. Đáp ứng xung 2 được mô tả trong hình 1.5 dưới đây: Hình 1.5 Đáp ứng xung đối xứng, M lẻ M 1  M ch ẵn: Trong trường hợp n ày,   không phải là một số nguyên. Đáp 2 ứng xung đư ợc mô tả bằng hình 1.6 dưới đây: Hình 1.6 Đáp ứng xung đối xứng, M chẵn
  10. Thiết kế lọc FIR thông cao bằng phương pháp lấy mẫu tần số Trang 10 Ta cũng có bộ lọc FIR pha tuyến tính loại hai nếu ta yêu cầu đáp ứng pha H e j  tho ả m ãn điều kiện: H(e j )     với       (1.15) Đáp ứng pha là đường thẳng nhưng không đi qua gốc. Trong trường hợp n ày  không ph ải là h ằng số trễ pha, nhưng: dH(e j )   (1.16) d là hằng số, chính là trễ nhóm ( là m ột hằng số trễ nhóm). Trong trường hợp này, các tần số được làm trễ với một tốc độ không đổi. Nhưng một số tần số có thể được làm trễ với tốc độ lớn hơn ho ặc nhỏ h ơn. Đối với kiểu pha tuyến tính này, có thể thấy rằng: M 1  h (n )  h (M  1  n ), 0  n  M  1 và   ,  (1.17) 2 2 Điều này có nghĩa rằng đáp ứng xung h(n) là phản đối xứng (antisymmetric). Chỉ M 1 số đối xứng vẫn là   . Một lần nữa chúng ta lại có 2 kiểu, cho M lẻ và M chẵn. 2 M 1  M lẻ: Trong trường hợp này,   là m ột số nguyên. Đáp ứng xung 2 được mô tả bằng hình 1.7 dưới đây: Hình 1.7 Đáp ứng xung phản đối xứng, M lẻ M 1  M 1 Lưu ý rằng mẫu h() tại   phải bằng 0, nghĩa là, h    0. 2 2
  11. Thiết kế lọc FIR thông cao bằng phương pháp lấy mẫu tần số Trang 11 M 1  M ch ẵn: Trong trường hợp n ày,   không phải là một số nguyên. Đáp 2 ứng xung đư ợc mô tả trong hình 1.8 . Hình 1.8 Đáp ứng xung phản đối xứng, M chẵn b. Đáp ứng tần số H(ej): Khi tổ hợp hai loại đối xứng và phản đối xứng với M chẵn và M lẻ, ta có bốn kiểu lọc FIR pha tuyến tính. Đáp ứng tần số của mỗi kiểu có biểu thức và hình dạng riêng. Để nghiên cứu các đáp ứng pha của các kiểu này, ta viết biểu thức của H(ej) như sau:  M 1 H(e j )  H r (e j )e j() ;    ,   (1.18) 2 2 trong đó Hr(ej) là hàm đáp ứng độ lớn chứ không phải là hàm đáp ứng biên độ. Đáp ứng độ lớn là một hàm thực, có thể vừa dương vừa âm, không giống đáp ứng biên độ luôn luôn dương. Đáp ứng pha kết hợp với đáp ứng biên độ là một h àm không liên tục, trong khi kết hợp với đáp ứng độ lớn là một hàm tu yến tính liên tục.  Bộ lọc FIR pha tuyến tính Loại-1 (Type 1): Đáp ứng xung đối xứng, M lẻ M 1 là một biến nguyên, và h n   h M  1  n  , Trong trường hợp n ày   0 ,   2 0  n  M  1 , thì ta có th ể chứng tỏ rằng: M 1  / 2 H(e j )    a n  cos n e  j M 1 / 2 (1.19)  n 0    trong đó:
  12. Thiết kế lọc FIR thông cao bằng phương pháp lấy mẫu tần số Trang 12  M 1 a 0   h  với mẫu ở chính giữa (1.20)  2 M 3  M 1  a n   2h  với 1  n   n 2 2   Bộ lọc FIR pha tuyến tính Loại-2 (Type 2): Đáp ứng xung đối xứng, M chẵn M 1 Trong trường hợp n ày   0 , h n   h M  1  n  , 0  n  M  1 , nhưng   2 không ph ải là m ột biến nguyên, thì ta có thể chứng tỏ rằng: M / 2 1   H(e j )    bn cos n   e  jM 1 / 2 (1 .21) 2    n 1 trong đó: M M  bn   2h   n  với n  1,2,..., (1.22) 2 2  So sánh (1.21) và (1.18), ta có:  1  M/2 H r ()   bn cos n   (1.23) 2   n 1  1  M/2 Lưu ý: Tại    , ta có H r ()   bn cos n    0 m à không cần quan tâm 2   n 1 đến b(n) hoặc h(n). Do đó chúng ta không thể sử dụng loại này (h(n) đối xứng, M ch ẵn) đối với bộ lọc thông cao hoặc bộ lọc chắn dải.  Lọc FIR pha tuyến tính Loại-3 (Type 3): Đáp ứng xung phản đối xứng, M lẻ  M 1   Trong trường hợp n ày ta có một biến nguyên, , là 2 2  M 1 h n   h M  1  n  , 0  n  M  1 , và h    0 thì ta có thể chứng tỏ: 2    M 1   M 1  / 2 j     H(e )    cn sin n  e  2  2 j (1.24)  n 0    trong đó M  M 1  cn   2h  với n  1,2,..., (1.25)  n 2 2 
  13. Thiết kế lọc FIR thông cao bằng phương pháp lấy mẫu tần số Trang 13 So sánh (1.24) và (1.18), ta có: M 1  / 2 H r    cn sin n (1.26) n 0 Lưu ý: Tại   0 và    , ta có H r   0 mà không cần quan tâm c(n) hoặc h(n).  j  j , điều đó có nghĩa là jH r  là thuần ảo. Do đó, loại bộ lọc này Hơn thế nữa, e 2 không thích hợp đối với việc thiết kế bộ lọc thông thấp hoặc thông cao. Tuy nhiên, điều này thích hợp đối với việc xấp xỉ các bộ vi phân và bộ biến đổi Hilbert số lý tưởng.  Lọc FIR pha tuyến tính Loại-4(Type 4 ):Đáp ứng xung phản đối xứng, M chẵn  M 1 , h n   h M  1  n  , 0  n  M  1 , nhưng   Trong trường hợp n ày   2 2 không ph ải là m ột biến nguyên, thì ta có thể chứng tỏ rằng:  M 1    M / 2 1   j  2     H(e )    dn sin  n  e 2 j  (1.27) 2     n 1 trong đó: M M  d n   2h   n  với n  1,2,..., (1.28) 2 2  So sánh (1.27) và (1.18), ta có:  1  M/2 H r ()   d n sin  n   (1.29) 2   n 1  j Lưu ý: Tại    , H r (0)  0 và e  j . Do vậy, loại n ày cũng thích hợp cho việc 2 thiết kế các bộ vi phân số và bộ biến đổi Hilbert số. Bảng sau đây mô tả khả năng thích hợp trong việc thiết kế các bộ lọc và các bộ biến đổi Hilbert số, bộ vi phân số của 4 loại lọc FIR pha tuyến tính đã nêu: Type LPF HPF BPF SBF Hilbert Differentiator     FIR Type 1   FIR Type 2    FIR Type 3     FIR Type 4
  14. Thiết kế lọc FIR thông cao bằng phương pháp lấy mẫu tần số Trang 14 1.4 Phương pháp thiết kế lấ y mẫ u tần số : Theo phương pháp lấy m ẫu tần số , đáp ứng tần số yêu cầu Hd(ejw) trước tiên đư ợc lấy mẫu đều ở M điểm cách đều nhau giữa 0 và 2pi : H(k)= Hd(ej2k/M) k=0,1,........M-1 Các m ẫu tần số n ày tạo thành DFT M điểm mà biến đổi ngh ịch là bộ lọc FIR có bậc M 1 1 j 2  nk / M  H ( k )e M-1: h( n )  0  n  M 1 M k 0 Đáp ứng thực tế là nội suy của các mẫu được cho bởi: 1  z M M 1 M 1 H (k ) H ( z )   h( n) z  n  1 z 1 e j 2  nk / M M n 0 k 0 Đáp ứng pha đối với kiểu 1 và 2 :   M  1  2k   M  1   2  M , k  0, ,    2   H ( k )     M  1  2 ( M  k ) , k   M  1  1, , M  1    2    2  M    Đáp ứng pha đối với kiểu 3 và 4     M  1  2k   M  1   2    2  M , k  0, ,    2 H (k )             M  1  2 ( M  k ) , k   M  1   1, , M  1     2   2   2  M     Hình 1.9 mô tả kỹ thu ật lấy mẫu tần số : ... ... 1 1 ... ... . . . . . 3. . .4 01 2 4 5 6 7 01 2 3 5 6 7 8 Từ hình trên ta nh ận thấy : Lỗi xấp xỉ là hiệu của đáp ứng lý tưởng và đáp ứng thực tế b ằng không tại các tần số được lấy mẫu.
  15. Thiết kế lọc FIR thông cao bằng phương pháp lấy mẫu tần số Trang 15 Lỗi xấp xỉ ở tất cả các tần số khác phụ thuộc vào hình d ạng của đ áp ứng tần số lý tưởng; ngh ĩa là, đ áp ứng tần số lý tư ởng càng sắc nét thì lỗi xấp xỉ càng lớn. Lỗi càng lớn khi ở gần cạnh dải và càng bé khi ở b ên trong dải. - Có hai cách tiếp cận thiết kế : a. Phương pháp thiết kế đơn giản : sử dụng ý tưởng cơ bản và không đưa ra một ràng buộc nào về lỗi xấp xỉ, nghĩa là chấp nhận lỗi sinh ra do thiết kế. Trong phương pháp này ta đ ặt H(k)= Hd(ej2k/M) k=0,1,........M-1 và sử dụng các công th ức đ ể thu đư ợc đáp ứng xung h(n). Phương pháp này ít được sử dụng trong thực tế. b. Phương pháp thiết kế tố i ưu : cố gắng tối thiểu hóa lỗ i trong dải ch ắn bằng cách thay đ ổi các giá trị củ a m ẫu trong d ải chuyển tiếp. Trong phương pháp này, chúng ta phải tăng M đ ể tạo ra các m ẫu tự do trong d ải chuyển tiếp nghĩa là chúng ta thay đổi các giá trị của chúng để thu được h ệ số suy giảm lớn nhất đố i với M và độ rộng dải chuyển tiếp đã cho. Đây là m ột bài toán tố i ưu hóa và được giải quyết b ằng kỹ thuật quy hoạch tuyến tính. Trong thực tế độ rộng dải chuyển tiếp nói chung khá bé, chỉ chưa được một hoặc hai mẫu. Do đó chúng ta cần tố i ưu hóa tốt nhất hai mẫu để thu được h ệ số suy giảm d ải ch ắn lớn nhất.
  16. Thiết kế lọc FIR thông cao bằng phương pháp lấy mẫu tần số Trang 16 Phần 2. THIẾT KẾ BỘ LỌC FIR THÔNG CAO 2.1. Bài toán thiết kế Hãy thiết kế b ộ lọ c FIR thông cao pha tuyến tính theo phương pháp lấy mẫu tần số, với các chỉ tiêu bộ lọc cần thiết kế được cho như sau:  Cạnh dải ch ắn: ws  Cạnh dải thông: wp  Độ gợn sóng trong dải thông: Rp  Suy hao trong d ải chắn: As Các đ ại lượng này có thể được mô tả trên hình 2.1 như sau: Mag(dB) 0 RP As ws wp F (Hz) Hình 2.1 Các chỉ tiêu của bộ lọc thông cao HPF (high pass filter) Điều kiện: ws< wp
  17. Thiết kế lọc FIR thông cao bằng phương pháp lấy mẫu tần số Trang 17 trong dải chuyển tiếp được thự c hiện lặp đ ể xác đinh được bộ lọc có Rp và As là tốt nhất. Bước 3. Tìm đáp ứng xung của bộ lọc thông cao cần thiết kế Đáp ứng xung của bộ lọc thông cao có thể tìm được bằng phép biển đổi DFT n gược các m ẫu hd(n) : M 1 1 j 2  nk / M  H ( k )e h( n )  0  n  M 1 M k 0 2.3. Thuậ t toán và chương trình Matlab Trong phần này sẽ th ực hiện chương trình thiết kế bộ lọc thông cao bằng phương pháp lấy mẫu tần số. Chương trình sẽ nhận các ch ỉ tiêu yêu cầu của bộ lọc cần thiết kế, sau đó thực hiện các bước thiết kế để tìm được đáp ứng xung h(n). Để khảo sát bộ lọc vừa thiết kế, chương trình cũng sẽ thực hiện tính toán và vẽ đáp ứng biên độ - tần số củ a bộ lọ c theo dB, cũng như vẽ các đáp ứng xung lý tưởng hd(n), hàm cửa sổ w(n) và đáp ứng xung bộ lọc thự c tế h (n). Chương trình được viết và ch ạy trên nền Matlab, với việc sử dụng một số h àm hỗ trợ có sẵn củ a Matlab cho xử lý tín hiệu số, và một số h àm viết thêm được tham khảo từ tài liệu [1] (các hàm dưới dạng các file .m). a. Lưu đồ thuật toán:
  18. Thiết kế lọc FIR thông cao bằng phương pháp lấy mẫu tần số Trang 18 BEGIN Nhập các chỉ tiêu ws, wp As, Rp Chỉ tiêu có No hợp lệ không? Yes Tính số mẫu M Tìm gía trị của T1, T2 tốt nhất ( ứng với Rpd và Asd tốt nhất ) Rpd và Asd có thỏa mãn yêu No cầu không? Yes Tính hd(n) Vẽ hd(n), h(n) và đáp ứng biên độ (dB) của bộ lọc thiết kế. END
  19. Thiết kế lọc FIR thông cao bằng phương pháp lấy mẫu tần số Trang 19 b) Chương trình function [ws wp As Rp]=loc_FIR_thongcao() fprintf('\n'); fprintf('Nhap vao cac thong so cua bo loc thong cao :'); fprintf('\n'); ws1=inpu t('Nhap 0
  20. Thiết kế lọc FIR thông cao bằng phương pháp lấy mẫu tần số Trang 20 MinRp=Rpd; T1op=T1; T2op=T2; end end end Hrs = [zeros(1,N1),T1op,T2op,ones(1,N2-N1-2),T2op,T1op,zeros(1,M-N2 -2)]; Hdr = [0,0,1,1]; wdl = [0,ws,wp,1]; k1 = 0:floor((M-1)/2); k2 = floor((M-1)/2)+1:M-1; angH = [-alpha*(2*pi)/M*k1, alpha*(2*pi)/M*(M-k2)]; H = Hrs.*exp(j*angH); h = real(ifft(H,M)); [db,mag,pha,grd,w] = freqz_m(h,1); [Hr,ww,a,L] = Hr_Type1(h); subplot(1,1,1); subplot(2,2,1);plot(wl(1:alpha+1)/pi,Hrs(1:alpha+1),'o',wdl,Hdr); axis([0,1,-0.1,1.1]); title('Frequency Samples at M=%2.4f',M); xlabel('Frequency in pi units'); ylabel('Hr(k)') set(gca,'XTickMode','manual','XTick',[0;ws;wp;1]) set(gca,'XTickLabelMode','manual','XTickLabels',[0;ws;wp; 1]) set(gca,'YTickMode','manual','YTick',[0,T1op,T2op,1]); grid subplot(2,2,2); stem(l,h); axis([-1,M,-0.4,0.4]) title('Impulse Response'); xlabel('n');ylabel('h(n)');text(M+1,-0.4,'n') subplot(2,2,3); plot(ww/pi,Hr,wl(1:alpha+1)/pi,Hrs(1:alpha+1),'o'); axis([0,1,-0.1,1.1]); title('Amplitude Response') xlabel('Frequency in pi units'); ylabel('Hr(w)') set(gca,'XTickMode','manual','XTick',[0;ws;wp;1]) set(gca,'XTickLabelMode','manual','XTickLabels',[ 0;ws;wp;1]) set(gca,'YTickMode','manual','YTick',[T1op,T2op]); grid subplot(2,2,4);plot(w/pi,db); axis([0,1,-100,10]); grid title('Magnitude Response');xlabel('Frequency in pi units'); ylabel('Decibels'); set(gca,'XTickMode','manual','XTick',[0;ws;wp;1]) set(gca,'XTickLabelMode','manual','XTickLabels',[ 0;ws;wp; 1]) set(gca,'YTickMode','Manual','YTick',[-As;0]); set(gca,'YTickLabelMode','manual','YTickLabels',[As; 0])
ADSENSE

CÓ THỂ BẠN MUỐN DOWNLOAD

LV.26: Bộ 320 Luận Văn Thạc Sĩ Y Học
320 tài liệu
1253 lượt tải
THÔNG TIN
TRỢ GIÚP
HỖ TRỢ KHÁCH HÀNG
Theo dõi chúng tôi

Chịu trách nhiệm nội dung:

Nguyễn Công Hà - Giám đốc Công ty TNHH TÀI LIỆU TRỰC TUYẾN VI NA

LIÊN HỆ

Địa chỉ: P402, 54A Nơ Trang Long, Phường 14, Q.Bình Thạnh, TP.HCM

Hotline: 093 303 0098

Email: support@tailieu.vn

Giấy phép Mạng Xã Hội số: 670/GP-BTTTT cấp ngày 30/11/2015 Copyright © 2022-2032 TaiLieu.VN. All rights reserved.

 

Đồng bộ tài khoản
3=>0