www.vnmath.com
Đ THI CH N H C SINH GI IỀ Ọ Ọ Ỏ
GI I TOÁN TRÊN MÁY TÍNH CASIOẢ
Đ S 4Ề Ố
N u không có yêu c u gì thêm, hãy tính chính xác đ n 4 ch s th p phân.ế ầ ế ữ ố ậ
Bài 1: (3 đi m) ểTính g n đúng các nghi m (đ , phút, giây) c a ph ng trình ầ ệ ộ ủ ươ
3(sin cos ) 5sin cos 2x x x x+ − =
Bài 2: (3 đi m) ểTính g n đúng giá tr c a a và b n u đ ng th ng ầ ị ủ ế ườ ẳ
y ax b= +
đi qua đi m ể
(5;2)A
và là ti pế
tuy n c a Elip ế ủ
2 2
1
16 9
x y
+ =
Bài 3: (3 đi m) ểCho bi t tanx = tan35ế0.tan360.tan370 ….tan520.tan530 và 00 < x < 900
Tính
2 3 2 3
3 3
tan (1 os ) cot (1 sin )
( os sin )(1 osx + sinx)
x c x x x
Mc x x c
+ + +
=+ +
Bài 4: (3 đi m) ểM t s ti n 58000 đ ng đ c g i ti t ki m theo lãi kép. Sau 25 tháng đ c c v n l n l iộ ố ề ồ ượ ử ế ệ ượ ả ố ẫ ạ
là 84155 đ. Tính lãi su t/tháng.ấ
Bài 5: (3 đi m) ểTính g n đúng giá tr l n nh t và nh nh t c a hàm sầ ị ớ ấ ỏ ấ ủ ố
2sin 3cos 1
cos + 2
x x
yx
+ −
=
Bài 6: (3 đi m)ể Cho các hàm s ố
2
2 4
2 3 5 2sin
( ) ; ( )
1 1 cos
x x x
f x g x
x x
+ −
= =
+ +
.
Hãy tính giá tr c a các hàm h p ị ủ ợ
và
t i ạ
35x=
.
Bài 7: (5 đi m) ểCho dãy s ố
n
u
xác đ nh b i: ị ở
( )
1 2 3 1 1 2
1; 2; 3;...; 2 3 3
+ − −
= = = = + +
n n n n
u u u u u u u n
a) Tính giá tr c a ị ủ
4 5 6 7
, , ,u u u u
b) Vi t quy trình b m phím đ tính ế ấ ể
1+n
u
?
c) S d ng quy trình b m phím trên đ tính ử ụ ấ ể
10 21 25 28
, , ,u u u u
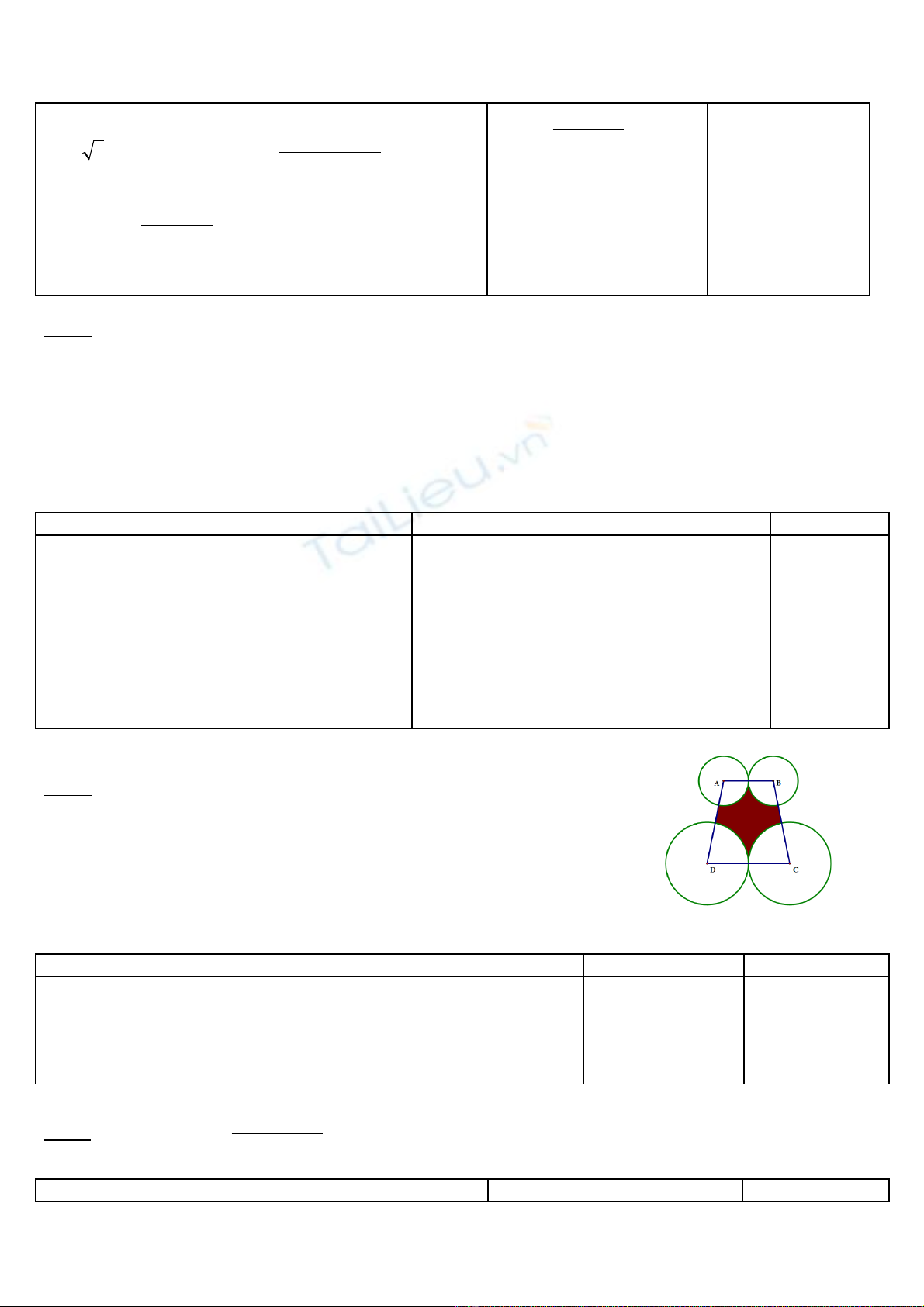
Bài 8: (3 đi m)ể Tính t ng di n tích hình n m gi a hình thang và ngoàiổ ệ ằ ữ
hình tròn (ph n màu đ m) bi t chi u dài hai đáy hình thang là 3m vàầ ậ ế ề
5m, di n tích hình thang b ng 20mệ ằ 2.
Bài 9: (3đi m) Cho hàm s y = ể ố
2
2
2 7 4
5 6
x x
x x
− −
− +
. Tính y(5) t i x = ạ
5
3
1
www.vnmath.com
Bài 10: (3 đi m) Cho t di n ABCD có các c nh AB =ể ứ ệ ạ
27
, BC =
26
,CD =
25
,BD=
24
và chân đ ng vuông góc h t A xu ng m t ph ng (BCD) là tr ng tâm c a tam giác BCD. ườ ạ ừ ố ặ ẳ ọ ủ
Tính VABCD.
Bài 11: (5 đi m)ể Cho ph ng ươ
( )
( )
6
log 47 6 1+ − =
x
x m
a) Tìm các nghi m g n đúng c a ph ng trình khi m = 0,4287ệ ầ ủ ươ
b) Tìm giá tr nguyên l n nh t c a m đ ph ng trình (1) có nghi mị ớ ấ ủ ể ươ ệ
Bài 1 2: (3 đi m)ể Cho đa th c ứ
( ) ( ) ( ) ( ) ( )
2 3 15
1 2 1 3 1 ... 15 1= + + + + + + + +P x x x x x
Đ c vi t d i d ng ượ ế ướ ạ
( )
2 15
0 1 2 15
...= + + + +P x a a x a x a x
. Tìm h s ệ ố
10
a
--------H t-------ế
2
www.vnmath.com
ĐÁP ÁN
www.vnmath.com
Bài 1: Tính g n đúng các nghi m ( đ , phút, giây ) c a ph ng trình ầ ệ ộ ủ ươ
3(sin cos ) 5sin cos 2x x x x+ − =
Cách gi iảK t quế ả Đi mể
Đ t ặ
0
sin cos 2 sin( 45 ), 2t x x x t= + = +
Suy ra
21
sin .cos 2
t
x x −
=
Pt
1
2
2
3 14
5
5 6 1 0
3 14
5
t
t t
t
+
=
− − =� � +
=
0
0
3 14
sin( 45 ) 5 2
3 14
sin( 45 ) 5 2
x
x
+
+ =
−
+ =�
0 0
127 26'32, 75" 360x k +
0 0
262 33'27, 25" 360x k +
0 0
351 1'14, 2" 360x k − +
0 0
4141 1'14, 2" 360x k +
0.5
1
1
0.5
Bài 2: Tính g n đúng giá tr c a a và b n u đ ng th ng ầ ị ủ ế ườ ẳ
y ax b= +
đi qua đi m ể
(5;2)A
và là ti p tuy n c aế ế ủ
Elip
2 2
1
16 9
x y
+ =
Cách gi iảK t quế ả Đi mể
Do đi m ể
(5;2)A
thu c đ ng th ng (d):ộ ườ ẳ
y ax b= +
,
nên ta có 5a + b = 2 (1)
Đi u ki n đ đ ng th ng (d) ti p xúc v iề ệ ể ườ ẳ ế ớ
Elip:
2 2 2 2 2 2 2
16 9A a B b C a b+ = + =�
(2)
Thay (1) vào 2) :
2
9 20 5 0a a− − =
(*)
Vào Equation gi i ph ng trình b c hai (*) taả ươ ậ
đ c k t qu .ượ ế ả
1
1
2, 44907
10, 24533
a
b
−
2
2
0, 22684
3,13422
a
b
−
1
1
1
Bài 3:
(3 đi m) ểCho bi t tanx = tan35ế0.tan360.tan370 ….tan520.tan530 và 00 < x < 900
Tính
2 3 2 3
3 3
tan (1 os ) cot (1 sin )
( os sin )(1 osx + sinx)
x c x x x
Mc x x c
+ + +
=+ +
Cách gi iảK t quế ả Đi mể
3
www.vnmath.com
tanx = tan350 tan360
x = 26,96383125 M= 2,483639682
1
2
Bài 4:
(3 đi m) ểM t s ti n 58000 đ ng đ c g i ti t ki m theo lãi kép. Sau 25 tháng đ c c v n l n l i làộ ố ề ồ ượ ử ế ệ ượ ả ố ẫ ạ
84155 đ. Tính lãi su t/tháng.ấ
Cách gi iảK t quế ả Đi mể
A: s ti n có đ c sau n tháng, a: s ti nố ề ượ ố ề
g i ban đ u, r: lãi su t và n: s thángử ầ ấ ố
Suy ra công th c lãi kép A = a( 1+ r)ứn.
T đây suy raừ
1
nA
ra
= −
. B m máy ta đ c k t quấ ượ ế ả
1,5%
1
1
1
Bài 5:
(3 đi m) ểTính g n đúng giá tr l n nh t và nh nh t c a hàm sầ ị ớ ấ ỏ ấ ủ ố
2sin 3cos 1
cos + 2
x x
yx
+ −
=
Cách gi i ảK t quế ả Đi mể
Ta bi n đ i ế ổ
2sin 3cos 1
cos + 2
x x
yx
+ −
=
về
ph ng trình:ươ
2sinx + (3 – y)cosx =2y + 1
V y pt có nghi m khiậ ệ
( ) ( )
2 2
2
2 3 2 1y y+ − +
. Suy ra:
5 61 5 61
3 3
y
− − − +
4, 270083225 0,936749892y−
1
1
1
Bài 6:
(3 đi m)ể Cho các hàm s ố
2
2 4
2 3 5 2sin
( ) ; ( )
1 1 cos
x x x
f x g x
x x
+ −
= =
+ +
.
Hãy tính giá tr c a các hàm h p ị ủ ợ
và
t i ạ
35x=
.
Cách gi iảK t quế ả Đi mể
4
www.vnmath.com
Đ i đ n v đo góc v Radianổ ơ ị ề
Gán
35
cho bi n X, Tính ế
2
2
2 3 5
1
X X
YX
+ −
=+
, ta đ cượ
giá tr ị
1,523429229Y
và l u vào b nh Y (STO Y),ư ộ ớ
Tính
4
2sin
( ) ( ( )) 1.997746736
1 cos
Y
g Y g f x
Y
= =
+
.
Làm t ng t ta cũng đ c:ươ ự ượ
( ( )) 1,784513102f g x
4
2sin
( ) 1 cos
( ( )) 1.997746736
=+
=
Y
g Y Y
g f x
( ( )) 1,784513102f g x
1
1
1
Bài 7:
(5 đi m) ểCho dãy s ố
n
u
xác đ nh b i: ị ở
( )
1 2 3 1 1 2
1; 2; 3;...; 2 3 3
+ − −
= = = = + +
n n n n
u u u u u u u n
a) Tính giá tr c a ị ủ
4 5 6 7
, , ,u u u u
b) Vi t quy trình b m phím đ tính ế ấ ể
1+n
u
?
c) S d ng quy trình b m phím trên đ tính ử ụ ấ ể
10 21 25 28
, , ,u u u u
Cách gi i ảK t quế ả Đi mể
a)
1 2 6 7
10; 22; 51; 125= = = =u u u u
b) Quy trình b m phímấ
Nh p bi u th c:ậ ể ứ
X = X + 1 : D = C + 2B + 3A :A= = B: B = C:
C = D
V i các giá tr ban đ u: X = 3; A = 1; B = 2; Cớ ị ầ
= 3
a)
1 2
6 7
10; 22;
51; 125
= =
= =
u u
u u
c)
10 21
25
28
1657; 22383417;
711474236;
9524317645
= =
=
=
u u
u
u
1
1
1
Bài 8: (3 đi m)ể Tính t ng di n tích hình n m gi a hình thang và ngoàiổ ệ ằ ữ
hình tròn (ph n màu đ m) bi t chi u dài hai đáy hình thang là 3m vàầ ậ ế ề
5m, di n tích hình thang b ng 20mệ ằ 2.
Cách gi iảK t quế ả Đi mể
Di n tích hình thang: 20mệ2.
Di n tích m t qu t l n: Sệ ộ ạ ớ qu t l n ạ ớ = 4.2919 m2.
Di n tích m t qu t nh : Sệ ộ ạ ỏ qu t nhạ ỏ = 1.9829 m2.
Di n tích ph n c n tìm: S = Sệ ầ ầ hình thang – 2(Squ t l n ạ ớ + Squ t nhạ ỏ)
7.4378cm21
1
1
Bài 9 : Cho hàm s y = ố
2
2
2 7 4
5 6
x x
x x
− −
− +
. Tính y(5) t i x = ạ
5
3
Cách gi iảK t quế ả Đi mể
5