http://www.vnmath.com
S Gíao d c & Đào t oở ụ ạ
t nh Vĩnh Phúcỉ
Tr ng THPT Xuânườ
Hoà
KỲ THI KSCL THI Đ I H C NĂM 2011 L N TH 1Ạ Ọ Ầ Ứ
Đ THI MÔN Toán; Kh i AỀ ố
Th i gian làm bài : 180 phút, không k th i gian giao đ .ờ ể ờ ề
Đ thi g m 01 trangề ồ
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
I/- PH N CHUNG CHO T T C THÍ SINH (Ầ Ấ Ả 7, 0 đi m)ể
Câu I (2,0 đi m)ể: Cho hàm s ố
4 2 2
2 1 (1)y x m x= + +
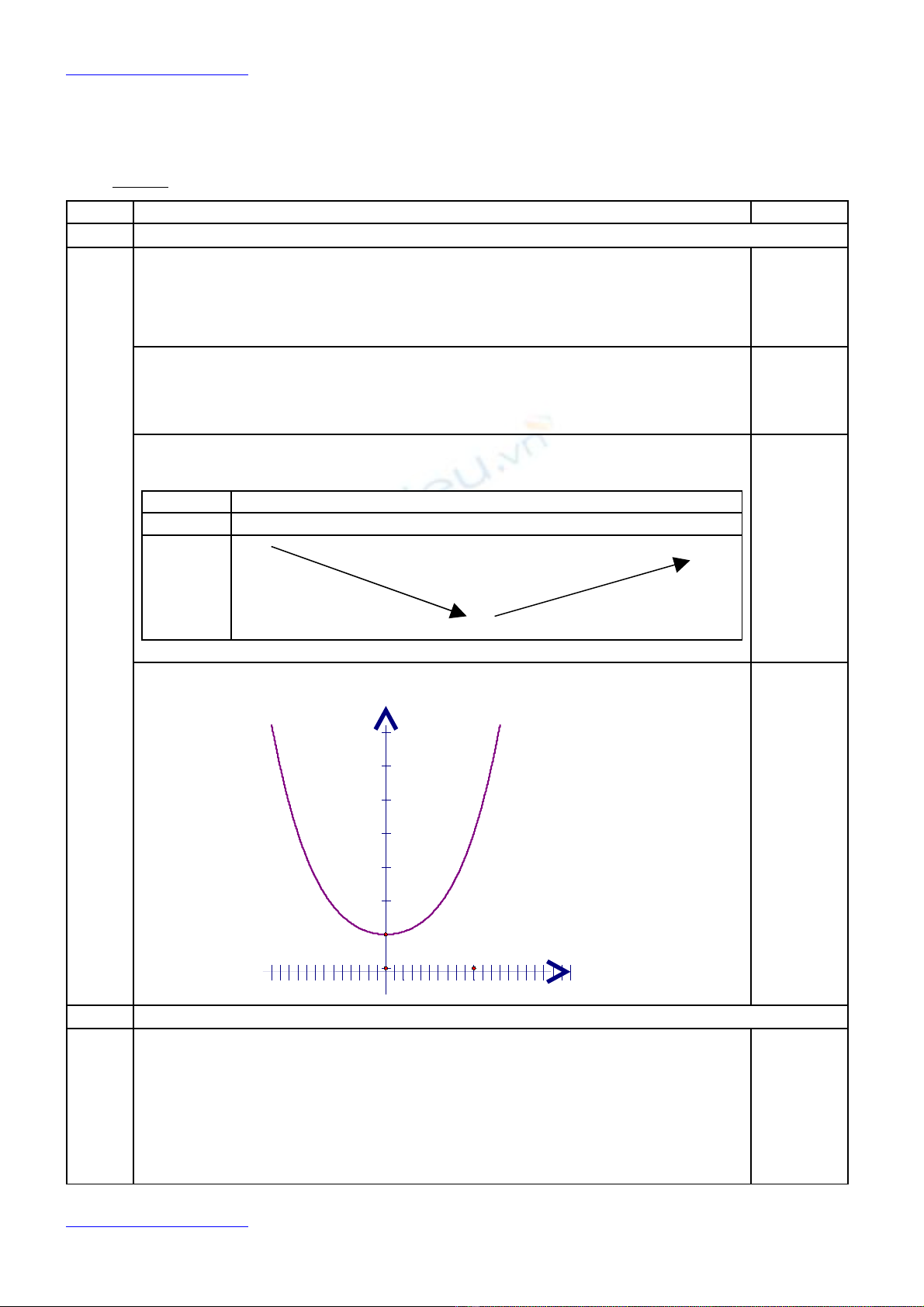
1. Kh o sát s bi n thiên và v đ th c a hàm s (1) khi m = 1.ả ự ế ẽ ồ ị ủ ố
2. Ch ng minh r ng đ ng th ng y = x + 1 luôn c t đ th c a hàm s (1) t i hai đi m phânứ ằ ườ ẳ ắ ồ ị ủ ố ạ ể
bi t v i m i giá tr c a m.ệ ớ ọ ị ủ
Câu II (2,0 đi m)ể:
1. Gi i ph ng trình: ả ươ
sin 4 cos 4 1 4(sin cos )x x x x− = + −
2. Gi i h ph ng trình: ả ệ ươ
3 3
2 2
4 16
1 5(1 )
x y y x
y x
+ = +
+
++ = +
+
Câu III (1,0 đi mể): Tính gi i h n ớ ạ
2
0
1 cos 2 tan
lim .sin
x
x x
x x
x
− +
Câu IV (1,0 đi mể): Trong không gian, cho tam giác vuông cân ABC có c nh huy n ạ ề
AB = 2a. Trên đ ng th ng ươ ẳ d đi qua A và vuông góc v i m t ph ng ớ ặ ẳ (ABC) l y đi m ấ ể S, sao cho
m t ph ng ặ ẳ (SBC) t o v i m t ph ng ạ ớ ặ ẳ (ABC) m t góc ộ600 . Tính di n tích m t c u ngo i ti p tệ ặ ầ ạ ế ứ
di n ệSABC.
Câu V (1,0 đi mể): Tìm giá tr nh nh t c a hàm sị ỏ ấ ủ ố
4 3 2
2
4 8 8 5
( ) 2 2
x x x x
f x x x
− + − +
=− +
II. PH N RIÊNG(Ầ3,0 đi mể): Thí sinh ch đ c làm m t trong ph n ( ph n A ho c ph n B)ỉ ượ ộ ầ ầ ặ ầ
A. Theo ch ng trình Chu nươ ẩ
Câu VIa (2,0 đi m)ể
1. Trong m t ph ng v i h to đ ặ ẳ ớ ệ ạ ộ 0xy, cho elíp (E) có tiêu đi m th nh t ể ứ ấ
( 3; 0)−
và đi qua
đi m ể
4 33
(1; )
5
M
. Hãy xác đ nh to đ các đ nh c a ị ạ ộ ỉ ủ (E).
2. Gi i ph ng trình: ả ươ
.
Câu VII a (1,0 đi mể): Có bao nhiêu s t nhiên có 4 ch s khác nhau và khác 0 mà trong m iố ự ữ ố ỗ
s luôn có m t hai ch s ch n và hai ch s l .ố ặ ữ ố ẵ ữ ố ẻ
B. Theo ch ng trình Nâng caoươ
Câu VI.b(2,0 đi m)ể
1. Trong m t ph ng v i h to đ ặ ẳ ớ ệ ạ ộ 0xy, cho đi m ểA(2; 1). L y đi m ấ ể B n m trên tr c hoànhằ ụ
có hoành đ không âm sao cho tam giác ộABC vuông t i ạA. Tìm to đ ạ ộ B, C đ tam giác ểABC có
di n tích l n nh t.ệ ớ ấ
2. Có bao nhiêu s t nhiên có 5 ch s khác nhau và khác 0 mà trong m i s luôn có m tố ự ữ ố ỗ ố ặ
hai ch s ch n và ba ch s l .ữ ố ẵ ữ ố ẻ
Câu VII.b(1,0 đi mể): Tìm
m
đ hàm s : ể ố
21mx
yx
−
=
có hai đi m c c tr ể ự ị A, B và đo n ABạ
ng n nh t.ắ ấ
-------------------------H t--------------------------ế
Thí sinh không đ c s d ng tài li u. Cán b coi thi không gi i thích gì thêm.ượ ử ụ ệ ộ ả
http://www.vnmath.com
1
http://www.vnmath.com
H và tên thí sinh:…………………………………; S báo danh:………………..ọ ố
ĐÁP ÁN, BI U ĐI M Ể Ể
MÔN TOÁN Kh i ốA
L u ý :ư H c sinh làm theo cách khác mà đúng v n cho đi m t i đaọ ẫ ể ố
Câu Đáp án Đi mể
I 1. (1, 0 đi m). ểKh o sát….ả
V i m=1, hàm s tr thành: ớ ố ở
4 2
2 1y x x= + +
* T p xác đ nh: Rậ ị
* S bi n thiênự ế
+
3 2
' 4 4 4 ( 1) ' 0 0y x x x x y x= + = + = =� �
0, 25
Ta có:
' 0 0; ' 0 0y x y x> > < <� �
Hàm s ngh ch bi n trong kho ng ố ị ế ả
( )
;0−0
và đ ng bi n trong kho ngồ ế ả
( )
0; +;
; đ t c c ti u t i x=0; y(0)=1ạ ự ể ạ
0, 25
+ Gi i h n: ớ ạ
lim lim
x x
y y
y−ml +m
= = +l
B ng bi n thiên: ả ế
x
−=
0
+
y' - 0 +
y
+
+
1
0, 25
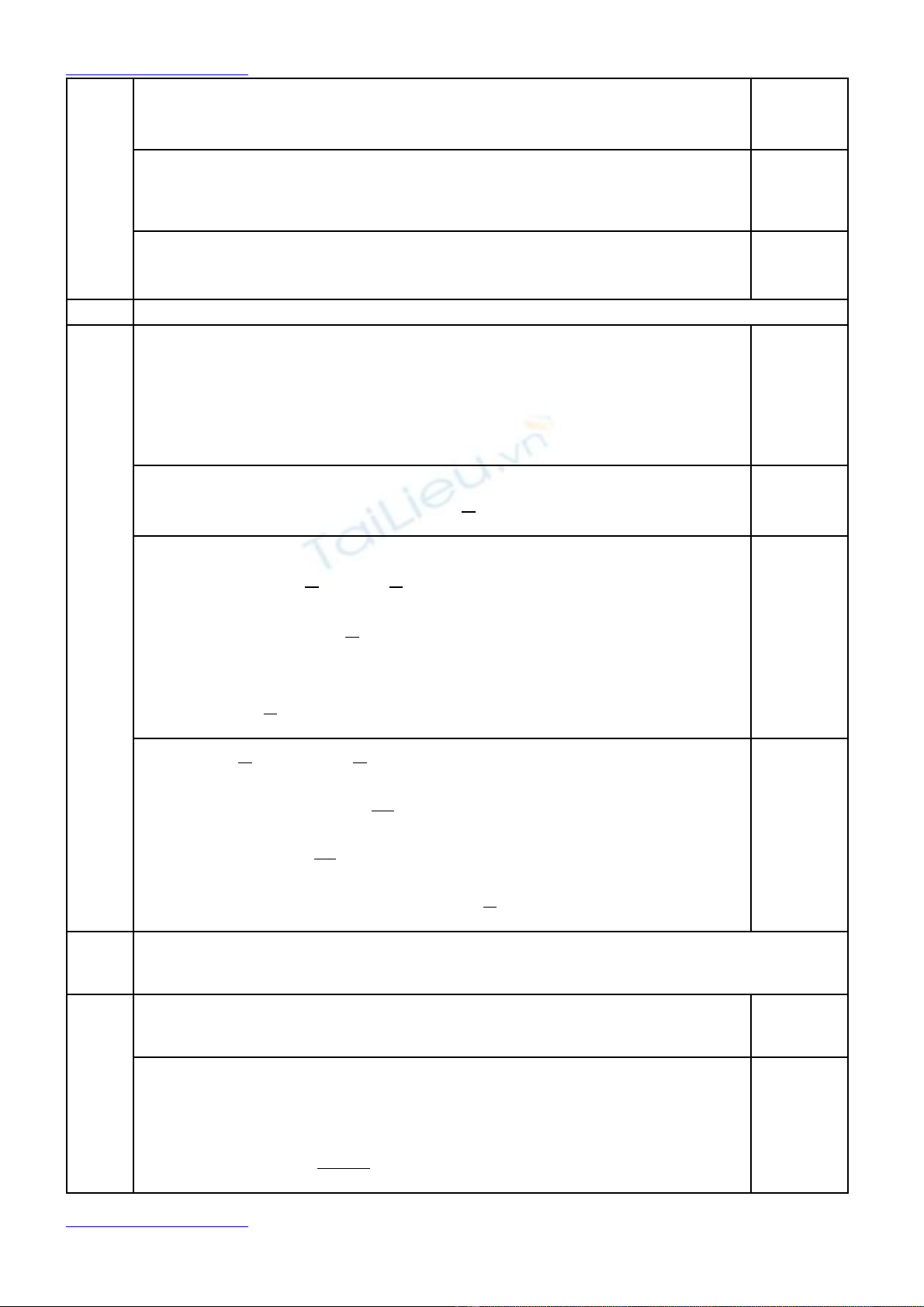
* Đ th : Hàm s đã cho là hàm s ch n nên đ th nh n tr c tung làm tr cồ ị ố ố ẵ ồ ị ậ ụ ụ
đ i x ng.ố ứ
0,25
2. ((1, 0 đi m).ể Ch ng minh đ ng th ng ….ứ ườ ẳ
S giao đi m c a hai đ th t ng ng v i s nghi m c a ph ng trình: ố ể ủ ồ ị ươ ứ ớ ố ệ ủ ươ
4 2 2
2 1 1x m x x+ + = +
3 2
( 2 1) 0x x m x+ − =�
(*)
3 2
0
2 1 0(**)
x
x m x
=
=
=+ − =
+
Ph ng trình (*) có m t nghi m ươ ộ ệ
x = 0
0,25
http://www.vnmath.com
6
4
2
-1 12
2
http://www.vnmath.com
Ta s đi ch ng minh ph ng trình: ẽ ứ ươ
3 2
2 1 0x m x+ − =
(**) có đúng m t nghi mộ ệ
khác 0 v i m i giá tr mớ ọ ị
* N u m=0 thì pt(**) tr thành: ế ở
3
1 0 1x x− = =� �
pt(*) có đúng 2 nghi m.ệ
0,25
•N u ế
0m
m
, Xét hàm s ố
3 2
( ) 2 1f x x m x= + −
trên R.
•Ta có:
2 2
'( ) 3 2 0,f x x m x R= + > ∀x
=
f(x) luôn đ ng bi n trên Rồ ế
( ) 0f x =�
có nhi u nh t m t nghi m.ề ấ ộ ệ
0,25
Ta có: f(0) = -1; f(1) =2m2 >0
(0). (1) 0f f <� �
pt
( ) 0f x =
có nhi u nh tề ấ
m t nghi m thu c (0; 1).ộ ệ ộ
V y pt (**) có đúng m t nghi m khác 0ậ ộ ệ
ệ
(đpcm)
0,25
II 1. (1, 0 đi m).ể Gi i ph ng trình: ả ươ
sin 4 cos 4 1 4(sin cos )x x x x− = + −
(1)
ĐK:
x R∀R
[ ]
2
2 2
(1) sin 4 1 cos 4 4(sin cos )
2sin 2 .cos 2 2 cos 2 4(cos sin )
(cos sin )(cos 2 sin 2 ) 2(cos sin ) 0
(cos sin ) (cos sin )(cos 2 sin 2 ) 2 0 (2)
x x x x
x x x x x
x x x x x x
x x x x x x
= + + −�
= − −�
− − − − =�
− + − − =�
0,25
Xét hai kh năng x y ra cho (2):ả ả
* TH1:
cos sin 0 tan 1 4
x x x x k
ππ
− = = = +� �
0,25
* TH2:
(cos sin )(cos 2 sin 2 ) 2 0
2cos(2 ).cos( ) 2 0
4 4
cos3 cos( ) 2 (*)
2
x x x x
x x
x x
π π
π
− − − =
+ − − =�
+ + =�
cos3 1 (3)
cos( ) 1 (4)
2
x
x
π
=
=
=
==+ =
+
+
0,25
Xét:
cos( ) 1 2
2 2
x x m
π π π
+ = = − +�
3
3 6
2
x m
ππ
= − +�
Lúc đó:
3
cos3 cos( 6 ) 0
2
x m
ππ
= − + =
( Vô lý v i (3))ớ
V y (*) vô nghi m., nên (1) có nghi m: ậ ệ ệ
4
x k
ππ
= +
0,25.
2.(1, 0 đi m).ể Gi i h ph ng trình: ả ệ ươ
3 3
2 2
4 16
1 5(1 )
x y y x
y x
y+ = +
+
++ = +
+
+
HPT
2 2 2 2
2 2 2 2
( 16) ( 4) ( 16) 5 (1)
4 5 4 5 (2)
x x y y x x x y
y x y x
� �
− = − − =
� �
� �
� �
− = − =
� �
� �
0,25
Pt (1)
2
0
16 5 (3)
x
x xy
=
=
==− =
−
+) x = 0 thay vào (2) ta đ c ượ
2y==
+)
0x
x
, pt (3)
2
16
5
x
yx
−
=�
thay vào (2) ta đ c:ượ
0,5
http://www.vnmath.com
3
S
A
C
B
http://www.vnmath.com
4 2 2
124 132 256 0 1x x x+ − = =�
•N u x = 1 thì y = -3ế
•N u x =-1 thì y = 3.ế
V y HPT có các nghi m: (x; y) =( 0; 2); (0; -2); (1; -3); (-1; 3).ậ ệ
0,25
III (1, 0 đi mể) Tính gi i h n: I= ớ ạ
2
0
1 cos 2 tan
lim .sin
x
x x
x x
x
− +
2
2
2
0
sin
2sin cos
lim .sin
x
x
xx
Ix x
x
+
=
0,5
2
0
2sin sin
lim( ) 2 1 3
.cos
x
x x
Ix x x
x
= + = + =
0,5
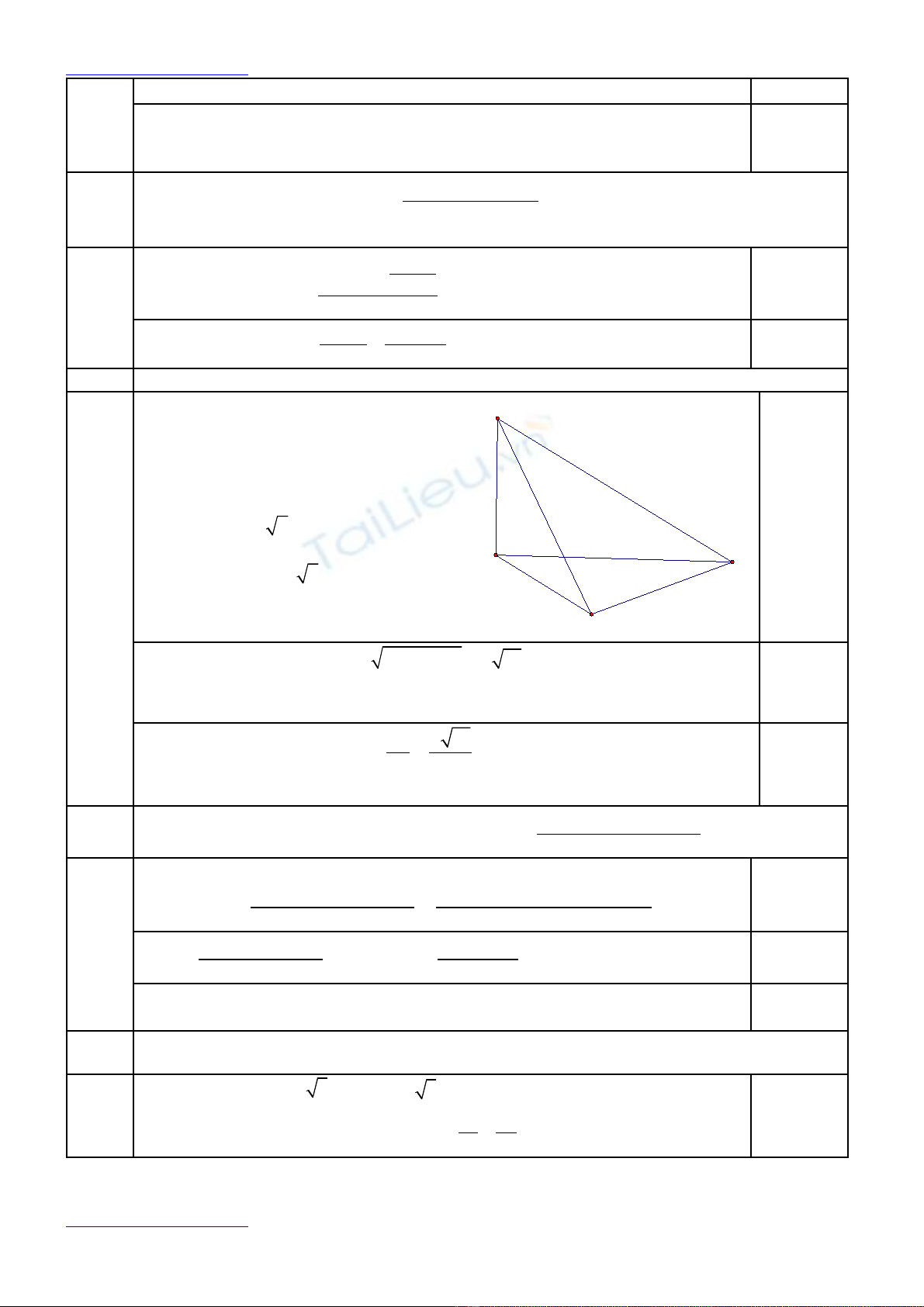
IV (1 đi m):ể Tính di n tích m t c u ngo i ti p t di n ệ ặ ầ ạ ế ứ ệ SABC.
T gi thi t suy ra ừ ả ế
ABC
∆
vuông t i C k t h p v i ạ ế ợ ớ
( )d SAC⊥
.
Suy ra
( )BC SAC⊥
Do đó
D
0
60SCA =
Do
ABC∆
vuông t i C và ạAB =2a
2AC BC a= =�
Trong tam giác vuông SAC ta có
0
.tan 60 6SA AC a= =
0,5
Trong tam giác SAB có:
2 2
10SB SA AB a= + =
Do
D
D
0
90SCB SAB= =
nên t di n SABC n i ti p trong m t c u đ ng kínhứ ệ ộ ế ặ ầ ườ
SB. 0,25
Suy ra bán kính m t c u b ngặ ầ ằ
10
2 2
SB a
=
V y Sậ
2 2
4 10
mc
R a
π π
= =
(Đ.V.D.T)
0,25
V (1 đi m):ể Tìm giá tr nh nh t c a hàm s : ị ỏ ấ ủ ố
4 3 2
2
4 8 8 5
( ) 2 2
x x x x
f x x x
− + − +
=− +
T p xác đ nh c a hàm s là R. ậ ị ủ ố
Ta có:
4 3 2
2
4 8 8 5
( ) 2 2
x x x x
f x x x
− + − +
=− +
=
222
2
( 2 ) 4( 2 ) 4 1
2 2
x x x x
x x
− − − + +
− +
0,5
2 2
2 2
2 2
( 2 2) 1 1
( ) 2 2 2( 2 2 0
2 2 2 2
x x
f x x x do x x
x x x x
− + +
= = − + +o− + >
− + − +
)0,25
Đ ng th c x y ra ẳ ứ ả
2
2 2 1 1x x x− + = =� �
.
V y Minf(x) = 2 khi x =1ậ
0,25
Vi.a 1.(1 đi m):ể Hãy xác đ nh to đ các đ nh c a ị ạ ộ ỉ ủ (E).
(E) có tiêu đi m ể
1
( 3; 0)F−
nên
3c=
Ph ng trình chính t c c a (E) có d ng: ươ ắ ủ ạ
2 2
2 2
1
x y
a b
+ =
(a>b>0)
0,25
http://www.vnmath.com
4
http://www.vnmath.com
Ta có:
4 33
(1; )
5
M
2 2
1 528
( ) 1(1)
25
Ea b
+ =� �
và
2 2 2 2
3a b c b= + = +
thay vào
(1) ta đ c: ượ
4 2
2 2
1 528 1 25 478 1584 0
3 25 b b
b b
+ = − − =�
+
2
22 22b b= =� �
0,5
Suy ra:
2
25 5a a= =�
. V y (E) có b n đ nh là: (-5;0); (5; 0); (0;- ậ ố ỉ
22
); (0;
22
)
0,25
2. (1,0 đi m): ểGi i ph ng trình: ả ươ
2.27 18 4.12 3.8
x x x x
+ = +
.
Ta có PT
3 2 2 3
2.3 2 .3 4.2 3 3.2
x x x x x x
+ = +�
. 0,25
Chia c hai v cho ả ế
3
2 0
x
>
: PT
3 2
3 3 3
2 4 3 0
2 2 2
x x x
� � � � � �
+ − − =�� � � � � �
� � � � � �
.0,25
Đ t ặ
3
2
x
t
� �
=� �
� �
, đk: t>0. PT tr thành:ở
( )
( )
3 2 2
2 4 3 0 1 2 3 0
1
3
2
t t t t t t
t
t
+ − − = + − − =�
= −
=
=
===
=
.
Do t >0 nên t=
3
2
0,25
Khi
3
2
t
=
, ta có:
3 3 1
2 2
x
x
� �= =�
� �
� �
. KL: Nghi m PT là ệ
1x
=
.0,25
ViIa(1,0 đi m).ể Có bao nhiêu s t nhiên có 4 ch s khác nhau và khác 0 màố ự ữ ố
trong m i s luôn có m t hai ch s ch n và hai ch s l .ỗ ố ặ ữ ố ẵ ữ ố ẻ
T gi thi t bài toán ta có ừ ả ế
6
2
4
=
C
cách ch n 2 ch s ch n (vì không có s 0)ọ ữ ố ẵ ố
và
10
2
5
=
C
cách ch n hai ch s l => cã ọ ữ ố ẻ
2
5
C
.
2
5
C
= 60 b 4 s tho mãn bàiộ ố ả
toán.
0,5
M i b 4 s nh th có 4! s đ c thành l p. V y có t t c ỗ ộ ố ư ế ố ượ ậ ậ ấ ả
2
4
C
.
2
5
C
.4! =
1440 s .ố
0,5
VI.b 1. (1 đi m):ể Tìm to đ ạ ộ B, C đ tam giác ểABC có di n tích l n nh t.ệ ớ ấ
G i A(2; 1); B(b; 0); C(0; c); b, c > 0.ọ
Theo gi thi t ta có tam giác ABC vuông t i A nênả ế ạ
5
. 0 2 5 0 2
AB AC c b O b= = − +� � � � �
uuur uuur
0,25
2 2 2
1 1
. ( 2) 1. 2 ( 1)
2 2
ABC
S AB AC b c
∆
= = − + + −
2 2
( 2) 1 4 5b b b= − + = − +
0,5
Do
max
5
02
b SbSx
khi b =0. Suy ra B(0; 0); C(0; 5). 0,25
2.(1 đi m):ể Có bao nhiêu s t nhiên có 5 ch s khác nhau và khác 0 mà trong m i số ự ữ ố ỗ ố
luôn có m t hai ch s ch n và hai ch s lặ ữ ố ẵ ữ ố ẻ
http://www.vnmath.com
5