Hóa h c đ i c ng 1 Gi ng viên: Ths Nguy n Vănọ ạ ươ ả ễ
Quang
Ho t đ ng c a GV và SVạ ộ ủ N i dung bài d yộ ạ
D a vào hàm sóng và các đi u ki nự ề ệ
v hàm sóng hãy nêu n i dung c aề ộ ủ
tiên đ v hàm sóng? ề ề
- Mô t đ y đ m i tr ng thái c aả ầ ủ ỗ ạ ủ
m t h l ng t , ta dùng hàm sóngộ ệ ượ ử
hay hàm tr ng thái ạ
( )
q
ψ
, là m tộ
hàm xác đ nh c a to đ q. Hàm nàyị ủ ạ ộ
nói chung là ph c, đ n tr , h u h n,ứ ơ ị ữ ạ
liên t c, kh vi. Bình ph ngụ ả ươ
mođun hàm đó cho bi t xác su t tìmế ấ
th y h l ng t tr ng thái t iấ ệ ượ ử ở ạ ạ
m t đi m có to đ q trong khôngộ ể ạ ộ
gian ng v i kho ng xác đ nh c aứ ớ ả ị ủ
hàm này.
Bài 1: TIÊN Đ V HÀM SÓNGỀ Ề
I. N i dungộ
- M i tr ng thái đ y đ c a m t h l ng t đ cỗ ạ ầ ủ ủ ộ ệ ượ ử ượ
mô t đ y đ b ng m t hàm ả ầ ủ ằ ộ
( )
,q t
ψ
- là hàm xác đ nhị
to đ khái quát q và th i gian t - đ c g i là hàmạ ộ ờ ượ ọ
sóng hay hàm tr ng thái. Hàm sóng ạ
( )
,q t
ψ
không có ý
nghĩa v t lí tr c ti p, song bình ph ng mođun c aậ ự ế ươ ủ
hàm đó
( )
2
,q t
ψ
, cho bi t xác su t tìm th y h l ngế ấ ấ ệ ượ
t t i m t th i đi m trong không gian có to đ q ử ạ ộ ờ ể ạ ộ ở
th i đi m t. Hàm ờ ể
( )
2
,q t
ψ
đ c g i là hàm m t đượ ọ ậ ộ
xác su t.ấ
- Đi u ki n hàm sóng:ề ệ
+ Hàm
( )
,q t
ψ
nói chung là hàm s ph cố ứ
+ Hàm
( )
,q t
ψ
ph i là hàm đ n trả ơ ị
+ Hàm
( )
,q t
ψ
ph i h u h n, có giá tr trong m tả ữ ạ ị ộ
kho ng xác đ nh [a,b]ả ị
+ Hàm
( )
,q t
ψ
ph i là hàm liên t cả ụ
+ Hàm
( )
,q t
ψ
ph i là hàm kh viả ả
II. S chu n hoá hàm sóngự ẩ
- Đi u ki n chu n hoá hàm sóng:ề ệ ẩ
dP
∫
=
( )
2
,1
q t dV
ψ
=
∫
N u hàm này là hàm ph c thì: ế ứ
( ) ( )
*.dP q q dV
ψ ψ
=
Xác su t tìm th y h l ng t trong c không gianấ ấ ệ ượ ử ả
quy đ nh b i [a,b]ị ở
*( ). ( ) 1q q dV
ψ ψ
=
∫
- Ngoài ra hàm sóng còn ph i tho mãn đi u ki nả ả ề ệ
tr c giao. ự
Khoa T Nhiên – Tr ng Cao đ ng S ph m Qu ng Ninhự ườ ẳ ư ạ ả
Hóa h c đ i c ng 1 Gi ng viên: Ths Nguy n Vănọ ạ ươ ả ễ
Quang
Có các hàm: f1, f2…fi, fj… Hai hàm fi, fj đ c g i làượ ọ
tr c giao v i nhau n u chúng tho mãn đi u ki n:ự ớ ế ả ề ệ
- H hàm v a là các hàm chu n hóa v a là các hàmệ ừ ẩ ừ
tr c giao g i là h hàm tr c chu n. Kí hi u g p l iự ọ ệ ự ẩ ệ ộ ạ
là:
*
ij
1
.0
j
i
khi i j
f f dV khi i j
δ
≡
= =
≠
∫
3. Nguyên lí ch ng ch t tr ng tháiồ ấ ạ
- N u m t h l ng t vào tr ng thái đ c mô tế ộ ệ ượ ử ở ạ ượ ả
b i hàm sóng ở
( )q
ψ
thì tr ng thái đó cũng có th đ cạ ể ượ
mô t b i hàm sóng c.ả ở
( )q
ψ
, v i c là h ng s th a s .ớ ằ ố ừ ố
- N u m t h l ng t có th vào tr ng tháiế ộ ệ ượ ử ể ở ạ
đ c mô t b i hàm sóng ượ ả ở
1( )q
ψ
ho c vào tr ng tháiặ ạ
đ c mô t b i hàm sóng ượ ả ở
2( )q
ψ
thì h l ng t đó cóệ ượ ử
th đ c mô t b i hàm sóng ể ượ ả ở
( )q
ψ
mà:
( )q
ψ
=c1.
1( )q
ψ
+ c2.
2( )q
ψ
c1, c2 đ c g i là các h s t h p hàm sóng.ượ ọ ệ ố ổ ợ
T ng quát:ổ
( )q
ψ
=c1.
1( )q
ψ
+c2.
2( )q
ψ
+c3.
3( )q
ψ
+c4.
4( )q
ψ
+…+
ci.
( )i q
ψ
+…
Bài 2: TIÊN Đ V TOÁN TỀ Ề Ử
Ho t đ ng c a GV và SVạ ộ ủ N i dung bài d yộ ạ
Toán t là m t quy t c, m tử ộ ắ ộ
phép toán mà khi nó tác d ngụ
vào m t hàm s thu đ cộ ẽ ượ
m t hàm m iộ ớ
I. N i dung c a tiên độ ủ ề
T ng ng v i m i đ i l ng v t lí A c a h l ngươ ứ ớ ỗ ạ ượ ậ ủ ệ ượ
t , vào tr ng thái đ c mô t b i hàm ử ở ạ ượ ử ở
( )
q
ψ
, có m tộ
toán t tuy n tính Hecmit ử ế
µ
A
. Tr trung bình ị
A
hay
A
Khoa T Nhiên – Tr ng Cao đ ng S ph m Qu ng Ninhự ườ ẳ ư ạ ả
Hóa h c đ i c ng 1 Gi ng viên: Ths Nguy n Vănọ ạ ươ ả ễ
Quang
Toán t kí hi u: ử ệ
µ
A
, ta có:
µ
( )
A f g=
Khi có
µ
( )
.A f a f=
(1)
f: là hàm riêng c a toán t ủ ử
µ
A
,
a : tr riêng c a toán t ị ủ ử
µ
A
v i hàm riêng fớ
(1): là ph ng trình hàmươ
riêng tr riêngị
Ví dụ: Bi t r ng m t vi h tế ằ ộ ạ
chuy n đ ng v i v n t c vể ộ ớ ậ ố
thì bi u th c đ ng năngể ứ ộ
2
1
2
T mv=
ur r
, xung l ngượ
P mv=
ur r
, bi u th c các toán tể ứ ử
thành ph n xung l ng làầ ượ
µ
x
Pi
=h
d
dx
;
µ
y
Pi
=h
d
dy
;
µ
z
Pi
=h
d
dz
Hãy thi t l p bi u th c c aế ậ ể ứ ủ
toán t đ ng năng ử ộ
µ
T
?
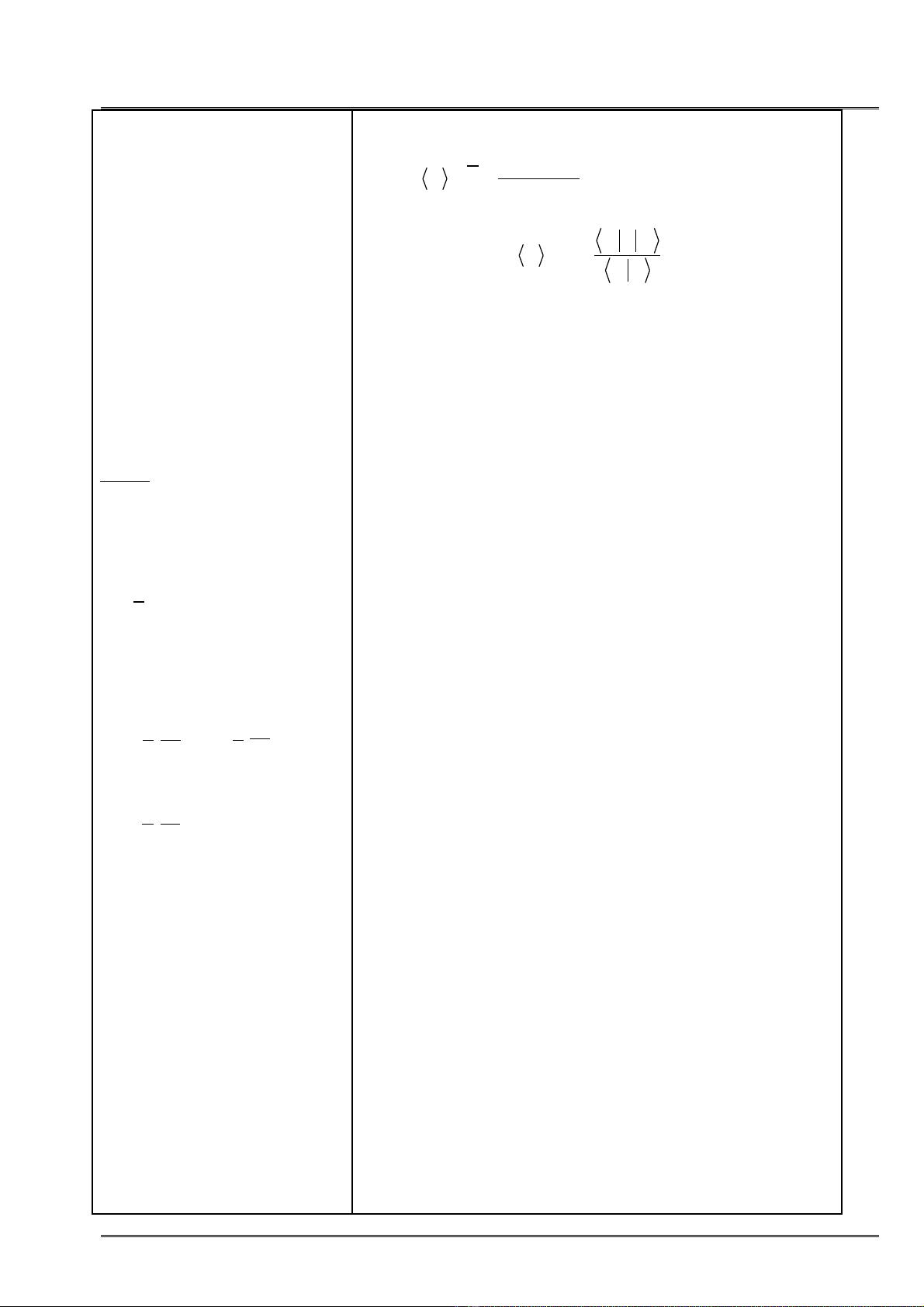
c a đ i l ng A đó đ c tính theo bi u th củ ạ ượ ượ ể ứ
µ
*
*
A dV
A A dV
ψ ψ
ψ ψ
= = ∫∫
Hay kí hi u Đirăc: ệ
µ
A
A A
ψ ψ
ψ ψ
= =
II. Các toán t Hecmit th ng dùng trong hoá h cử ườ ọ
l ng tượ ử
-Toán t to đ : ử ạ ộ
r
r
-Toán t xung l ng:ử ượ
P
ur
(
P
ur
= m
v
r
)
-Toán t momen đ ng l ng: ử ộ ượ
M
uur
(
M
uur
=
P
ur
.
r
r
)
-Toán t năng l ng:ử ượ
+ Th năng: ế
µ
( ) ( )
U r hayU u
r r
+ Đ ng năng: ộ
µ
T
-Toán t Hamint n: ử ơ
µ
µ
µ
H T U= +
. Đây là toán t quanử
tr ng nh t.ọ ấ
III. Các đ i l ng v t lí có tr đ ng th i xác đ nh ạ ượ ậ ị ồ ờ ị ở
cùng m t tr ng thái c a h l ng tộ ạ ủ ệ ượ ử
1. Hai toán t giao hoánử
µ µ
,A B
là hai hoán t tuy n tính Hecmit. Hai toán t đóử ế ử
đ c g i là giao hoán t v i nhau khi giao hoán t c aượ ọ ử ớ ử ủ
chúng b ng 0ằ
µ µ µ µ µ µ
, 0A B AB B A
= − =
Hai toán t giao hoán có chung nhau nh ng hàm riêngử ữ
Khoa T Nhiên – Tr ng Cao đ ng S ph m Qu ng Ninhự ườ ẳ ư ạ ả
Hóa h c đ i c ng 1 Gi ng viên: Ths Nguy n Vănọ ạ ươ ả ễ
Quang
và tr riêng t ng ng đ ng th i tr ng thái mô t b iị ươ ứ ồ ờ ở ạ ả ở
hàm riêng chung đó
2. Các đ i l ng v t lí có tr đ ng th i xác đ nh ạ ượ ậ ị ồ ờ ị ở
cùng m t tr ng thái c a h l ng t .ộ ạ ủ ệ ượ ử
a. Hai toán t giao hoán ử
Hai toán t giao hoán có chung nhau nh ng hàm riêngử ữ
và tr riêng t ng ng đ ng th i xác đ nh tr ng tháiị ươ ứ ồ ờ ị ở ạ
đ c mô t b i hàm riêng đó.ượ ả ở
b. Các đ i l ng v t lí có tr đ ng th i xác đ nhạ ượ ậ ị ồ ờ ị
Đi u ki n c n và đ đ hai đ i l ng v t lí c a hề ệ ầ ủ ể ạ ượ ậ ủ ệ
l ng t có tr xác đinh đ ng th i m t tr ng thái là haiượ ử ị ồ ờ ở ộ ạ
toán t Hecmit t ng ng v i hai đ i l ng đó giao hoánử ươ ứ ớ ạ ượ
v i nhauớ
BÀI 3. TIÊN Đ V PH NG TRÌNH SROĐINGỀ Ề ƯƠ Ơ
H T CHUY N Đ NG T DO TRONG H P TH CH NH T M T CHI UẠ Ể Ộ Ự Ộ Ế Ữ Ậ Ộ Ề
Ho t đ ng c a GV và SVạ ộ ủ N i dung bài d yộ ạ
? Th nào là tr ng thái d ng?ế ạ ừ
- Tr ng thái d ng là tr ng tháiạ ừ ạ
mà năng l ng c a h khôngượ ủ ệ
ph i là m t hàm s c a th iả ộ ố ủ ờ
gian t
? Nh c l i toán t Hamnit nắ ạ ử ơ
I. Ph ng trình Srođingươ ơ
-Tiên đ : Khi m t h l ng t tr ng thái d ngề ộ ệ ượ ử ở ạ ừ , tr ngạ
thái mà toán t Haminton không ph thu c t ng minh vàoử ụ ộ ườ
th i gian t, gi a toán t Hamint n c a h , hàm sóng ờ ữ ử ơ ủ ệ
→)(r
ψ
mô t tr ng thái c a h và năng l ng toàn ph n electronả ạ ủ ệ ượ ầ
có liên h :ệ
)(.)( →→∧ =rErH
ψψ
<1>
<1>: ph ng trình hàm riêng, tr riêngươ ị
Ta l i có : ạ
),,( →→→→
zyxr
vi t g n (x,y,z)ế ọ
=
∧
T
++− 2
2
2
2
2
22
2dz
d
dy
d
dx
d
m
Th năng U có t ng ng toán t ế ươ ứ ử
),,( zyxU
→
Khoa T Nhiên – Tr ng Cao đ ng S ph m Qu ng Ninhự ườ ẳ ư ạ ả
Hóa h c đ i c ng 1 Gi ng viên: Ths Nguy n Vănọ ạ ươ ả ễ
Quang
- Đi u ki n c a gi ng th m tề ệ ủ ế ế ộ
chi u?ề
- Thay bi u th c và gi iể ứ ả
=>
=
∧
H
++− 2
2
2
2
2
22
2dz
d
dy
d
dx
d
m
+
),,( zyxU
thay vào <1>
( )
),,(. zy,x, U
dz
d
dy
d
dx
d
2m
-
2
2
2
2
2
22
zyx
ψ
+
+
= E.
),,( zyx
ψ
↔
),,(.
2
2
2
2
2
2
zyx
zyx
ψ
∂
∂
+
∂
∂
+
∂
∂
+
( )
),,(.),,(
2zyxzyxUE
m
ψ
−
=0
↔
2
∇
.
),,( zyx
ψ
+
( )
),,(.),,(
2zyxzyxUE
m
ψ
−
=0
Ph ng trình Srođingươ ơ
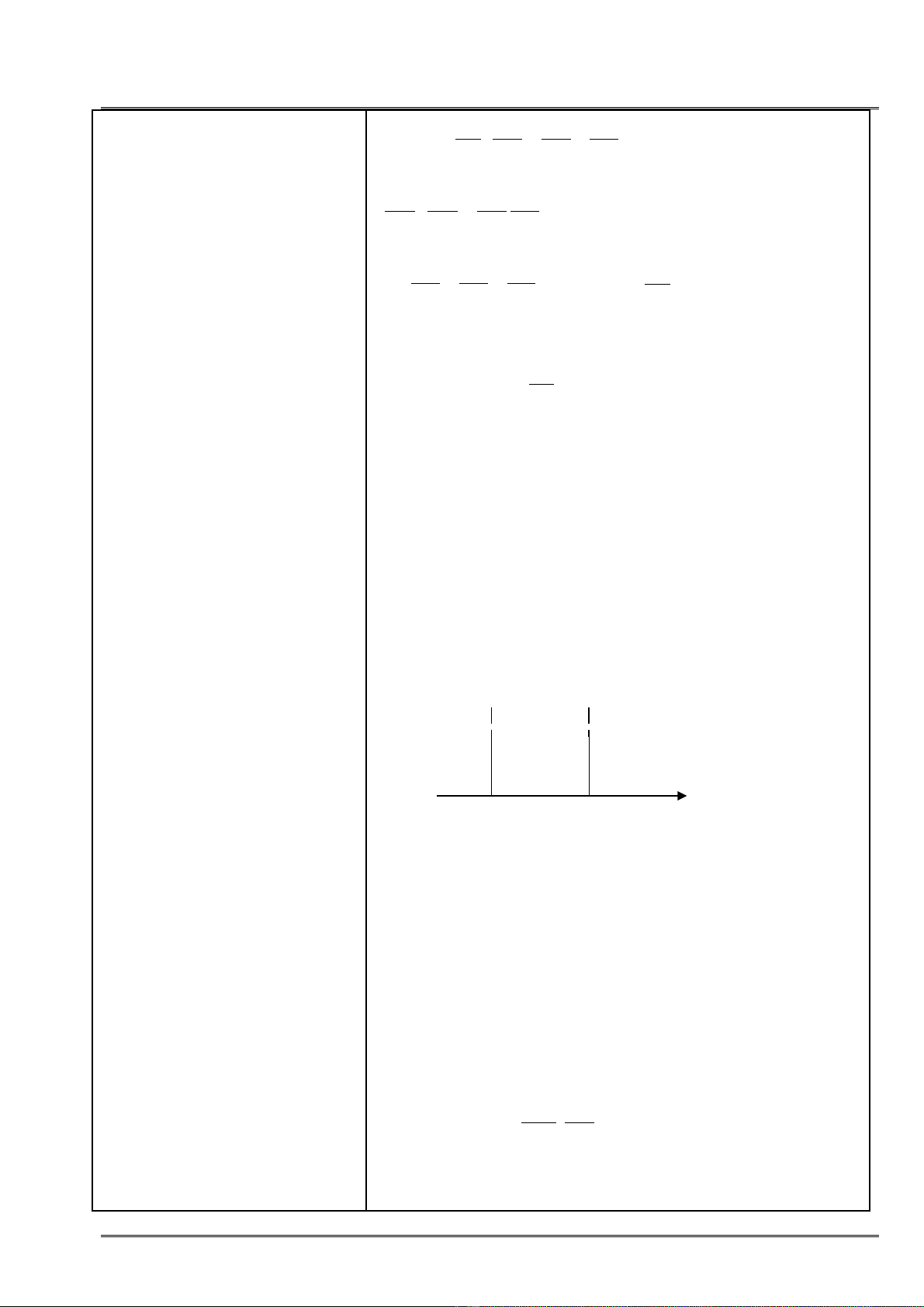
II. H t chuy n đ ng t do trong h p th ch nh tạ ể ộ ự ộ ế ữ ậ
m t chi uộ ề
-Xét h p th cao vô h n, b r ng c a h p th OA =ộ ế ạ ề ộ ủ ộ ế
L
-Ch n chi u sâu c a h p th là Ox -> hàm sóng s làọ ề ủ ộ ế ẽ
hàm c a bi n x : ủ ế
)(x
ψ
-> ph m vi h t chuy n đ ng : 0 < x < Lạ ạ ể ộ
Khi x = 0 =>
)(x
ψ
=
)0(
ψ
= 0
Khi x = L =>
)(x
ψ
=
)(L
ψ
= 0
-> Là hai đi u ki n biên c a bài toánề ệ ủ
Th năng U(x) = ế
≥≤∞
<<
Lxxkhi
Lxkhi
;0
00
Trong ph m vi h p th năng = 0ạ ộ ế
∧∧∧ += UTH
=
2
22
.
2dx
d
m
T−
=
∧
Ph ng trình Srođing :ươ ơ
Khoa T Nhiên – Tr ng Cao đ ng S ph m Qu ng Ninhự ườ ẳ ư ạ ả
x
O L