
quang
quang ®
®i
iÖ
Ön
nt
tö
öv
vμ
μ
th
th«
«ng
ng tin
tin quang
quang s
sî
îi
i
VLKT 2007

1.2 Linh kiÖn dÉn sãng quang, sù lan truyÒn cña ¸nh
s¸ng trong linh kiÖn dÉn sãng quang
1.2.1 HÖ sîi quang - M¹ch quang tÝch hîp vµ những ®Æc ®iÓm
¾Cuèi thËp kû 60, kh¸i niÖm “quang häc tÝch hîp” (integrated
optics) xuÊt hiÖn
¾Quang häc tÝch hîp lµ ph−¬ngph¸ptruyÒnvµxölÝtÝnhiÖu
b»ng tia s¸ng
¾Mét sè −u ®iÓm vµ nh−îc ®iÓm cña ph−¬ng ph¸p truyÒn dÉn
b»ng sîi quang so víi c¸c ph−¬ng ph¸p truyÒn dÉn truyÒn thèng:
−u ®iÓm:
-Tr¸nh®−îc sù giao thoa cña sãng ®iÖn tõ.
-Tr¸nh®−îc sù chËp m¹ch ®iÖn hay bÞ nèi ®Êt.
- An toµn trong truyÒn tin, tr¸nh ®−îc “nghe trém”
- Tæn hao nhá (cã thÓ ®¹t 0,2dB/ km).
- D¶i th«ng réng, kh¶ n¨ng phøc hîp cao.
-KÝchth−íc nhá, träng l−îng nhÑ.
- VËt liÖu rÎ, dåi dµo
Nh−îc ®iÓm: Kh«ng chuyÓn t¶i ®−îc n¨ng l−îng ®iÖn.
1
λ
2
λ
1
λ
2
λ
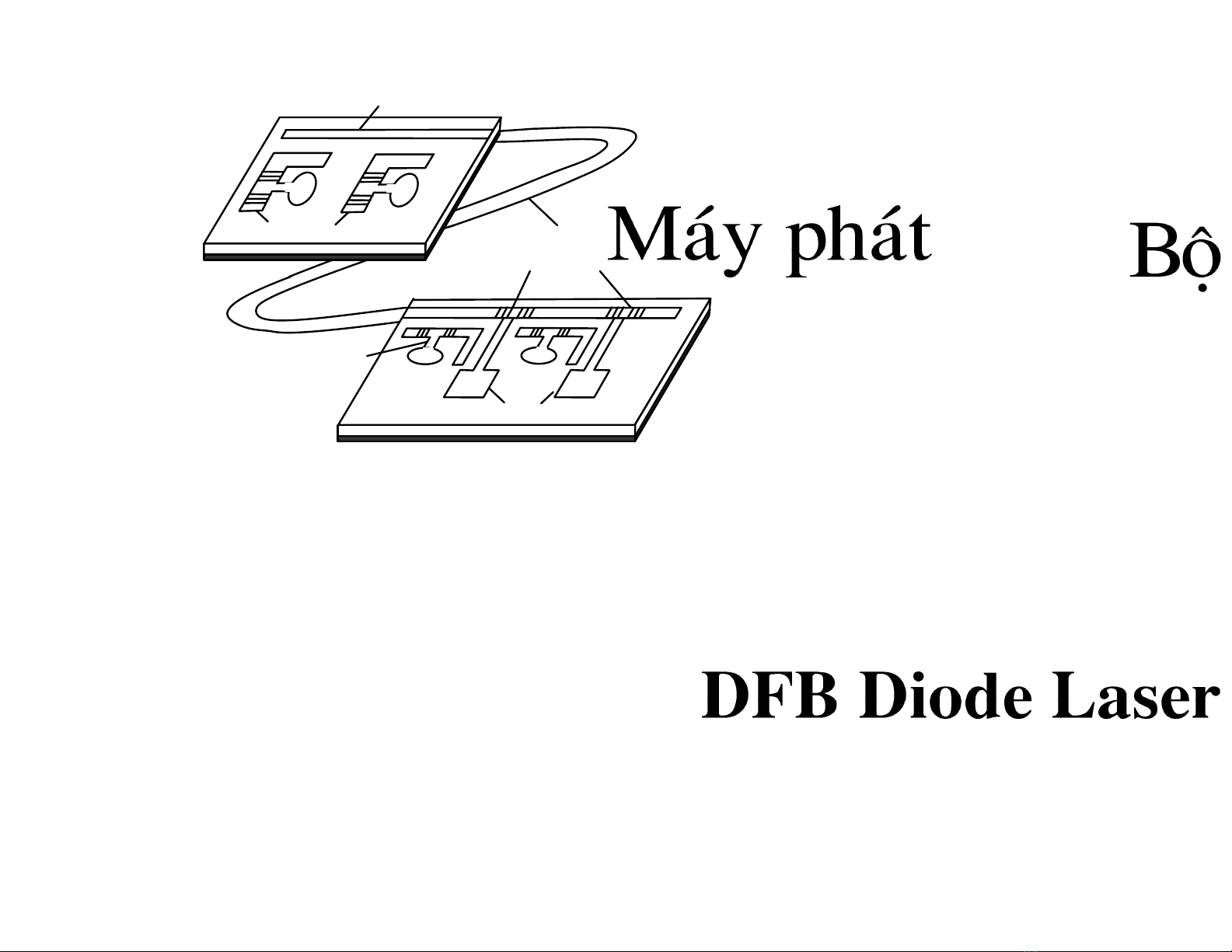
S¬ ®å hÖ sîi quang,
m¹ch quang tÝch hîp
D−u ®iÓm cña m¹ch quang tÝch hîp:
- T¨ng ®é réng d¶i th«ng.
- Më réng sù phøc hîp ph©n tÇn (frequency division
multiplexing).
- Khíp nèi Ýt tæn hao.
- Më réng chuyÓn m¹ch ®a cùc.
-KÝchth−íc nhá, träng l−îng nhÑ, c«ng suÊt tiªu thô Ýt.
- TiÕt kiÖm trong s¶n xuÊt.
- §é l¨p l¹i cao.
DNh−îc ®iÓm: CÇn ®Çu t− ®æi míi c«ng nghÖ cao tèn kÐm.
1.2.2 Ph−¬ng thøc truyÒn sãng (mode) trong linh kiÖn dÉn
sãng bản ph¼ng (lý thuyÕt quang sãng)
-Mode quang häc lµ c¸ch thøc ph©n bè theo kh«ng gian cña n¨ng
l−îng quang trong mét hay nhiÒu chiÒu to¹ ®é.
-VÒ to¸n häc mode lµ ®iÖn tr−êng thoảm·n ph−¬ng trình sãng
Maxwell víi những ®iÒu kiÖn biªn nhÊt ®Þnh
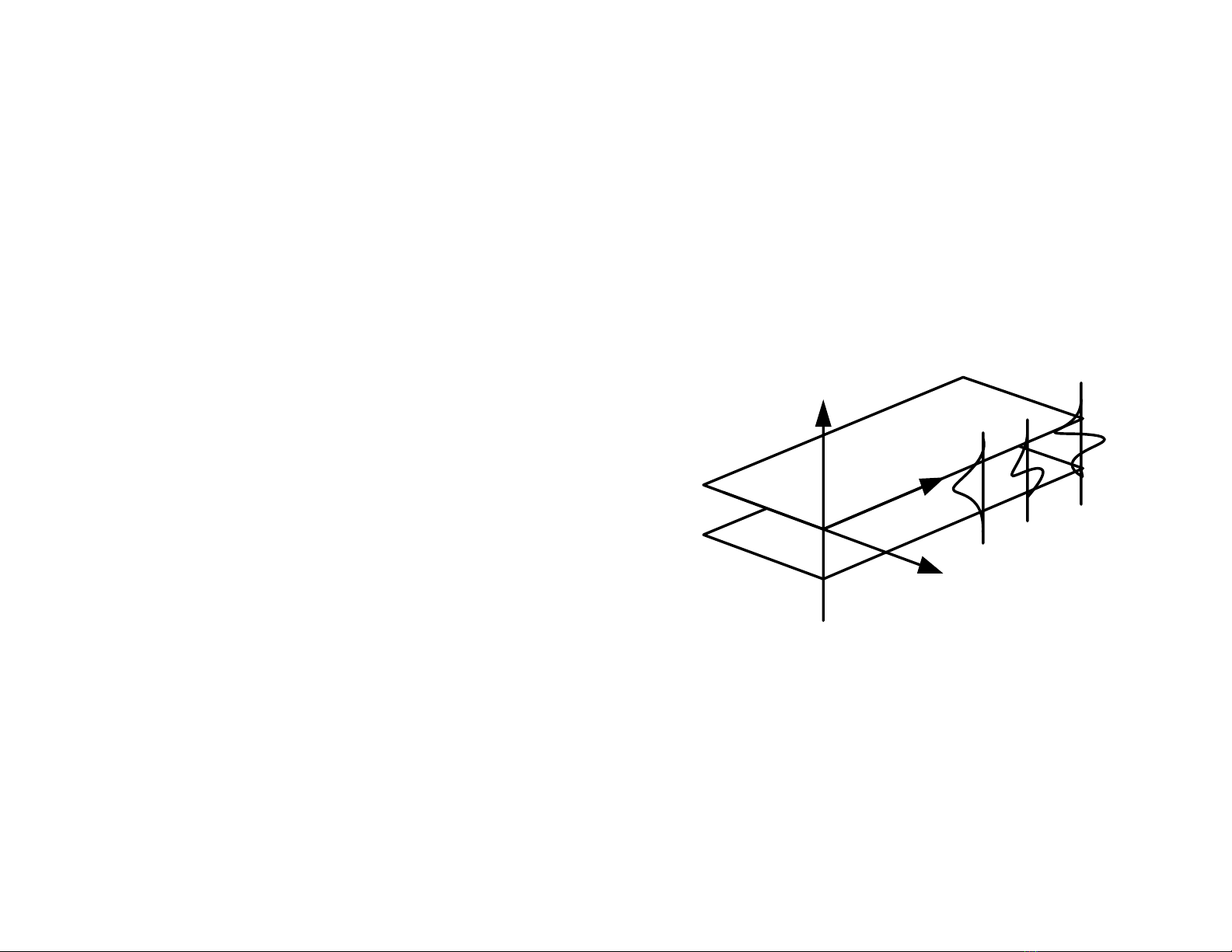
M« hình linh kiÖn dÉn sãng
bản ph¼ng
-Linh kiÖn dÉn sãng b¶n ph¼ng lµ
linh kiÖn dÉn sãng gồmbalípcãba
vïng chiÕt suÊt kh¸c nhau:
+Líp mét vµ ba lµ nöa v«
h¹n theo trôc x,
+Líp hai cã bÒ dµy giíi h¹n
theo trôc xlµ dg,
+Ba líp ®Òu v« h¹n theo hai
trôc yvµ z.

Ph−¬ng trình sãng Maxwell
() () ( ) ()
22
22
22
nr r,t
r,t ; n r
ct
∂
∇= =με
∂
ε
ε
G
G
GG
G
G
Tr−êng hîp sãng ®¬n s¾c
() ()
it
r,t r e
ω
=εε
GG
GG
() () ()
222
rknr r0∇+⋅ ⋅=εε
GGG
GG
GiảsösãnglantruyÒntheotrôcz
()
(
)
(
)
(
)
rx,y,zx,yexpiz== −βεε ε
G
GG G
Trong ®ã
β
lµ hÖ sè lan truyÒn
() () () ( )
22
22 2
22
x, y x, y kn r x, y 0
xy
∂∂⎡⎤
+
+−β =
⎢⎥
⎣⎦
∂∂
εε ε
G
GG
G
1
2
3
4
5







![Kiến thức về kết nối cáp quang [A-Z]](https://cdn.tailieu.vn/images/document/thumbnail/2011/20110102/linhsb/135x160/thao_luan_ve_ftth_7713.jpg)

![Hỏi đáp về cáp quang [mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2010/20100801/ht09dng/135x160/cap_quang_6552.jpg)











![Bài giảng Nhập môn Kỹ thuật điện [chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251208/nguyendoangiabao365@gmail.com/135x160/60591765176011.jpg)




