ĐH Công nghip Tp.HCM
dvntailieu.wordpress.com
Tuesday, December 07, 2010
Toán cao cp C2 Cao đng 1
TO
TOÁ
ÁN CAO C
N CAO C
P C2
P C2 CAO Đ
CAO Đ
NG
NG
PHÂN PH
PHÂN PH
I CHƯƠNG TRÌNH
I CHƯƠNG TRÌNH
S
S
ti
ti
t
t: 30
: 30
-----
-----
Chương 1. Hàm số nhiều biến số
Chương 2. Phương trình vi phân
Chương 3. Lý thuyết chuỗi
Chương 4. Một số bài toán kinh tế
Tài liệu tham khảo
1. Nguyễn Phú Vinh – Giáo trình Toán cao cấp
– ĐH Công nghiệp
TP. HCM.
Download Slide
Download Slide b
bà
ài
igi
gi
ng
ng To
Toá
án
n C
C2
2CĐ
CĐ t
t
i
i
dvntailieu.wordpress.com
dvntailieu.wordpress.com
Biên
Biên so
so
n
n:
:ThS
ThS.
. Đo
Đoà
àn
nVương
Vương Nguyên
Nguyên
2. Nguyễn Đình Trí
–
Toán cao cấp Tập 2
(dùng cho
SV Cao đẳng) –
NXB Giáo dục.
3. Lê Văn Hốt – Toán cao cấp C2
– ĐH Kinh tế
TP. HCM.
4. Đỗ Công Khanh – Toán cao cấp A3
–NXB
ĐHQG TP. HCM.
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
§1. Khái niệm cơ bản
§2. Đạo hàm riêng – Vi phân
§3. Cực trị của hàm hai biến số
……………………….
§1. KHÁI NIỆM CƠ BẢN
1.1. Các định nghĩa
a) Miền phẳng
• Trong mặt phẳng

, hình phẳng
giới hạn bởi các
đường cong kín được gọi là miền phẳng.
Tập hợp các đường cong kín giới hạn
được gọi là
biên của
, ký hiệu
∂
hay
Γ
.
Đặc biệt, mặt phẳng

được xem là miền p
hẳng với
biên ở vô cùng.
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
• Miền phẳng
kể cả biên
∂
được gọi là mi
ề
n
đ
óng
,
miền phẳng
không kể biên
∂
là mi
ề
n m
ở
.
• Miền phẳng
được gọi là mi
ề
n liên thông
nếu có 1
đường cong nằm trong
nối 2 điểm bất kỳ thuộc
.
Miền liên thông có biên là 1 đường cong kín được gọi
là miền đơn liên (hình a)
; có biên là nhiều đường cong
kín rời nhau là miền đa liên (hình b).
b) Lân cận của một điểm
• Khoảng cách giữa 2 điểm
,
là:
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
• Hình tròn
ε
mở có tâm
, bán kính
ε >
được
gọi là một lân cận của điểm
.
Nghĩa là:
∈ ε ⇔ − + − < ε
.
ε
(
)
(
)
(
)
= = − + −
.
c) Hàm số hai biến số
• Trong mặt phẳng

cho tập
⊂
ℝ
.
Tương ứng
→
ℝ
cho tương ứng mỗi
∈
với một giá trị
= ∈
ℝ
duy nhất
được gọi là
hàm số hai biến số
.
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
• Tập
⊂
ℝ
được gọi là miền xác định (MXĐ) của h
àm
số, ký hiệu
. Miền giá trị của hàm số là:
{
}
= = ∈ ∈ℝ
.
Chú ý
• Trong trường hợp xét hàm số
mà không nói gì
thêm thì ta hiểu MXĐ của hàm số là tập tất cả các điểm
∈
ℝ
sao cho
có nghĩa.
• Hàm có nhiều hơn hai biến được định nghĩa tương tự.
1.2.
Giới hạn của hàm số hai biến
s
ố
(
xem giáo trình
)
1.3. Hàm số liên tục (xem giáo trình)
ĐH Công nghip Tp.HCM
dvntailieu.wordpress.com
Tuesday, December 07, 2010
Toán cao cp C2 Cao đng 2
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
§2. ĐẠO HÀM RIÊNG – VI PHÂN
2.1. Đạo hàm riêng
a) Đạo hàm riêng cấp 1
• Cho hàm số
xác định trên miền mở
⊂
ℝ
chứa điểm
. Cố định
, nếu hàm số
có đạo hàm tại
thì ta gọi đạo hàm đó là
đạo hàm riêng
theo biến
của hàm số
tại
.
Ký hiệu:
hay
hay

∂
∂
Vậy

→
−
=
−
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
• Tương tự, đạo hàm riêng theo biến
tại
là:

→
−
=
−
Chú ý
• Nếu
là hàm số một biến
thì


∂
= =
∂
.
•
Hàm số nhiều hơn hai biến có định nghĩa t
ương tự
.
VD 1. Tính các đạo hàm riêng của hàm số:

= − + −
tại

−
.
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
VD 4. Tính các đạo hàm riêng của

=
.
b) Đạo hàm riêng cấp cao
• Đạo hàm riêng (nếu có) của hàm số
,
được gọi là các đạo hàm riêng cấp hai của
.
VD 3. Tính các đạo hàm riêng của

=
tại

π
.
VD 2. Tính các đạo hàm riêng của

+
=
+ +
.
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
Ký hiệu:
( )


∂ ∂ ∂
= = = =
∂ ∂
∂
,
(
)


∂ ∂ ∂
= = = =
∂ ∂
∂
,
( )

 
∂ ∂ ∂
= = = =
∂ ∂ ∂ ∂
,
(
)

 
∂ ∂ ∂
= = = =
∂ ∂ ∂ ∂
.
•
Hàm số nhiều hơn 2 biến và đạo hàm riêng cấp cao hơn
2 có định nghĩa t
ương tự
.
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
VD 6. Cho hàm số
= + −
.
Giá trị của đạo hàm riêng cấp năm

−
là:
A.


− =
; B.


− = −
;
C.


− =
; D.


− = −
.
VD 5. Tính các đạo hàm riêng cấp hai của hàm số:
= + −
tại

−
.
• Định lý Schwarz
Nếu hàm số
có các đạo hàm riêng
 
 
liên
tục trong miền mở
⊂
ℝ
thì
 
 
=
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
2.2. Vi phân
2.2.1. Vi phân cấp 1
a) Số gia của hàm số
• Cho hàm số
xác định trong lân cận
ε
của điểm
. Cho
một số gia
và
một
số gia
, khi đó hàm
có tương ứng số gia:

= + + −
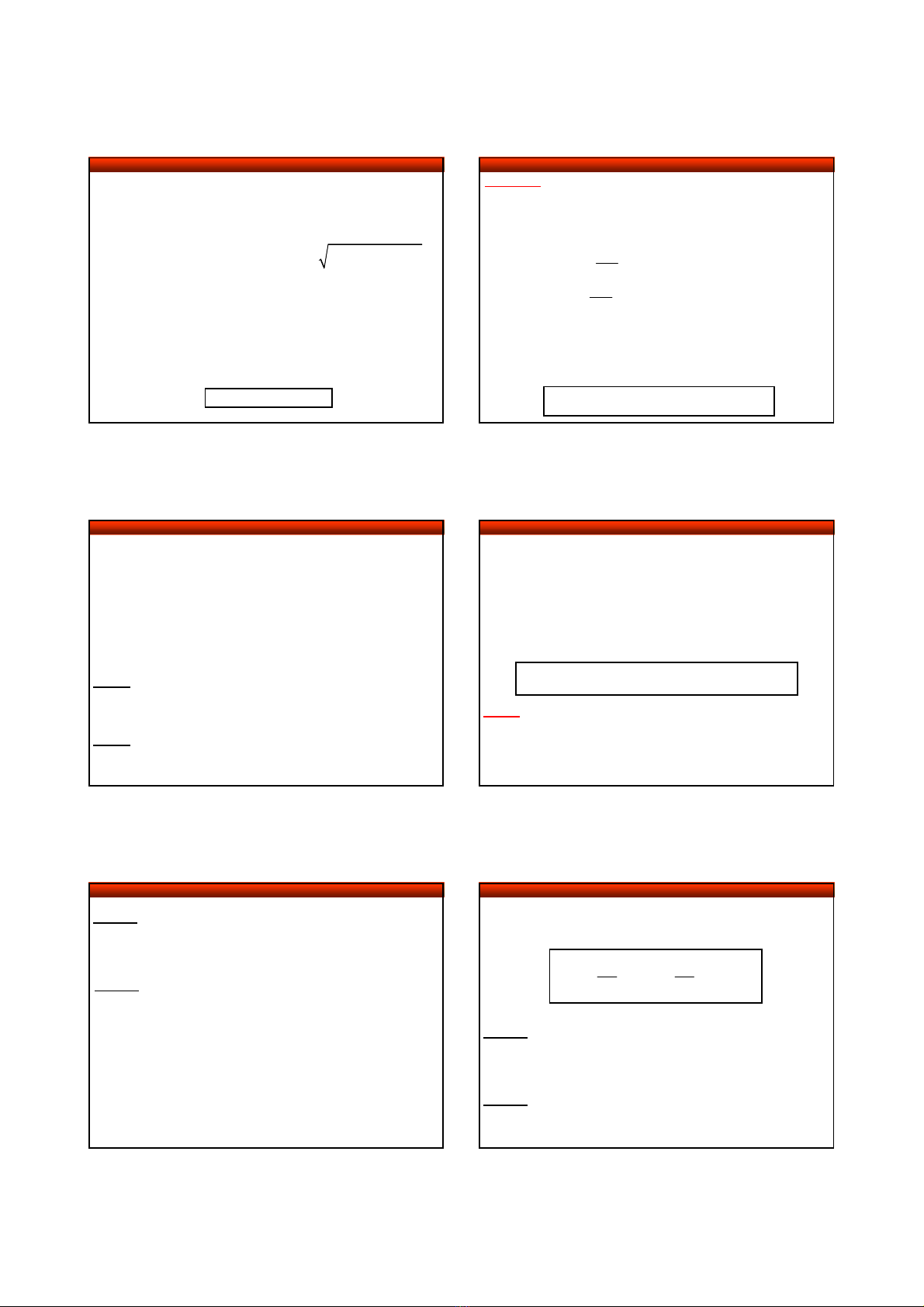
VD 7. Đạo hàm riêng

−
+
≥
của
−
=
là:
A.
+ −
−
; B.
+ −
−
;
C.
−
−
; D.
−
−
.
ĐH Công nghip Tp.HCM
dvntailieu.wordpress.com
Tuesday, December 07, 2010
Toán cao cp C2 Cao đng 3
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
b) Định nghĩa
• Nếu trong lân cận
ε
với số gia
,
mà số
gia
tương ứng có thể viết được dưới dạng
(
)
= + + = +
trong đó
là những số
chỉ phụ thuộc vào điểm
và hàm
, không phụ thuộc
thì đại lượng
+
được gọi là vi phân
của hàm
số
tại điểm
. Khi đó,
được
gọi là khả vi tại điểm
.
Ký hiệu

= +
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
Nhận xét
• Xét những điểm
+ +
dịch chuyển
trên đường đi qua
song song
. Khi đó
=
:
= + − = +

→
⇒ = ⇒ =
.
Tương tự,

→
= ⇒ =
.
Suy ra
= +
.
• Xét

= ⇒ = ⇒ =
.
Tương tự,

=
. Vậy:
 
= +
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
c) Định lý
• Nếu hàm số
có các đạo hàm riêng
trong lân cận
nào đó của
và các đạo hàm riêng này
liên tục
tại
thì
khả vi tại
.
VD 8. Cho hàm
−
= −
. Tính


−
.
VD 9. Tính vi phân cấp 1 của hàm


−
=
.
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
Ký hiệu và công thức:
(
)
 


   
= = + +
Chú ý
• Nếu
là các biến không độc lập (biến trung gian)
= ϕ ψ
,
= ϕ ψ
thì công
thức trên không còn
đúng nữa. Sau đây ta chỉ xét trường hợp
độc lập.
2.2.2. Vi phân cấp 2
• Giả sử
là hàm khả vi với
là các biến độc
lập. Các số gia
 
= =
tùy ý độc lập với
nên được xem là hằng số đối với
. Vi phân của

được gọi là vi phân cấp 2 của
.
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
VD 11. Tính vi phân cấp 2 của hàm


=
.
VD 10. Cho hàm số

= + −
.
Tính vi phân cấp hai


−
.
2.3. Đạo hàm của hàm số ẩn (hai biến)
• Hàm
xác định trên
⊂
ℝ
thỏa
phương trình
= ∀ ∈ ⊂
(*) được gọi là
hàm số ẩn
hai biến xác định bởi (*)
.
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
Giả sử các hàm trên đều khả vi, đạo hàm 2 vế (*) ta được:
+ = + =
.
Vậy
( )
= − = − ≠
VD 12. Cho hàm ẩn
thỏa phương trình:


= + +
. Tính
.
VD 13. Cho hàm ẩn
thỏa phương trình mặt cầu:
+ + − + − − =
. Tính
.
ĐH Công nghip Tp.HCM
dvntailieu.wordpress.com
Tuesday, December 07, 2010
Toán cao cp C2 Cao đng 4
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
§3. CỰC TRỊ CỦA HÀM HAI BIẾN SỐ
3.1. Định nghĩa
• Hàm số
=
đạt cực trị thực sự tại
nếu với mọi điểm
khá gần nhưng khác
thì
hiệu
= −
có dấu không đổi.
• Nếu
>
thì
là giá trị cực tiểu và
là
điểm cực tiểu của
=
.
• Nếu
<
thì
là giá trị cực đại và
là
điểm cực đại của
=
.
VD 1. Hàm số
= + − = − +
⇒ ≥ ∀ ∈
ℝ
nên đạt cực tiểu tại
.
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
3.2. Định lý
a) Điều kiện cần
• Nếu hàm số
=
đạt cực trị tại
và
tại đó hàm số có đạo hàm riêng thì:

= =
Điểm
thỏa
= =
được
gọi là điểm dừng,
có thể không là điểm cực trị.
b) Điều kiện đủ
Giả sử
=
có điểm dừng là
và có đạo hàm
riêng cấp hai tại lân cận của điểm
.
Đặt
 

 

= = =
.
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
Khi đó:
• Nếu

− >
⇒
>
đạt cực tiểu tại
.
• Nếu

− >
⇒
<
đạt cực đại tại
.
• Nếu

− < ⇒
không đạt cực trị tại
.
• Nếu

− =
thì
ta
không thể kết luận.
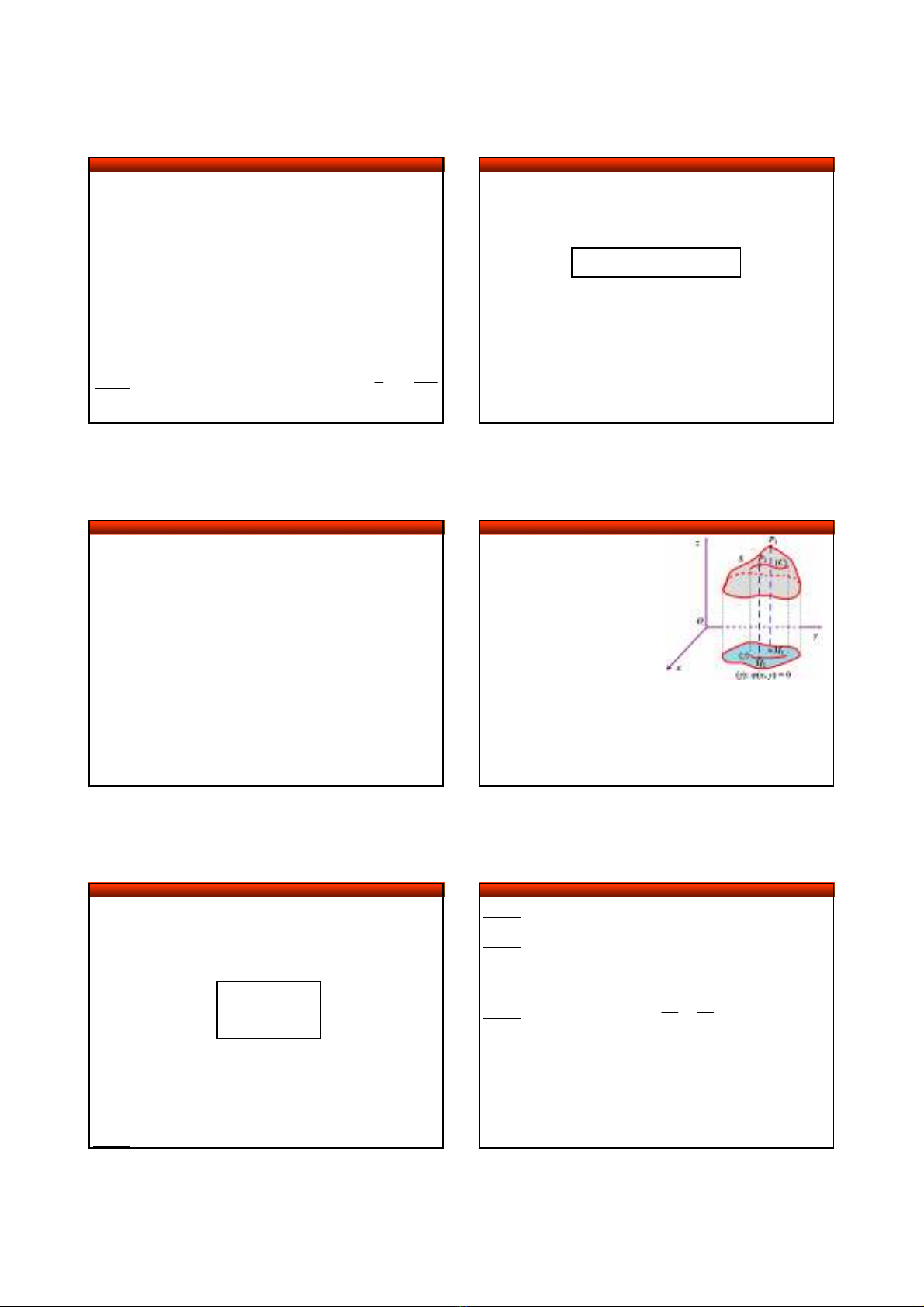
3.3. Phân loại cực trị
• Trong không gian

, xét mặt cong
chứa đường
cong
. Chiếu
lên mp

ta được miền
⊂
ℝ
và đường cong phẳng
γ ϕ =
(xem hình vẽ).
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
Khi đó, điểm
∈
là
điểm cao nhất (hay thấp
nhất) so với các điểm ở
trong lân cận của nó và
hình chiếu
∈
là
được gọi là điểm cực trị
tự do của hàm
xác định trên
(vì không phụ thuộc vào
γ
).
Tương
tự, điểm
∈
là điểm cao nhất (hay thấp nhất)
so
với các điểm ở trong lân cận của nó và hình chiếu
∈ γ
là điểm cực trị có điều kiện ràng buộc
bởi
γ ϕ =
của hàm
.
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
3.4. Cực trị tự do
Cho hàm số
xác định trên
. Để tìm cực trị (
tự
do) của
, ta thực hiện các bước sau:
• Bước 1. Tìm điểm dừng
bằng cách giải hệ:

=
=
• Bước 2. Tính




= =
,


= ⇒ = −
.
• Bước 3.
Dựa vào điều kiện đủ để kết luận.
VD 2. Tìm điểm dừng của hàm số

= − −
.
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
VD 3. Tìm cực trị của hàm

= + + − +
.
VD 4. Tìm cực trị của hàm số

= + − −
.
VD 5. Tìm cực trị của
= + − − +
.
VD 6. Cho hàm số
 


= + + > >
.
Khẳng định đúng là:
A.
đạt cực tiểu tại
 
và giá trị cực tiểu

=
.
B.
đạt cực tiểu tại
 
và giá trị cực tiểu

=
.
C.
đạt cực đại tại
 
và giá trị cực đại

=
.
D.
đạt cực đại tại
 
và giá trị cực đại

=
.
ĐH Công nghip Tp.HCM
dvntailieu.wordpress.com
Tuesday, December 07, 2010
Toán cao cp C2 Cao đng 5
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
• Để tìm cực trị có điều kiện của hàm số
ta dùng
phương pháp khử
hoặc
nhân tử Lagrange
.
a) Phương pháp khử
• Từ phương trình
ϕ =
ta rút
hoặc
thế vào
, sau đó tìm cực trị của hàm một biến.
3.5
. Cực trị có điều kiện
• Cho hàm số
xác định trên lân cận của điểm
thuộc đường cong
γ ϕ =
.
Nếu tại
hàm
đạt cực trị thì ta nói
là
điểm cực trị có điều kiện của
với điều kiện
ϕ =
.
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
VD 7. Tìm điểm cực trị của hàm
=
thỏa điều kiện:
− + =
.
b) Phương pháp nhân tử Lagrange
Tại điểm cực trị
của
, gọi
λ = − = −
ϕ ϕ
là
nhân tử Lagrange
.
Đ
ể
t
ìm
c
ự
c
t
r
ị
t
a
t
h
ự
c
h
i
ệ
n
c
ác
b
ư
ớ
c
:
• Bước 1. Lập hàm phụ (hàm Lagrange):

λ = + λϕ
• Bước 2. Giải hệ:
λ
= = =
⇒
điểm dừng
ứng với
λ
.
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
• Bước 3. Tính vi phân cấp 2 tại
ứng với
λ
:
 


  
= + +
Các vi phân
 
phụ thuộc vào điều kiện ràng buộc:

 
 
ϕ = ϕ + ϕ =
+ >
• Bước 4. Từ điều kiện ràng buộc (1) và (2), ta có:
Nếu
>
thì
đạt cực tiểu tại
.
Nếu
<
thì
đạt cực đại tại
.
Nếu
=
thì
không là điểm cực trị.
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
VD 8.
Tìm điểm cực trị của hàm số
= +
với điều kiện
+ =
.
VD 9. Tìm điểm cực trị của hàm

=
thỏa điều kiện
+ =
.
……………………………………….
Chương
Chương 2.
2. Phương
Phương tr
trì
ình
nh vi
vi phân
phân
§1. Phương trình vi phân cấp 1
§2. Phương trình vi phân cấp 2
……………………………
§1. PHƯƠNG TRÌNH VI PHÂN CẤP I
1.1. Khái niệm cơ bản về phương trình vi phân cấp 1
• Phương trình vi phân cấp 1 là phương trình có dạng
tổng quát
′
=
(*). Nếu từ (*) ta giải được
theo
′
thì (*) trở thành
′
=
.
• Nghiệm của (*) có dạng
=
chứa hằng số
được
gọi là nghiệm tổng quát. Khi thế điều kiện
=
cho trước (thường gọi là điều kiện đầu
) vào nghiệm
tổng quát ta được giá trị
cụ thể và nghiệm lúc này
được gọi là
nghiệm riêng
của (*).
Chương
Chương 2.
2. Phương
Phương tr
trì
ình
nh vi
vi phân
phân
VD 1. Cho phương trình vi phân
′
− =
(*).
Xét hàm số
= +
, ta có:
′
− =
thỏa phương trình (*).
Suy ra
= +
là nghiệm tổng quát của (*).
Thế
= =
vào
= +
, ta được:
= − ⇒ = −
là nghiệm riêng của (*) ứng với
điều kiện đầu

=
.