TÓM T T CÔNG TH C VÀ CÁC D NG TOÁN Đ C BI T Ắ Ứ Ạ Ặ Ệ V T LÍ 12Ậ
CH NG I: ƯƠ DAO Đ NG CỘ Ơ
I. DAO Đ NG ĐI U HOÀỘ Ề
1. Các ph ng trìnhươ
a. Ph ng trình dao đ ngươ ộ
x=Acos(ωt+ϕ ) (1)
x: to đ , v trí, li đ , đ d iạ ộ ị ộ ộ ờ
A: biên đ dao đ ng: giá tr c c đ i c a li đ A=xộ ộ ị ự ạ ủ ộ max
ω (rad/s): t n s góc; ầ ố ϕ (rad): pha ban đ u; (ầωt+ϕ ): pha c a dao đ ngủ ộ
xmax=A, xmin=−A, |x|min=0
b. V n t c trong dao đ ng đi u hòaậ ố ộ ề
v = x’
v= − ωAsin(ωt+ϕ) (2)
vmax=ωA, vmin=−ωA khi v t v trí cân b ng x=0ậ ở ị ằ
T c đố ộ: là đ l n c a v n t c |v|=ộ ớ ủ ậ ố
v
r
T c đ c c đ i |v|ố ộ ự ạ max=ωA khi v t v trí cân b ng (x=0).ậ ở ị ằ
T c đ c c ti u |v|ố ộ ự ể min=0 khi v t v trí biên (x=A ho c x = ậ ở ị ặ −A).
b. Gia t c trong dao đ ng đi u hòaố ộ ề
a=v’=x’’
a=−ω2Acos(ωt+ϕ ) (3)
a= − ω2x
Gia t c c c đ i aố ự ạ max = ω2A,
Gia t c c c ti u aố ự ể min= −ω2A.
Gia t c có đ l n c c đ i |a|ố ộ ớ ự ạ max = ω2A khi v t v trí biên (x=A ho c x = ậ ở ị ặ −A).
Gia t c có đ l n c c ti u |a|ố ộ ớ ự ể min=0 khi v t v trí cân b ng (x=0).ậ ở ị ằ
2. Chu kì, t n s , t n s gócầ ố ầ ố
Đ i v i con l c c a lò xoố ớ ắ ủ
ω=2πf , ω=2π/T,
m
k
=ω
;
0
g
l
ω
=∆
(4)
ω
π
=
2
T
;
k
m
2T
π=
;
1
Tf
=
(5)
m
k
2
1
fπ
=
;
π
ω
=2
f
;
1
fT
=
(6)
ω(rad/s); f (Hz); T(s); m(kg); k(N/m),
∆l0(m): đ dãn lò xo khi qu c u treo th ng đ ng cân b ngộ ả ầ ẳ ứ ằ
3. Năng l ng trong dao đ ng đi u hoàượ ộ ề
Đ ng năngộ
(7)
Th năngế
2
t
kx
W2
=
;
2 2
t
m x
W2
ω
=
(8)
C năng hay năng l ngơ ượ
W=Wđ+Wt ; (9)
2
kA
W2
=
;
2 2
m A
W2
ω
=
;
2
max
mv
W2
=
(10)
ThS. Liên Quang Th nh 0978 053 777. ịthinh1003@gmail.com. www.violet.vn/thinh1003/ -Page 1-
ThS. LIÊN QUANG TH NHỊ
Th c s v t líạ ỹ ậ
DĐ: 0978 053 777
E.mail: thinh1003@gmail.com
Website: violet.vn/thinh1003/
TÓM T T CÔNG TH C VÀ CÁC D NG TOÁN Đ C BI T Ắ Ứ Ạ Ặ Ệ V T LÍ 12Ậ
* Wđ=nWt ⇒
1
A
xn
=+
và
1
max
v n
vn
= +
* Wt=nWđ ⇒
và
1
max
v
vn
=+
Các đ n v : x(m); A(m); v(m/s); Wơ ị đ(J); Wt(J); W(J)
Dao đ ng đi u hoà có t n s góc là ộ ề ầ ố ω, t n s f, chu kỳ T. Thì đ ng năng và th năng bi n thiênầ ố ộ ế ế
v i cùng t n s góc 2ớ ầ ố ω, t n s 2f, chu kỳ T/2ầ ố
¯ Công th c liên hứ ệ gi a x, v, A và ữω đ c l p v i th i gian t ộ ậ ớ ờ
Ch ng minhứ:
TừW=Wđ+Wt ⇔
2
xm
2
mv
2
Am 22222 ω
+=
ω
⇔ ω2A2=v2+ω2x2 (11)
2 2
v A x
ω
= −
;
2
2
2
v
Ax ω
−±=
;
2
2
2
v
xA ω
+=
,
2 2
| v |
A x
ω = −
,
2 2
2
4 2
a v
A
ω ω
= +
,
2 2 2 2
21 2 2 1
2 2
1 2
v x v x
Av v
−
=−
,
2 2
21 2
2 2
2 1
v v
x x
ω
−
=−
(12)
CÁC D NG TOÁN Ạ
1. Các b c l p ph ng trình dao đ ng dao đ ng đi u hoà:ướ ậ ươ ộ ộ ề
* Tính ω
* Tính A
* Tính ϕ d a vào đi u ki n đ u: lúc t = tự ề ệ ầ 0 (th ng tườ 0 = 0)
0
0
Acos( )
sin( )
x t
v A t
ω ϕ
ω ω ϕ
= +
= − +
⇒
cos
sin
x
A
v
A
ϕϕ
ϕω
=
−
=
(1)
L u ýư: + Tr c khi tính ướ ϕ c n xác đ nh rõ ầ ị ϕ thu c góc ph n t th m y c a đ ng trònộ ầ ư ứ ấ ủ ườ
l ng giác (th ng l y -π < ượ ườ ấ ϕ ≤ π).
+ V t chuy n đ ng theo chi u d ng: v > 0 thì ch n ậ ể ộ ề ươ ọ ϕ < 0.
+ Ng c l i v t chuy n đ ng ng c chi u d ng: v < 0 thì ch n ượ ạ ậ ể ộ ượ ề ươ ọ ϕ > 0.
2. Chi u dài qu đ o là 2A: ề ỹ ạ
A2
=
Chieàudaøiquyõñaïo
(2)
3. Quãng đ ng điườ
Quãng đ ng đi trong 1 chu kỳ luôn là 4A: n u t=T thì S=4A.ườ ế (3)
Quãng đ ng đi trong 1/2 chu kỳ là 2A: n u t=T/2 thì S=2A.ườ ế (4)
Quãng đ ng đi trong l/4 chu kỳ khi v t đi t VTCB đ n v trí biên ho c ng c l i là A ườ ậ ừ ế ị ặ ượ ạ
4. Kho ng th i gian ng n nh t đ v t đi t v trí có li đ xả ờ ắ ấ ể ậ ừ ị ộ 1 đ n xế2
2 1
t
ϕ ϕ
ϕ
ω ω
−
∆
∆ = =
v i ớ
1
1
2
2
s
s
x
co A
x
co A
ϕ
ϕ
=
=
và (
1 2
0 ,
ϕ ϕ π
) (5)
ThS. Liên Quang Th nh 0978 053 777. ịthinh1003@gmail.com. www.violet.vn/thinh1003/ -Page 2-
A
−
O
A
2
A
/12T
/ 6T
3
2
A
/ 6T
/12T
/ 4T
2
2
A
A
−
O
A
2
A
/12T
/ 6T
/8T/8T
/ 4T
∆ϕ
1
M
,
1
M
A
A
−
2
M
,
2
M
1
x
2
x
∆ϕ
x
TÓM T T CÔNG TH C VÀ CÁC D NG TOÁN Đ C BI T Ắ Ứ Ạ Ặ Ệ V T LÍ 12Ậ
5. Quãng đ ng v t đi đ c t th i đi m tườ ậ ượ ừ ờ ể 1 đ n tế2.
Xác đ nh: ị
1 1 2 2
1 1 2 2
Acos( ) Acos( )
à
sin( ) sin( )
x t x t
v
v A t v A t
ω ϕ ω ϕ
ω ω ϕ ω ω ϕ
= + = +
� �
� �
= − + = − +
� �
V n t c ậ ố v1 và v2 ch c n xác đ nh d uỉ ầ ị ấ
Phân tích: t2 – t1 = nT/2 + ∆t (n ∈N; 0 ≤ ∆t < T/2) (6)
Quãng đ ng đi đ c trong th i gian nT/2 là Sườ ượ ờ 1 = 2nA, trong th i gian ờ∆t là S2.
Quãng đ ng t ng c ng là ườ ổ ộ S = S1 + S2 (7)
L u ý: ư+ Tính S2 b ng cách đ nh v trí xằ ị ị 1, x2 và chi u chuy n đ ng c a v t trên tr c Ox.ề ể ộ ủ ậ ụ
N u vế1.v2>0 thì S2=|x1 − x2|
Chú ý các kho ng th i gian đ t bi t T/4, T/6, T/8, T/12.ả ờ ặ ệ
+ Trong m t s tr ng h p có th gi i bài toán b ng cách s d ng m i liên h gi aộ ố ườ ợ ể ả ằ ử ụ ố ệ ữ
dao đ ng đi u hoà và chuy n đ ng tròn đ u s đ n gi n h n.ộ ề ể ộ ề ẽ ơ ả ơ
+ T c đ trung bình c a v t đi t th i đi m tố ộ ủ ậ ừ ờ ể 1 đ n tế2:
2 1
tb
S S
vt t t
= =
∆ −
(8)
V i S là quãng đ ng tính nh trên.ớ ườ ư
6. Tính quãng đ ng l n nh t và nh nh tườ ớ ấ ỏ ấ v t đi đ c trong kho ng th i gian ậ ượ ả ờ
0 < ∆t < T/2.
V t có v n t c l n nh t khi qua VTCB, nh nh t khi qua v trí biên nên trong cùng m t kho ngậ ậ ố ớ ấ ỏ ấ ị ộ ả
th i gian, quãng đ ng đi đ c càng l n khi v t càng g n VTCB và càng nh khi càng g n vờ ườ ượ ớ ậ ở ầ ỏ ầ ị
trí biên.
S d ng m i liên h gi a dao đ ng đi u hoà và chuy n đ ng tròn đ u.ử ụ ố ệ ữ ộ ề ể ườ ề
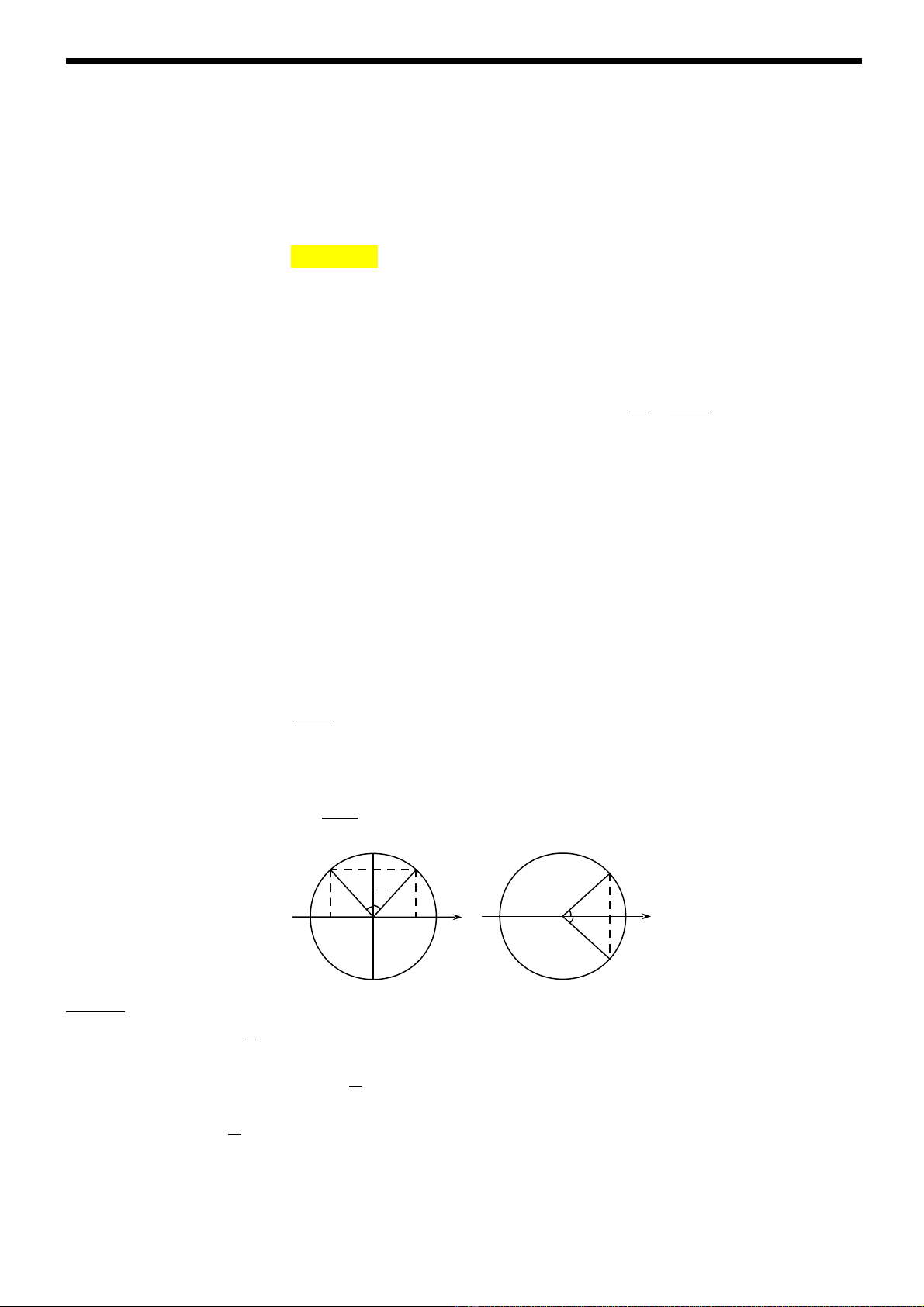
Góc quét ∆ϕ = ω∆t. (9)
Quãng đ ng l n nh t ng v i ch t đi m chuy n đ ng trên đ ng tròn đi t Mườ ớ ấ ứ ớ ấ ể ể ộ ườ ừ 1 đ n Mế2 đ iố
x ng qua tr c sin (hình 1), quãng đ ng là đo n Pứ ụ ườ ạ 1P2.
ax
.
2A sin 2
M
t
S
ω
∆
=
(10)
Quãng đ ng nh nh t ng v i ch t đi m chuy n đ ng trên đ ng tròn đi t Mườ ỏ ấ ứ ớ ấ ể ể ộ ườ ừ 1 đ n Mế2 đ iố
x ng qua tr c cos (hình 2), quãng đ ng đi đ c là 2 l n đo n PA.ứ ụ ườ ượ ầ ạ
.
2 (1 os )
2
Min
t
S A c
ω
∆
= −
(11)
L u ýư: + Trong tr ng h p ườ ợ ∆t > T/2
Tách
'
2
T
t n t∆ = + ∆
(12)
trong đó
*
;0 ' 2
T
n N t
< ∆ <�
Trong th i gian t=ờ
2
T
n
quãng đ ng luôn là S=n2Aườ (13)
Trong th i gian ờ∆t’ thì quãng đ ng l n nh t, nh nh t tính nh trên. ườ ớ ấ ỏ ấ ư
+ T c đ trung bình l n nh t và nh nh t c a trong kho ng th i gian ố ộ ớ ấ ỏ ấ ủ ả ờ ∆t:
ThS. Liên Quang Th nh 0978 053 777. ịthinh1003@gmail.com. www.violet.vn/thinh1003/ -Page 3-
-A A
M1
M2
P1
P2O
2
∆ϕ
M1
M2
PA
-A
O
/ 2
∆ϕ
TÓM T T CÔNG TH C VÀ CÁC D NG TOÁN Đ C BI T Ắ Ứ Ạ Ặ Ệ V T LÍ 12Ậ
ax
ax
M
tbM
S
vt
=∆
và
Min
tbMin
S
vt
=∆
(14)
v i SớMax; SMin tính nh trên.ư
7. Tính th i đi m v t đi qua v trí đã bi t xờ ể ậ ị ế (ho c v, a, Wặt, Wđ, F) l n th nầ ứ
* Gi i ph ng trình l ng giác l y các nghi m c a t (V i t > 0 ả ươ ượ ấ ệ ủ ớ ⇒ ph m vi giá tr c a k )ạ ị ủ
* Li t kê n nghi m đ u tiên (th ng n nh )ệ ệ ầ ườ ỏ
* Th i đi m th n chính là giá tr l n th nờ ể ứ ị ớ ứ
L u ýư: + Đ ra th ng cho giá tr n nh , còn n u n l n thì tìm quy lu t đ suy ra nghi m th nề ườ ị ỏ ế ớ ậ ể ệ ứ
+ Có th gi i bài toán b ng cách s d ng m i liên h gi a dao đ ng đi u hoà vàể ả ằ ử ụ ố ệ ữ ộ ề
chuy n đ ng tròn đ u: tìm th i gian tể ộ ề ờ 1 khi đ n l n th nh t, th hai tế ầ ứ ấ ứ 2 theo hình à tn l n th n. ầ ứ
8. Các b c gi i bài toán tìm s l n v t đi qua v trí đã bi t xướ ả ố ầ ậ ị ế (ho c v, a, Wặt, Wđ, F) t th iừ ờ
đi m tể1 đ n tế2.
* Gi i ph ng trình l ng giác đ c các nghi mả ươ ượ ượ ệ
* T từ1 < t ≤ t2 ⇒ Ph m vi giá tr c a (V i k ạ ị ủ ớ ∈ Z)
* T ng s giá tr c a k chính là s l n v t đi qua v trí đó.ổ ố ị ủ ố ầ ậ ị
L u ýư: + Có th gi i bài toán b ng cách s d ng m i liên h gi a dao đ ng đi u hoà vàể ả ằ ử ụ ố ệ ữ ộ ề
chuy n đ ng tròn đ u.ể ộ ề
+ Trong m i chu kỳ (m i dao đ ng) v t qua m i v trí biên 1 l n còn các v trí khác 2 l n.ỗ ỗ ộ ậ ỗ ị ầ ị ầ
9. Bài toán tìm li đ , v n t cộ ậ ố dao đ ng sau (tr c) th i đi m t m t kho ng th i gian ộ ướ ờ ể ộ ả ờ ∆t.
Bi t t i th i đi m t v t có li đ x = xế ạ ờ ể ậ ộ 0.
* T ph ng trình dao đ ng đi u hoà: x = Acos(ừ ươ ộ ề ωt + ϕ) cho x = x0
L y nghi m ấ ệ ωt +ϕ=α v i ớ
0
α π
(15)
ng v i x đang gi m (v t chuy n đ ng theo chi u âm vì v<0) ứ ớ ả ậ ể ộ ề
ho c ặωt + ϕ = −α (16)
ng v i x đang tăng (v t chuy n đ ng theo chi u d ng) ứ ớ ậ ể ộ ề ươ
* Li đ và v n t c dao đ ng sau (tr c) th i đi m đó ộ ậ ố ộ ướ ờ ể ∆t giây là
x Acos( )
Asin( )
t
v t
ω α
ω ω α
= ∆ +
= − ∆ +
ho c ặ
x Acos( )
Asin( )
t
v t
ω α
ω ω α
= ∆ −
= − ∆ −
(12)
10. Dao đ ng có ph ng trình đ c bi tộ ươ ặ ệ
a. Ph ng trình d ngươ ạ x = a ± Acos(ωt + ϕ) v i a = constớ(18)
Biên đ là A, t n s góc là ộ ầ ố ω, pha ban đ u ầϕ
x là to đ , xạ ộ 0 = Acos(ωt + ϕ) là li đ . ộ
To đ v trí cân b ng x = a, to đ v trí biên x = a ạ ộ ị ằ ạ ộ ị ± A
V n t c v = x’ = xậ ố 0’, gia t c a = v’ = x” = xố0”
H th c đ c l p: a = -ệ ứ ộ ậ ω2x0 ,
2 2 2
0
( )
v
A x
ω
= +
(19)
b. Ph ng trình d ngươ ạ x = a ± Acos2(ωt + ϕ) (20)
Ti n hành h b c ta đ c: biên đ A/2; t n s góc 2ế ạ ậ ượ ộ ầ ố ω, pha ban đ u 2ầϕ. (21)
11. Đ ng năng và th năng trung bình trong th i gian nT/2 ( nộ ế ờ ∈N*, T là chu kỳ dao đ ng) là: ộ
2 2
W 1
2 4 m A
ω
=
(22)
II. CON L C LÒ XOẮ
*L c kéo v hay l c h i ph c Fự ề ự ồ ụ
Đ c đi mặ ể : - Là l c gây dao đ ng cho v t. F luôn h ng v VTCB.ự ộ ậ ướ ề
- F bi n thiên đi u hoà cùng t n s v i li đ . F t l v i li đ x, t l v i gia t c a.ế ề ầ ố ớ ộ ỉ ệ ớ ộ ỉ ệ ớ ố
F = − kx = − mω2x (*)
L c h i ph c c c đ i:ự ồ ụ ự ạ Fmax = kA = mω2A t i các v trí biên x = ạ ị ±A; Fmin = 0 t i VTCB x=0.ạ
ThS. Liên Quang Th nh 0978 053 777. ịthinh1003@gmail.com. www.violet.vn/thinh1003/ -Page 4-
TÓM T T CÔNG TH C VÀ CÁC D NG TOÁN Đ C BI T Ắ Ứ Ạ Ặ Ệ V T LÍ 12Ậ
1. Đ l n l c đàn h iộ ớ ự ồ
Fđh=k∆l (1)
∆l=|l − l0| (2)
∆l(m): đ bi n d ng c a lò xo, đ nén, đ dãnộ ế ạ ủ ộ ộ
k(N/m): đ c ng c a lò xo; lộ ứ ủ 0: chi u dài t nhiên c a lò xo;ề ự ủ
l: chi u dài lò xo lúc ta kh o sát (th ng là lúc b bi n d ng); Fề ả ườ ị ế ạ đh(N): l c đàn h i.ự ồ
Chú ý: L c tác d ng lên giá đ ho c đi m treo lò xo là l c đàn h i.ự ụ ỡ ặ ể ự ồ
2. Con l c lò xo dao đ ng ngangắ ộ
Khi qu c u v trí có to đ x: ả ầ ở ị ạ ộ ∆l=|x|
Fđh=k|x| (3)
L c đàn h i l n nh t: khi ự ồ ớ ấ ∆lmax=|x|max=A, v t v trí biênậ ở ị
Fđh max=kA (4)
L c đàn h i nh nh tự ồ ỏ ấ : khi ∆lmin=|x|min=0, v t v trí cân b ngậ ở ị ằ
Fđh min=0 (5)
CON L C LÒ XO DAO Đ NG THEO PH NG TH NG Đ NGẮ Ộ ƯƠ Ẳ Ứ
3. Đ dãn c a lò xoộ ủ t i v trí cân b ng Oạ ị ằ
Tr ng l c ọ ự
P
cân b ng v i l c đàn h i ằ ớ ự ồ
0dh
F
: Fđh0 =P ⇔ k∆l0 = mg
⇔
0
mg
lk
∆ =
,
02
g
l∆ = ω
(6)
∆l0 : đ dãn c a lò xo t i v trí cân b ng O; m(kg), k(N/m).ộ ủ ạ ị ằ
4. L c đàn h i tác d ng lên qu c u khi qu c u có to đ xự ồ ụ ả ầ ả ầ ạ ộ
To đ x có th nh n giá tr d ng ho c âm. Tuy nhiên ta ch xét v trí c th c a qu c u là ạ ộ ể ậ ị ươ ặ ỉ ị ụ ể ủ ả ầ ở
trên hay d i v trí cân b ng và tr tuy t đ i c a x ( |x| )ở ướ ị ằ ị ệ ố ủ
a. N u qu c u phía trên v trí cân b ng: ế ả ầ ở ị ằ ∆l = |∆l0 −|x||
Fđh=k.|∆l0 −|x| | (7)
b. N u qu c u phía d i v trí cân b ng: ế ả ầ ở ướ ị ằ ∆l = |∆l0 +|x||
Fđh=k.|∆l0 +|x| | (8)
T ng quát:ổ
N u ch n chi u d ng h ng lên: ế ọ ề ươ ướ ∆l = |∆l0 − x|
Fđh=k.|∆l0 − x| (9)
N u ch n chi u d ng h ng xu ng: ế ọ ề ươ ướ ố ∆l = |∆l0 +x|
Fđh=k.|∆l0 + x| (10)
Chú ý: V i x là t a đ , là giá tr đ i s .ớ ọ ộ ị ạ ố
5. L c đàn h i l n nh t, nh nh tự ồ ớ ấ ỏ ấ
Ta gi s hai v trí biên c a qu c u là C và D ả ử ị ủ ả ầ
(biên đ A=OC=OD)ộ
a. L c đàn h i l n nh tự ồ ớ ấ khi qu c u v trí biên phía d i v tríả ầ ở ị ướ ị
cân b ng (t i D)ằ ạ
Fđh.max=k.(∆l0 +A) (11)
hay Fđh.max=mg +kA (12)
*L c đ y (l c nén) đàn h i c c đ i:ự ẩ ự ồ ự ạ lúc v t v trí cao nh tậ ở ị ấ
FNmax = k(A - ∆l0) (13)
b. N u A<ế∆l0, L c đàn h i nh nh t khi qu c u v trí biênự ồ ỏ ấ ả ầ ở ị
phía trên v trí cân b ng (t i C) (Hình 1)ị ằ ạ
Fđh.min=k.(∆l0 –A) (14)
c. N u A>ế∆l0 : L c đàn h i nh nh t khi qu c u v trí đi m Iự ồ ỏ ấ ả ầ ở ị ể
phía trên v trí cân b ng, mà t i I lò xo không b bi n d ng, ị ằ ạ ị ế ạ lúc đó
t a đ đi m I là xọ ộ ể I, v i |xớI|=∆l0;
ThS. Liên Quang Th nh 0978 053 777. ịthinh1003@gmail.com. www.violet.vn/thinh1003/ -Page 5-
O
I
QQ
I
D
C
∆l0A
A
O
Hình 2
O
O
I
QQ
C
D
I
∆l0A
A
Hình 1