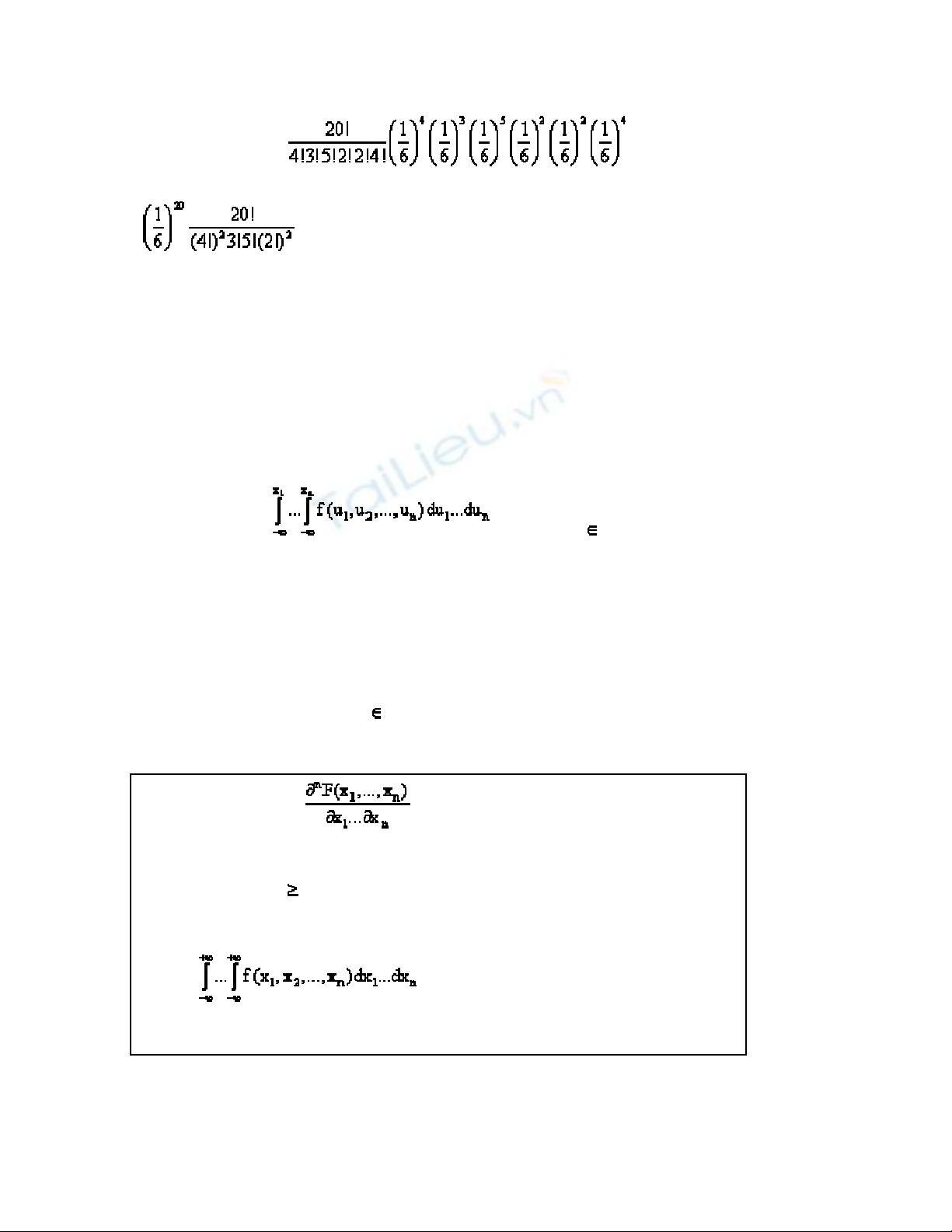
= =
3. Véc tơ ngẫu nhiên liên tục
Định nghĩa 3.1. Vectơ ngẫu nhiên n chiều X = (X1, X2,…, Xn) gọi là có phân phối
liên tục tuyệt đối nếu hàm phân phối đồng thời của nó có dạng:
F(x1,x2,…,xn) = ; (x1,…,xn) Rn
Hàm dưới dấu tích phân f(x1,..,xn) được gọi là hàm mật độ đồng thời của n biến
ngẫu nhiên X1,…,Xn.
Tính chất 3.2. Với (x1,…,xn) Rn
f(x1,…,xn) =
f(x1,…,xn) 0
= 1
Với D Ì R
n
thì
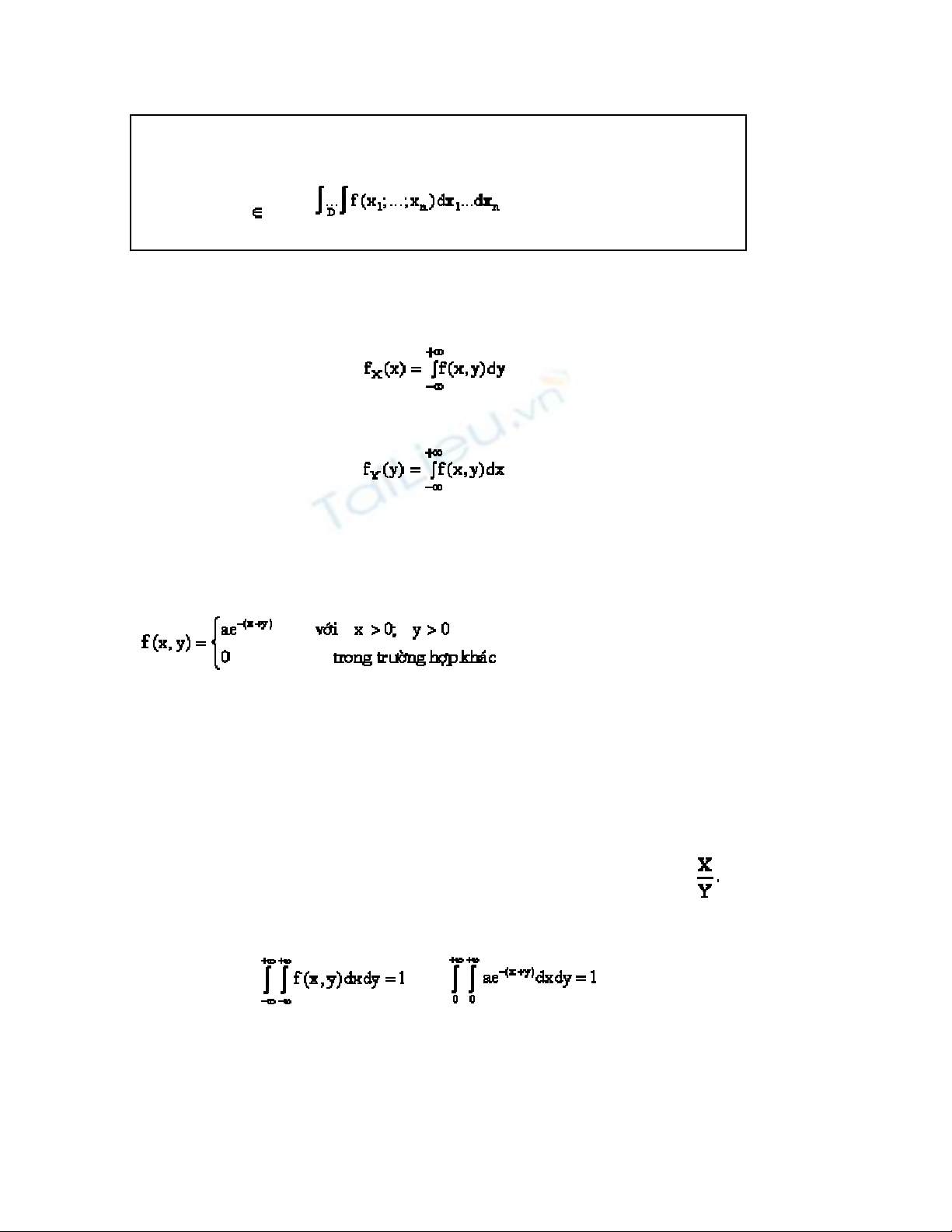
P[(X1,…,Xn) D] =
Trong trường hợp 2 chiều, nếu biết f(x, y) là hàm mật độ đồng thời của X và Y thì
Ø Hàm mật độ của X là
Ø Hàm mật độ của Y là
Ví dụ 3.3. Giả sử hai biến ngẫu nhiên X,Y có hàm mật độ đồng thời là
a- Tìm a và xác định hàm phân phối đồng thời của X và Y.
b- Xác định hàm mật độ của X; của Y.
c- Xác định hàm phân phối và hàm mật độ của biến ngẫu nhiên Z =
Giải. a- Ta có =>
<=> Û a.1 = 1. Vậy a = 1.
Hàm phân phối đồng thời của X, Y là
F(x,y) =
=
b- Hàm mật độ của X là
fX(x) = = =
Tương tự, hàm mật độ của Y là
fY(y) = = =
c- Với z > 0, hàm phân phối của Z là
Hàm mật độ của Z là
4. Sự độc lập của các biến ngẫu nhiên
Định nghĩa 4.1. Dãy n biến ngẫu nhiên X1,…,Xn, i = cùng xác định trên không
gian xác suất ( , ,P) được gọi là độc lập nếu
P
trong đó B1,B2,…,Bn B( R)
Dãy vô hạn các biến ngẫu nhiên X1,X2,…,Xn,… được gọi là độc lập nếu mọi dãy
con hữu hạn bất kì của dãy (Xn, n 1) là độc lập.
Định lí 4.2. Dãy n biến ngẫu nhiên X1, X2,..., Xn được gọi là độc lập khi và chỉ khi
F(x1, x2,...,xn) =
Định lí 4.3. Giả sử các biến ngẫu nhiên X1,..., Xn có hàm mật độ đồng thời
f(x1,...xn) và là hàm mật độ của từng biến Xi. Khi đó, điều kiện
cần và đủ để n biến ngẫu nhiên X1, X2,..., Xn độc lập là
f(x1, x2,...,xn) =
Định lí 4.4. Giả sử 1; 2 là hai hàm Borel và X, Y là các biến ngẫu nhiên độc
lập. Khi đó, các biến ngẫu nhiên Z1 = 1(X) và Z2 = 2(Y) cũng độc lập.
Ví dụ 4.5. Giả sử vectơ ngẫu nhiên (X, Y) có phân phối đều trên hình vuông
D = {(x, y) : 0 x 1; 0 y 1],
nghĩa là hàm mật độ của nó có dạng:
f(x, y) =
Chứng minh rằng X, Y là độc lập.
Giải. Hàm mật độ của X là
fX(x) = =
Tương tự,
fY(y) = =
Từ đó suy ra