
Nội dung
•Đồ thị và biểu diễn đồ thị
•Duyệt đồ thị
•Sắp xếp topo
•Tìm đường đi ngắn nhất

Đồ thị và biểu diễn đồ thị
Đồ thị
•Đồ thị G = (V, E) bao gồm một
tập đỉnh V và một tập cạnh E
•Mỗi cạnh là một cặp (v, w)
trong đó v, w V
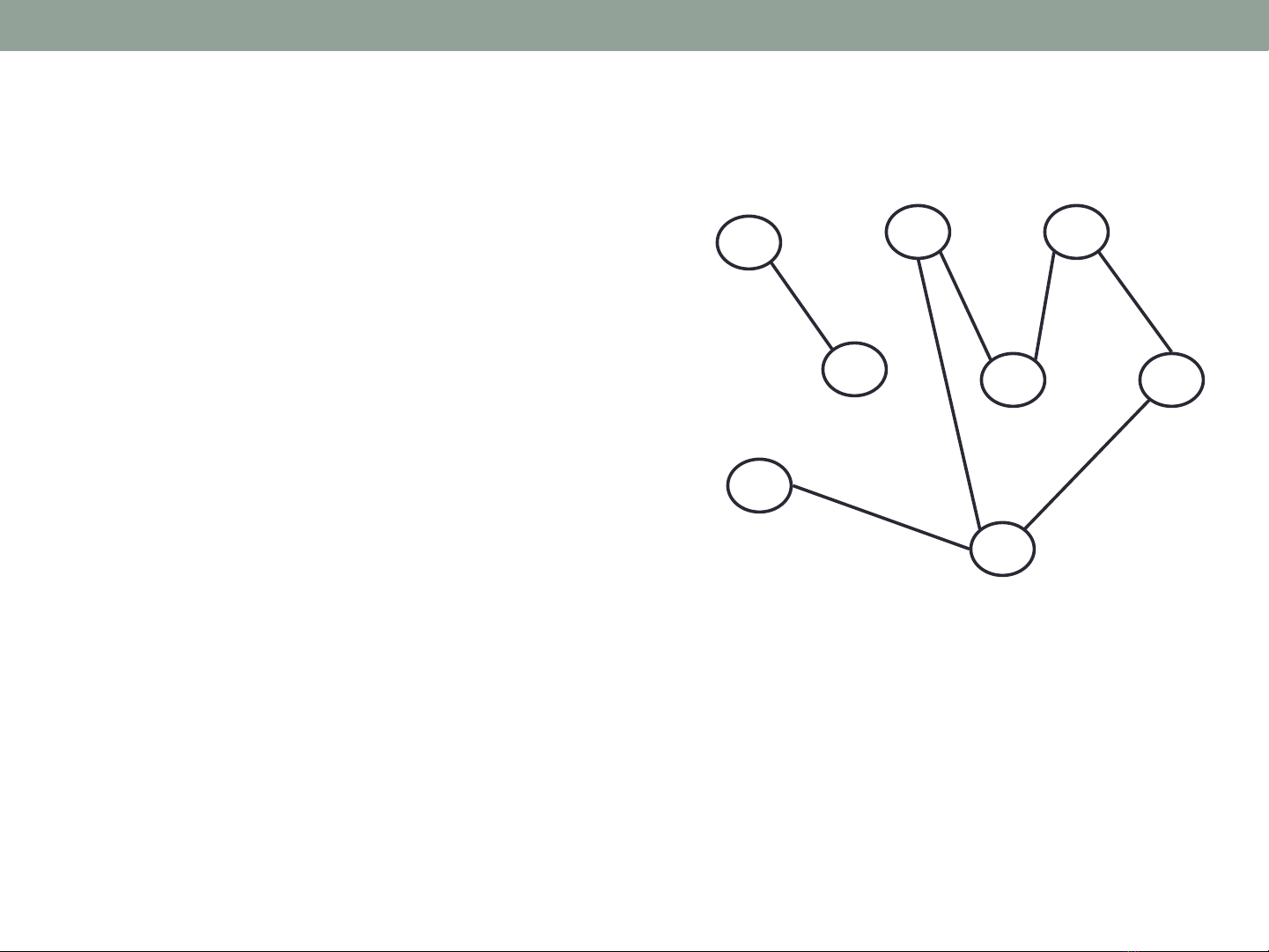
•Đồ thị không có hướng:
−Các cạnh không có thứ tự
−Cạnh (v, w) giống như cạnh (w, v)
•Đồ thị không có hướng được vẽ bằng
các nút cho các đỉnh và các đoạn thẳng
cho các cạnh
v1v2
v5
v7
v8
v3
v6
v4
Đồ thị có hướng
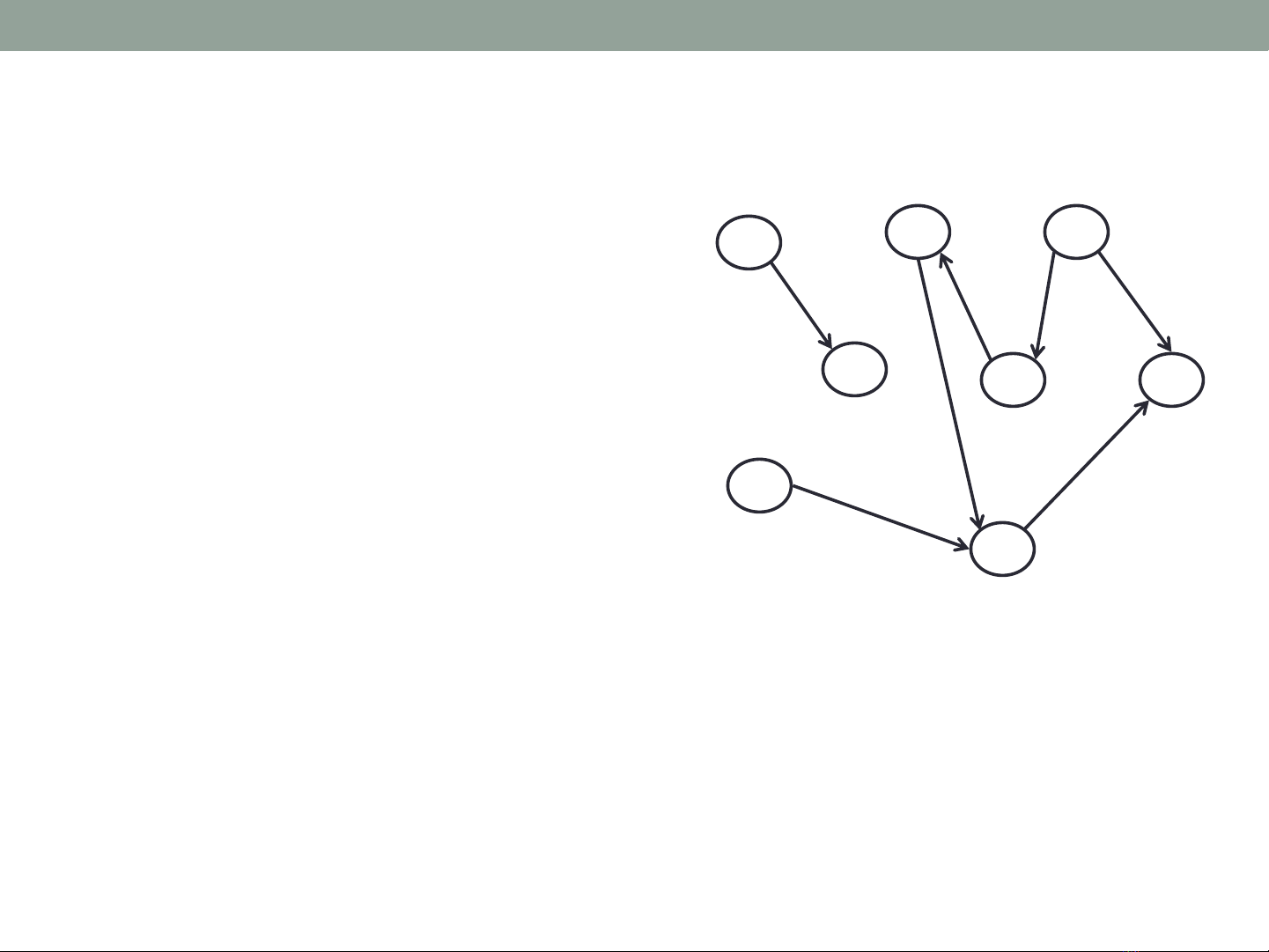
•Trong đồ thị có hướng, E là
một tập các cặp có thứ tự,
nhưng không nhất thiết là
tập đối xứng, tức là nếu cạnh
(v, w) có mặt thì cạnh (w, v)
có thể vắng mặt
•Đồ thị có hướng được vẽ bằng
các nút cho các đỉnh và các mũi
tên cho các cạnh
v1v2
v5
v7
v8
v3
v6
v4


![Bài giảng Thực hành cơ sở dữ liệu Trường ĐH Công Nghệ [năm] mới nhất](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251120/oursky02/135x160/14661768233842.jpg)
























