Một số khái niệm, điều kiện cân bằng pha, qui tắc pha Gibbs, giản đồ pha và các qui tắc pha là những nội dung chính trong bài giảng chương 4 "Lý thuyết cân bằng pha". Mời các bạn cùng tham khảo nội dung bài giảng để nắm bắt nội dung chi tiết.
AMBIENT/
Chủ đề:
Nội dung Text: Bài giảng Chương 4: Lý thuyết cân bằng pha
- CHƯƠNG 4
LÝ THUYẾT CÂN BẰNG PHA 4.1. Một số khái niệm
a. Pha
4.1. Một số khái niệm
• Pha là tập hợp những phần đồng
4.2. Điều kiện cân bằng pha thể của hệ, có cùng thành phần hóa
học và tính chất vật lý, hóa học ở
4.3. Qui tắc pha Gibbs mọi điểm, các pha được phân cách
nhau bởi bề mặt phân chia pha .
• Số pha được ký hiệu là f.
4.4. Giản đồ pha và các qui tắc pha
1 2
4.1. Một số khái niệm 4.1. Một số khái niệm
b. Hợp phần c. Số cấu tử
• Số cấu tử: là số hợp phần tối thiểu đủ để tạo nên hệ (xác
định trạng thái của hệ).
• Hợp phần:Là các chất( Đơn chất • Số cấu tử ký hiệu là k.( k ≤ r)
hoặc hợp chất) tạo thành hệ, mỗi • Hệ không có phản ứng hoá học: k = r
hợp phần đều có thể tách khỏi hệ và • Hệ có phản ứng hoá học: k < r
tồn tại độc lập ngoài hệ. • Có thể áp dụng quy tắc sau: k = r – q
Trong đó q là số phương trình liên hệ nồng độ giữa các cấu
• Số hợp phần: là tổng số các chất có tử và do điều kiện ban đầu quyết định. Số phương trình này
trong hệ, ký hiệu là r. phải độc lập với nhau.
3 4
1
- Ta có thể áp dụng công thức:
4.1. Một số khái niệm c = Σ (thông số trạng thái) - Σ (phương trình liên hệ)
d. Bậc tự do Ví dụ: Trạng thái của một khí lý tưởng được xác định bởi
3 thông số: T, P và V, nhưng giữa chúng lại có mối quan
hệ: PV = nRT
•Bậc tự do (hay độ tự do) của một nên bậc tự do: c = 3 -1 = 2
hệ là số thông số nhiệt động độc Hệ có c = 0 gọi là hệ vô biến tức là không có thông số
lập đủ để xác định hệ ở thời điểm trạng thái nào độc lập.
cân bằng. Hệ có c = 1 gọi là hệ nhất biến tức là chỉ có một thông số
trạng thái độc lập, các thông số khác là phụ thuộc.
•Ký hiệu bậc tự do là c.
Hệ có c = 2 gọi là hệ nhị biến có nghĩa là chỉ có hai thông
•Tổng quát: c ≥ 0 số trạng thái độc lập các thông số trạng thái khác là phụ
thuộc.
5 6
4.2. Điều kiện cân bằng pha 4.3. Qui tắc pha Gibbs
Các pha muốn tồn tại cân bằng với nhau thì Quy tắc pha Gibbs: C = k – f + n
với n là số thông số tác động lên hệ
phải có những điều kiện sau đây:
Thông thường 2 thông số đó là nhiệt độ và áp suất
Nhiệt độ của các pha phải như nhau. là hằng số nên : C = k – f + 2
β
Tα =T =...=T κ Nếu nhiệt độ là hằng số hoặc áp suất là hằng số thì:
Áp suất tác động các pha phải bằng nhau. C=k–f+1
β
Pα =P =...=P κ Qui tắc pha Gibbs là một trong những định luật tổng
Hoá thế của mỗi cấu tử trong các pha phải bằng quát nhất áp dụng cho mọi cân bằng pha, nó cho
μ α =μ β =...=μ κ
1 1 1
phép định tính mối quan hệ của những thông số
nhau μ α =μ
β
=...=μ κ
nhiệt động trong các quan hệ cân bằng dị thể và từ
2 2
----------
2
đó tìm ra các mối quan hệ định lượng giữa các
7 μ α =μ β =...=μ κ
8 thông số này.
k k k
2
- Bài tập ví dụ: 4.4. Giản đồ pha và các qui tắc pha
Ví dụ 1: Vận dụng quy tắc pha Gibbs, xác định số bậc tự do Giản đồ pha còn gọi là biểu đồ trạng thái là đồ thị mô tả sự phụ
thuộc giữa các thông số trạng thái của hệ nằm trong cân bằng pha.
của hệ gồm hỗn hợp NH4Cl, NH3 và HCl khi:
Một giản đồ pha bao gồm các đường, các mặt và các vùng.
– Nhiệt độ rất thấp. – Các đường dùng mô tả sự phụ thuộc giữa hai thông số,
– Nhiệt độ khá cao. – Các mặt trong không gian ba chiều mô tả sự phụ thuộc của ba thông số
nhiệt động
– Đun nóng.
– Các vùng trên giản đồ pha mô tả những hệ có số lượng và dạng các pha
xác định nằm cân bằng với nhau.
Ví dụ 2: Giải thích vì sao hệ KCl - NaCl - H2O là hệ 3 cấu tử
trong khi đó hệ KCl - NaBr - H2O lại là hệ 4 cấu tử. Giản đồ pha là công cụ đắc lực để nghiên cứu định tính cũng như
định lượng các quá trình chuyển pha, từ đó tính toán các thiết bị
trong dây chuyền công nghệ hóa học.
9 10
4.4.1. Cách biểu diễn các thông số nhiệt 4.4.1. Cách biểu diễn các thông số nhiệt
động trên giản đồ pha động trên giản đồ pha
a. Các thông số nhiệt độ, thể tích hay áp suất b. Biểu diễn thành phần của hệ 2 cấu tử
Trong hệ hai cấu tử, ta dùng một đoạn thẳng được chia thành
Đối với các thông số này ta dùng phương 100 phần như nhau.
pháp biểu diễn thông thường trên trục số.
Trong một số trường hợp, khi giá trị của
thông số thay đổi trong một khoảng khá rộng
thì có thể biểu diễn chúng dưới dạng nghịch Thành phần của các cấu tử trên giản đồ pha thường dùng là
đảo hay logarit của nó. phần mol xi, phần trăm khối lượng yi%( Hay % mol)
Biểu thức quan hệ: xA + xB = 1 hay y1 + y2 = 100%.
11 12 Khi điểm biểu diễn của hệ càng gần cấu tử nào thì hàm lượng
của cấu tử đó càng lớn.
3
- 4.4.1. Cách biểu diễn các thông số nhiệt 4.4.1. Cách biểu diễn các thông số nhiệt
động trên giản đồ pha động trên giản đồ pha
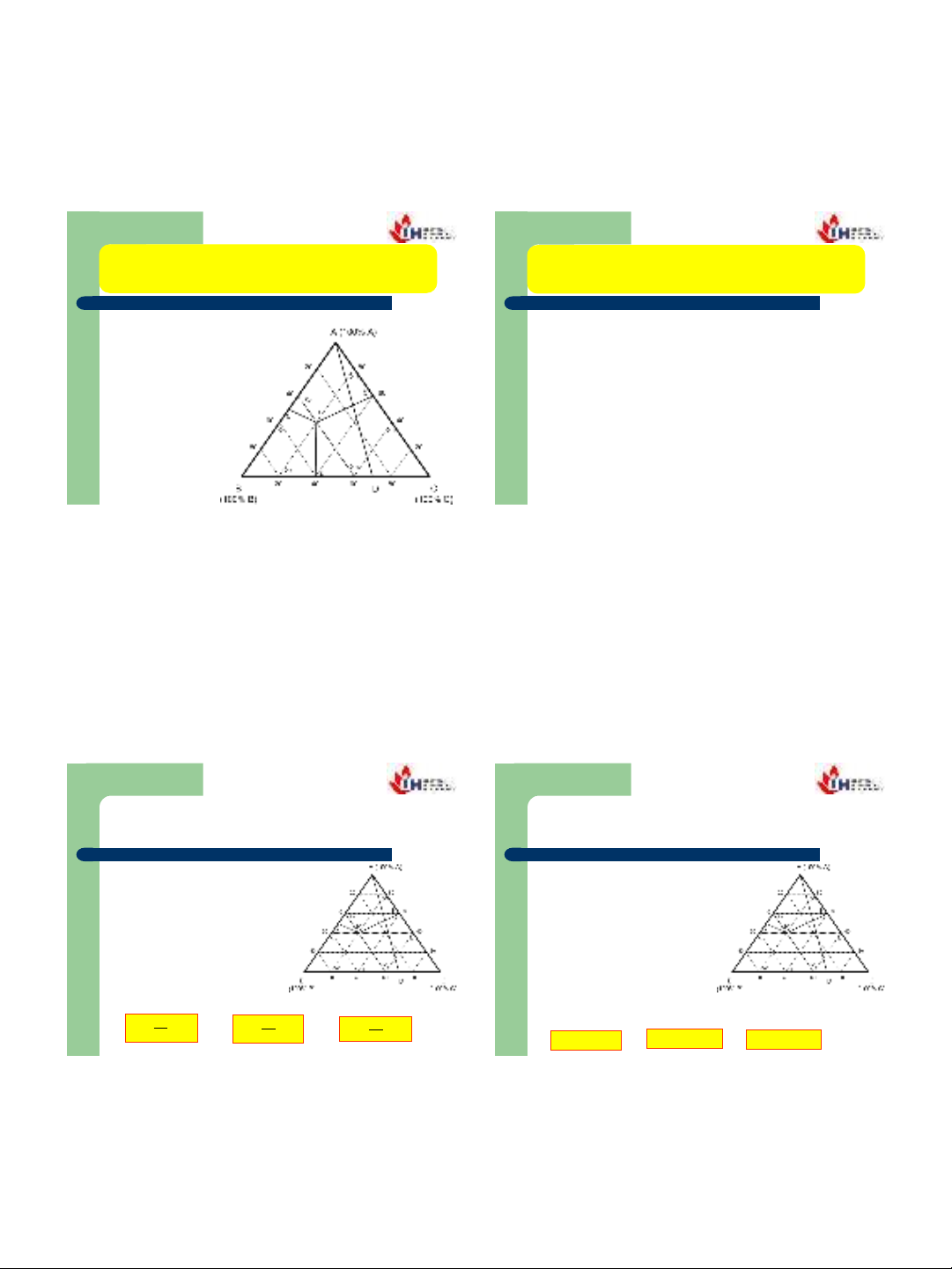
c. Biểu diễn thành phần của hệ 3 cấu tử c. Biểu diễn thành phần của hệ 3 cấu tử
Thành phần
Ba đỉnh của tam giác là ba điểm hệ của các cấu tử
của hệ 3 cấu nguyên chất A, B và C (100%).
tử thường Ba cạnh của tam giác AB, AC và BC biểu diễn thành
phần của hệ hai cấu tử.
được biểu Các điểm trong tam giác ABC biểu diễn thành phần
diễn bằng của hệ ba cấu tử.Thành phần mỗi cất tử được xác
định theo pp Gibbs hoặc Bozebom
một tam giác
13 đều : 14
c. Biểu diễn thành phần của hệ 3 cấu tử c. Biểu diễn thành phần của hệ 3 cấu tử
Phương pháp Gibbs: Phương pháp Bozebom:
Tổng các k/cách hạ từ 1 điểm bất kỳ trong tam giác Tổng độ dài các đoạn thẳng song song với các cạnh
xuống các cạnh bằng đường cao tam giác. xuất phát từ 1 điểm bất kỳ trong tam giác bằng cạnh
Thành phần của mỗi cấu tử được xác định bằng tỷ lệ tam giác.
của đoạn thẳng vuông góc hạ từ điểm biểu diễn Thành phần của hệ xác định bằng cách chiếu điểm
xuống cạnh đối diện của cấu tử đó với đường cao h. hệ song song với cạnh đối của đỉnh để biểu diễn
Ví dụ điểm P có thành phần ? thành phần của cấu tử đó.
Pa Pb Pc Ví dụ điểm P có:
%A 100%; %B 100% %C 100%
15 h h h
16 %A 40%; %B 40% %C 20%
4
- 4.4.2. Các quy tắc của giản đồ pha
c. Biểu diễn thành phần của hệ 3 cấu tử a. Quy tắc liên tục:
Với cách biểu diễn như trên, ta có nhận xét: Quy tắc: Các đường hoặc
Những điểm nằm trên cùng một đường thẳng song song các mặt trên giản đồ pha
với cạnh của tam giác thì tất cả điểm ấy đều có cùng
thành phần của cấu tử đối diện với cạnh đó. biểu diễn sự phụ thuộc
Những điểm nằm trên đường thẳng đi qua một đỉnh của giữa các thông số nhiệt
tam giác thì có cùng tỷ lệ thành phần của 2 cấu tử ứng
với hai đỉnh kia. động của hệ sẽ liên tục nếu
Khi tăng lượng tương đối của một cấu tử (ví dụ thêm cấu trong hệ không xảy ra sự
tử đó vào hệ) thì điểm hệ chung sẽ di chuyển trên đường
thẳng đi qua đỉnh biểu diễn cấu tử ấy và chạy về phía biến đổi chất, sự thay đổi
17 đỉnh. 18 số pha hoặc dạng các pha.
4.4.2. Các quy tắc của giản đồ pha 4.4.2. Các quy tắc của giản đồ pha
b. Quy tắc đường thẳng liên hợp c. Quy tắc đòn bẩy
Trong điều kiện đẳng nhiệt và đẳng áp, nếu hệ phân chia Nếu có ba hệ liên hợp H1, H2 và H thì lượng
thành hai hệ con (hay được tạo thành từ hai hệ con) thì điểm tương đối của chúng được tính theo quy tắc đòn
biểu diễn của ba hệ này phải nằm trên cùng một đường thẳng,
bẩy như sau:
đường thẳng này gọi là đường thẳng liên hợp.
19 20
5
- 4.4.2. Các quy tắc của giản đồ pha
d. Qui tắc khối tâm Bài tập:
Đây là trường hợp mở rộng của qui tắc đòn bẩy. Ví dụ 3: Cho hệ H, H1, H2 như hình vẽ, hệ H có
Nếu một hệ gồm n hệ con thì điểm biểu diễn của nó phải khối lượng 100g. Tính thành phần và khối lượng
nằm ở khối tâm vật lý của đa giác có đỉnh là các điểm của từng hệ.
biểu diễn của n hệ con.
Ví dụ: Hệ H gồm ba hệ con là H1, H2 và H3
Hệ K = hệ H1 + hệ H2
g1 H2K
g2 H1K
Hệ H = hệ K + hệ H3
gK g1 g2 HH3
21 g3 g3 KH 22
Bài tập 1: Bài tập 2:
Một hệ H gồm 3 cấu tử A, B và C có khối lượng
Một hỗn hợp 40% phenol trong nước phân thành
là 100g. Hệ H được phân thành 3 pha có các thành
hai lớp. Lớp thứ nhất chứa 70% phenol và 30%
phần tương ứng như sau:
nước, lớp thứ hai chứa 3% phenol và 97%
nước. Xác định khối lượng mỗi lớp, nếu lượng %A %B %C
hỗn hợp tổng cộng là 1kg. Hệ H 40 20 40
Pha H1 70 10 20
Pha H2 20 60 20
Pha H3 20 20 60
23 24 Hãy tính khối lượng của từng pha (hệ con).
6
Thêm vào BST
Báo xấu
Download
Vui lòng tải xuống để xem tài liệu đầy đủ
