
Ch ng 5ươ
H i qui v i bi n giồ ớ ế ả
I. B n ch t c a bi n gi - Mô hình ả ấ ủ ế ả
trong đó các bi n đ c l p đ u là ế ộ ậ ề
bi n giế ả
Bi n đ nh tính th ng bi u th các ế ị ườ ể ị
m c đ khác nhau c a m t tiêu th c ứ ộ ủ ộ ứ
thu c tính nào đó.ộ
Đ l ng hoá đ c bi n đ nh tính, ể ượ ượ ế ị
trong phân tích h i qui ng i ta s ồ ườ ử
d ng k thu t bi n gi .ụ ỹ ậ ế ả

Ví d 1ụ : M t cty s d ng 2 công ngh ộ ử ụ ệ
(CN) s n xu t (A, B). Năng su t c a m i ả ấ ấ ủ ỗ
CN là ĐLNN phân ph i chu n có ph ng ố ẩ ươ
sai b ng nhau, kỳ v ng khác nhau. MH ằ ọ
th hi n qh gi a năng su t c a cty v i ể ệ ệ ữ ấ ủ ớ
vi c s d ng CN s n xu t là :ệ ử ụ ả ấ
Yi = β1+ β2Zi + Ui
Trong đó : Y : năng su t, Z : bi n giấ ế ả
Zi = 1 n u s d ng CN Aế ử ụ
0 n u s d ng CN Bế ử ụ

Ta có :
E(Yi/Zi= 0) = β1 : năng su t trung ấ
bình c a CN B.ủ
E(Yi/Zi= 1) = β1+ β2 : năng su t trung ấ
bình c a CN A.ủ
⇒ β2: chênh l ch năng su t gi a CN A và ệ ấ ữ
CN B.
Gi thi t Hả ế 0 : β2 = 0 (⇔ gi a CN A và CN Bữ
không có khác bi tệv năng su t).ề ấ
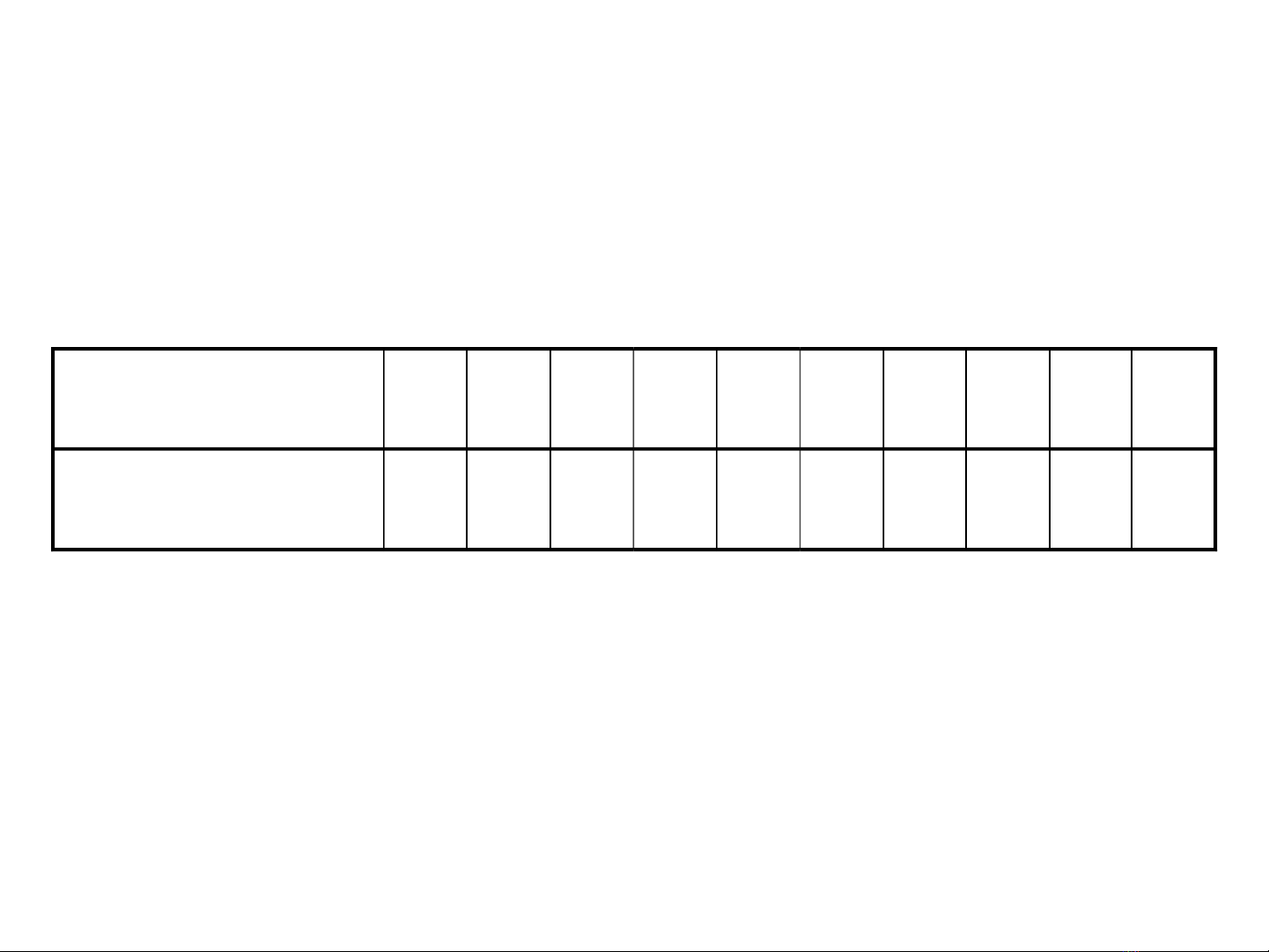
* Gi s ti n hành kh o sát năng su t ả ử ế ả ấ
c a CN A và CN B trong vòng 10 ủ
ngày, ng i ta thu đ c s li u sau :ườ ượ ố ệ
Năng su t (đvt : T n/ ngày)ấ ấ
Dùng m u s li u trên, h i qui mô hình ẫ ố ệ ồ
đang xét, ta có :
CN s d ngử ụ B A A B B A B A A B
Năng su t ấ28 32 35 27 25 37 29 34 33 30
ii
Z4,68,27Y
ˆ+=

Mô hình : Yi = β1+ β2Z1i + β3Z2i + Ui
Trong đó : Y - năng su t, Zấ1, Z2 : bi n giế ả
Z1i = 1 : s d ng CN Aử ụ
0 : không s d ng CN Aử ụ
Z2i = 1 : s d ng CN Bử ụ
0 : không s d ng CN Bử ụ
Ví d 2ụ : T ng t ví d 1, nh ng công ươ ự ụ ư
ty có 3 CN s n su t (A, B, C).ả ấ


























