Chương 4
TÍNH ỔN ĐỊNH CỦA HỆTHỐNG ĐIỀU KHIỂN
TỰ ĐỘNG PHI TUYẾN
4.1. KHÁI NIỆM VỀTÍNH ỔN ĐỊNH CỦA HỆ
THỐNG ĐIỀU KHIỂN TỰ ĐỘNG PHI TUYẾN
Nếu trạng thái của HTĐKTĐ phi tuyến được mô
tảbằng bằng hệ n phương trình vi phân:
nit
yyyfy nii ÷== 1
;
),,...,( 21
&
(4.1)
trong đó tham sốt chỉra rằng tác động bên ngoài
của HT thay đổi theo thời gian, thì nghiệm của
nó hoàn toàn được xác định bằng điều kiện ban
đầu y
i0
. Nghiệm này được gọi là chuyển động
“không bịnhiễu loạn”. Sự thay đổi ĐKBĐ đi một
giá trị
∆
y
i0
dẫn đến sự thay đổi nghiệm. Sai lệch
của nghiệm đó so với nghiệm không nhiễu loạn
gọi là chuyển động nhiễu loạn.
Hệ phương trình (4.1) khi tính đến sự thay đổi
ĐKBĐ có dạng:
.
),,...,(
2211
t
yyyyyyfyy
nniii
∆
∆
∆
∆
+++=+
&&
Có thểbiến đổi hệ phương trình trên vềdạng:
.
),,...,( 21 t
yyy
F
yn
i
i
∆
∆
∆
∆
=
&
(4.2)
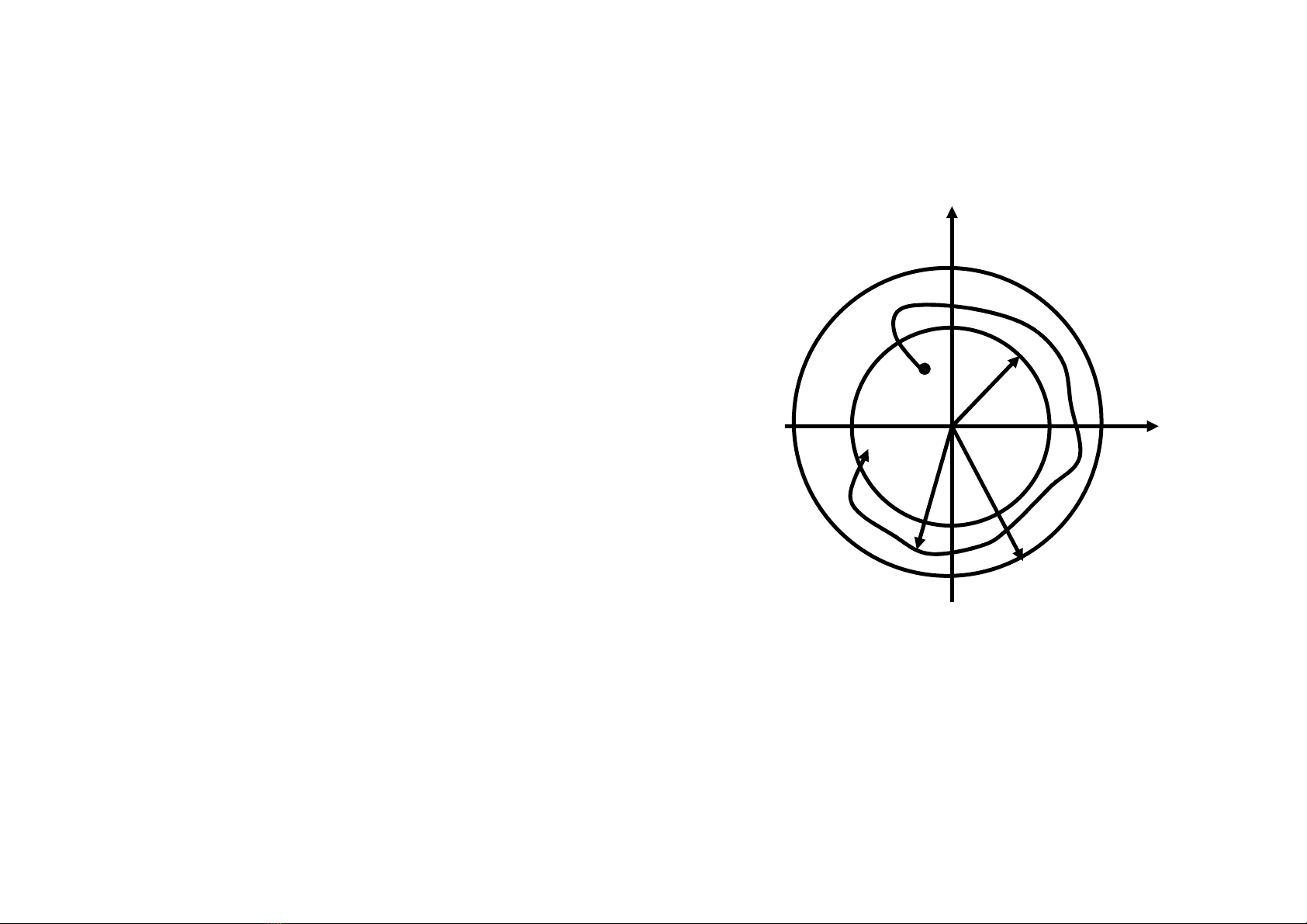
Xét quỹ đạo pha của HT khi không có tác động
bên ngoài:
∑∆
=
=
n
ii
y
R
1
2
2
Tại thời điểm ban đầu:
∑∆
=
=
n
ii
y
R
1
2
0
2
0
µ
R
0
ε
R
∆
y
1
∆
y
2
H.4-1
Khái niệm ổn định
Lyapunôp: chuyển động
không bịnhiễu sẽ ổn định
nếu với mọi
ε
(H.4-1) dương
nhỏbao nhiêu tùy ý, ta cũng
có thểchọn được một số
µ
sao cho với mọi
∆
y
i0
ban đầu thỏa mãn điều kiện
R
0
<
µ
thì sai lệch
∆
y
i
thỏa mãn bất đẳng thức
0
R<
ε
với mọi 0
≤
t
≤ ∞
. Nếu R
→
0 khi t
→ ∞
thì
chuyển động không bịnhiễu sẽ ổn định tiệm cận.
Còn nếu như không thểtìm được
µ
=
µ
(
ε
) để R<
ε
với mọi 0
≤
t
≤ ∞
thì chuyển động không bịnhiễu
sẽkhông ổn định.
Nếu như các điều kiện ổn định của HT chỉ được
thực hiện bắt đầu từcác giá trị
ε<ε
tới hạn
, tức là
chỉtrong một dải xác định các ĐKBĐ thì ta nói
rằng HT ổn định trong phạm vi nhỏ. Khi không có
hạn chếtrên thì HT ổn định trong phạm vi lớn
hay ổn định tiệm cận toàn bộ.
4.2 TIÊU CHUẨN ỔN ĐỊNH LYAPUNỐP
(SV tựnghiên cứu)