1
Chương 1 1
1. Các hệtoạđộ
2. Các yếutốvi phân
3. Phép tính vector
4. Tích phân
5. Các toán tử
CHƯƠNG 1: GIẢI TÍCH VECTOR
7:43 AM
7:43 AM Chương 1 2
Các hệtoạđộ
HệtoạđộDescartes
z
x
y
O
z
x
y
2
7:43 AM Chương 1 3
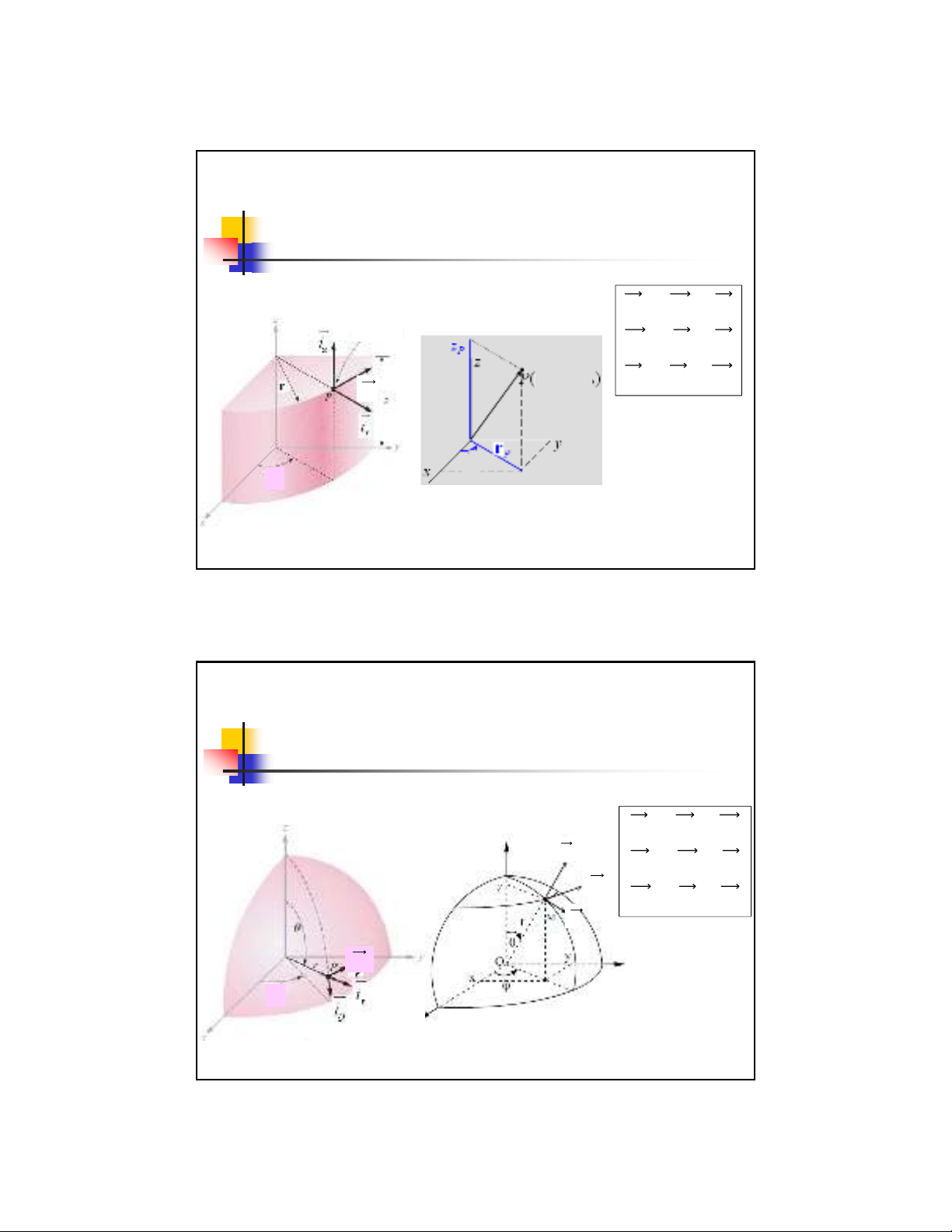
Các hệtoạđộ
Hệtoạđộtrụ
r,,z
rP,P,zP
P
7:43 AM Chương 1 4
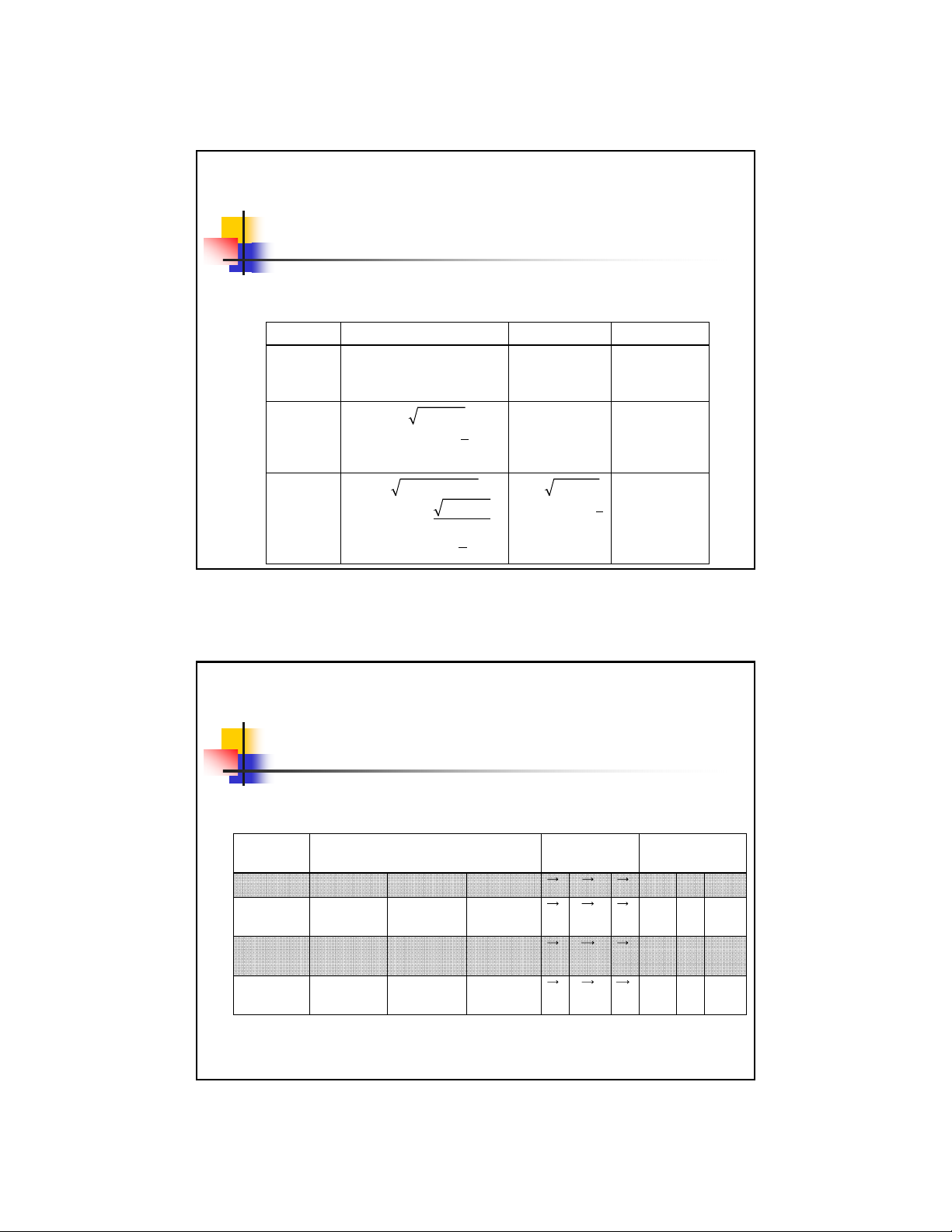
Các hệtoạđộ
Hệtoạđộcầu
3
7:43 AM Chương 1 5
Các hệtoạđộ
Liên hệgiữacáchệtoạđộ
Descartes TrụCầu
Descartes
(x,y,z) x = rcos
y = rsin
z = z
x = rsincos
y = rsinsin
z = rcos
Trụ
(r,,z)
z = z
r = rsin
=
z = rcos
Cầu
(r,,)
=
7:43 AM Chương 1 6
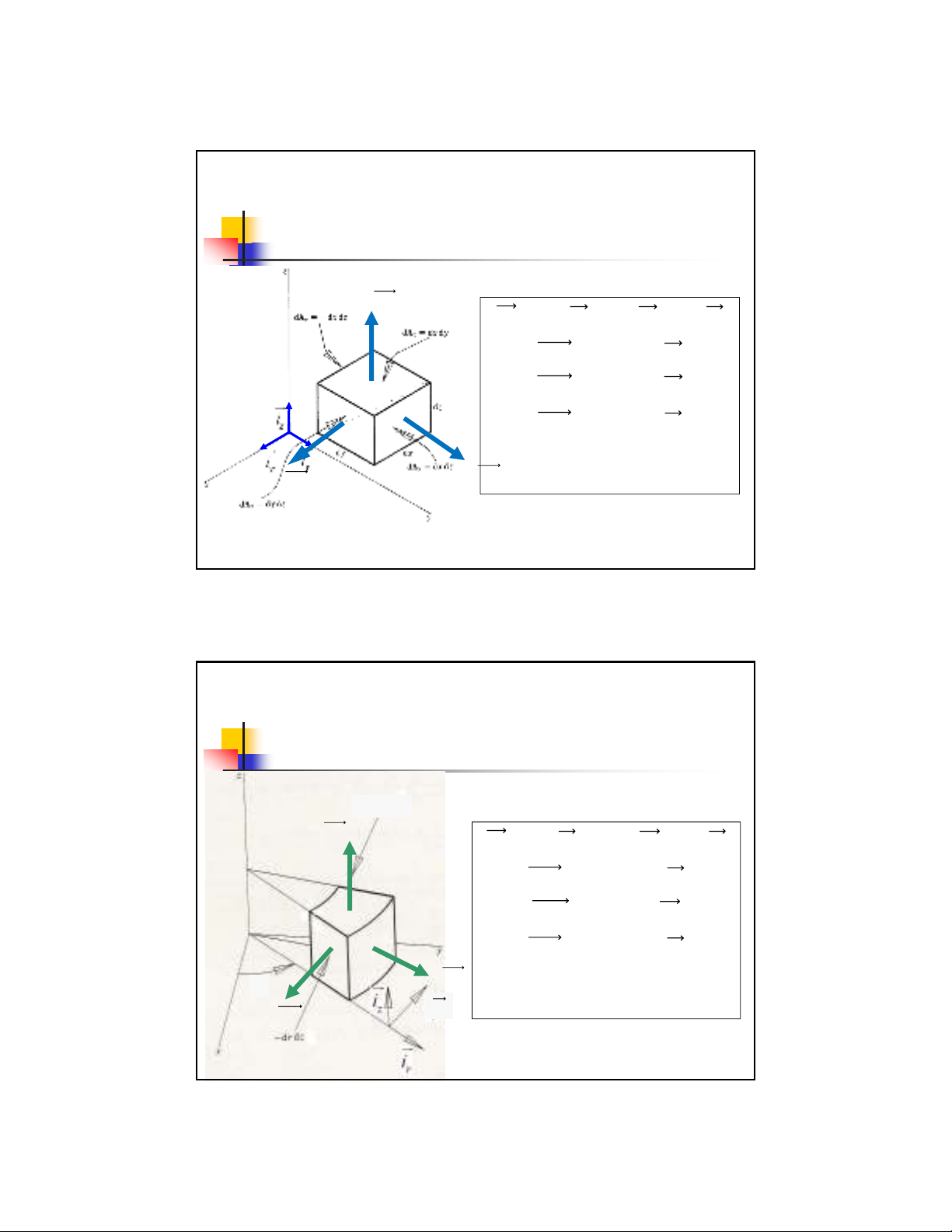
Các hệtoạđộ
Liên hệgiữacáchệtoạđộ
Toạđộ Vector đơn
vị
HệsốLarmor
u1u2u3h1h2h3
Descartes
(x,y,z) -< x <-< y <-< z <11 1
Trụ
(r,,z) 0r <0<2-< z <1r 1
Cầu
(r,,)0r <0<0<21r
rsin
4
7:43 AM Chương 1 7
Các yếutốvi phân
HệtoạđộDescartes
7:43 AM Chương 1 8
Các yếutốvi phân
Hệtoạđộtrụ
rdrd
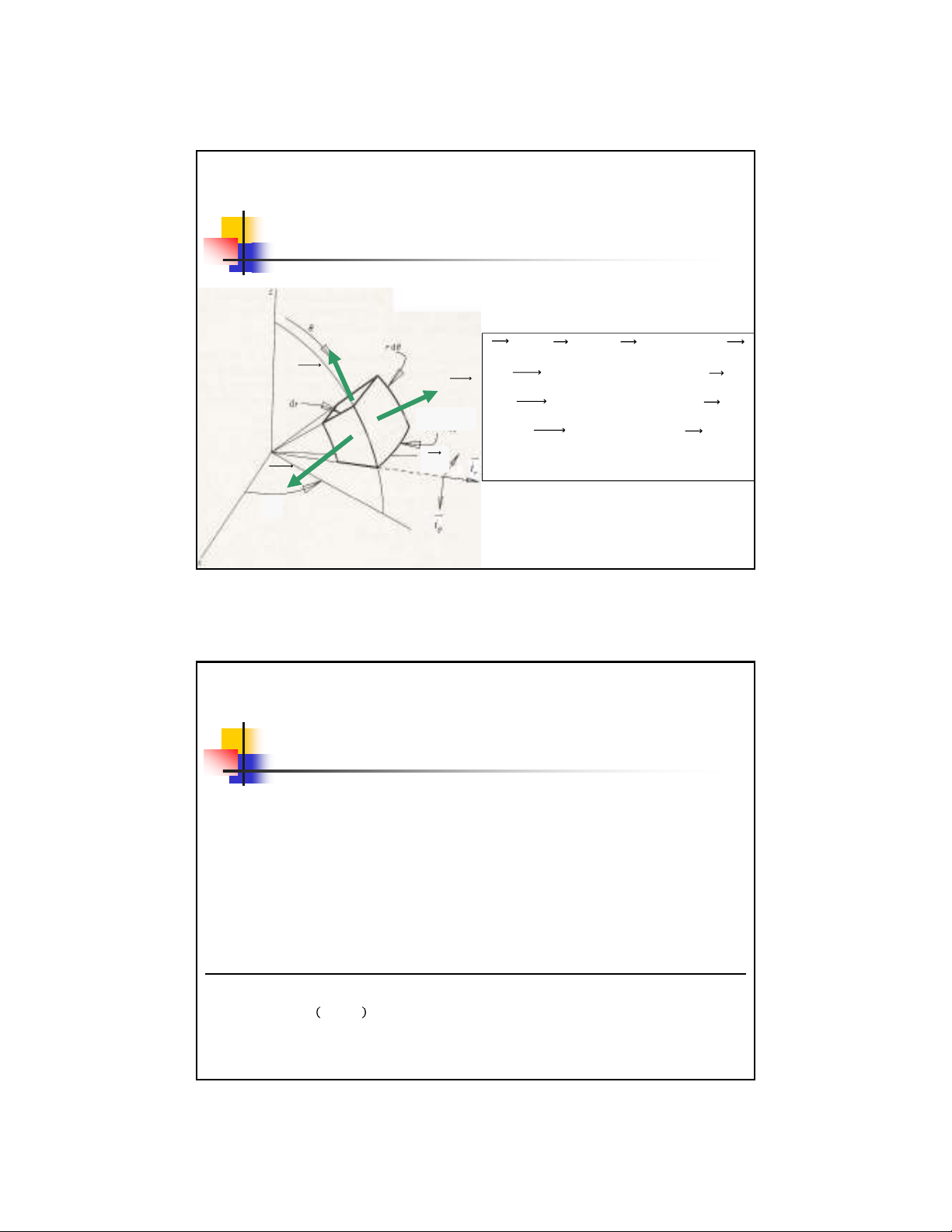
5
7:43 AM Chương 1 9
Các yếutốvi phân
Hệtoạđộcầu
rsind
7:43 AM Chương 1 10
Các yếutốvi phân
Tìm khốilượng củavậtthểhình cầu bán kính a, tâm tạigốctoạđộcó mậtđộ khốilượng
(r,,)=0/r.
m=20a2
Tìm tích phân
vớiVlànửatrênhìnhcầu bán kính R.
Áp dụng: r: 0 – R, :0-2,:0-/2
x=rsincos
y=rsinsin


























