
1
Tröôøng ñieän töø
ªChöông 1 : Khaùi nieäm & phtrình cô baûn cuûa TÑT
ªChöông 2 : Tröôøng ñieän tónh (TÑt)

2
Chöông 2 : Tröôøng ñieän tónh
1. Khaùi nieäm chung
2. Tính chaát theá cuûa tröôøng ñieän tónh
3. Phöông trình Poisson-Laplace & ÑKB
4. Vaät lieäu trong TÑt
5. Naêng löôïng tröôøng ñieän
6. Löïc ñieän
7. Phöông phaùp tính TÑt
3
1. Khaùi nieäm chung
ª Ñònh nghóa TÑT tónh :
0, 0J
t
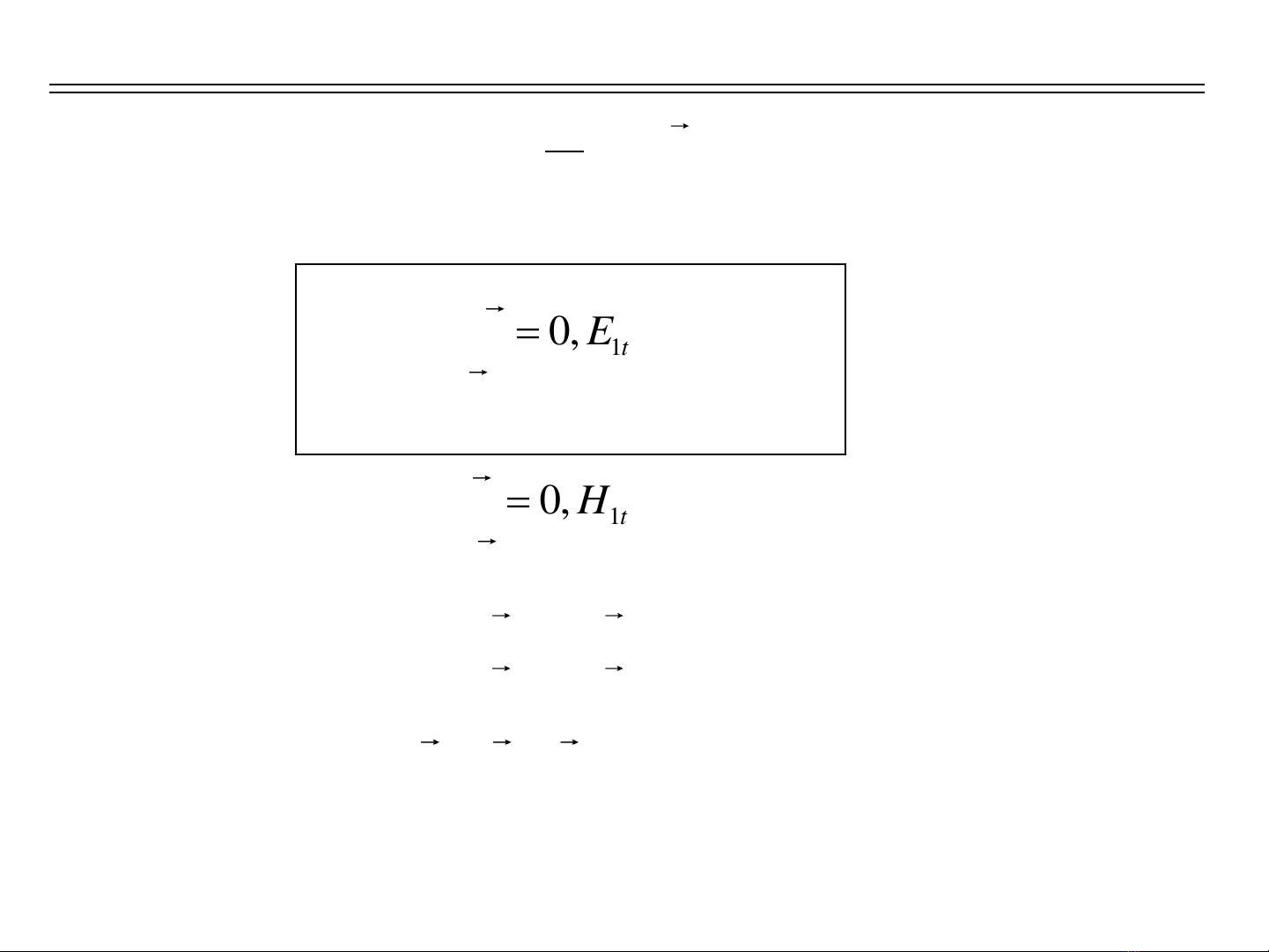
12
12
0, 0
() ,
tt
nn
rotE E E
AdivD D D
ª Moâ hình toaùn :
12
12
0, 0
() 0, 0
tt
nn
rotH H H
BdivB B B
TÑ tónh (A) :
TT tónh (B):
0, 0EH
0, 0EH
0P E H
Khoâng coù söï lan truyeàn naêng löôïng ñieän töø
trong TÑT tónh

4
Chöông 2 : Tröôøng ñieän tónh
1. Khaùi nieäm chung
2. Tính chaát theá cuûa tröôøng ñieän tónh
2.1. Coâng cuûa löïc ñieän tónh
2.2. Theá voâ höôùng
2.3. Ví duï

5
2.1. Coâng cuûa löïc ñieän tónh
... 0
CC
Fdl qEdl
Coâng tduïng leân ñtích ñieãm treân ñöôøng cong kín luoân baèng 0
Coâng chæ phuï thuoäc ñieåm ñaàu & ñieåm cuoái maø khoâng phuï
thuoäc ñöôøng ñi
Keát luaän : TÑ tónh laø moät tröôøng theá
... AaB AbB
Fdl Fdl











![Thí nghiệm Vật lí (BKEM-012): Tài liệu [Mô tả/Hướng dẫn/Bài tập,...]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251219/thanhlong020907@gmail.com/135x160/54561766129946.jpg)














