PH N BÀI T PẦ Ậ
I. CON L C LÒ XOẮ
1. Cho pt: x = 4cos 4t (cm)
Tính: a) f = ?
b) x, v = ? khi t = 5s.
H ng d n:ướ ẫ
Pt: x = 4cos 4t.
a. T n s : ầ ố
)Hz(2
2
4
2
f=
π
π
=
π
ω
=
b. * Khi t = 5s, thay vào pt x, ta có: x = 4 cos20 = 4 (cm)
* T pt x => v = x’ = -16. sin4t ừ
Thay t = 5s vào pt v, ta có: v = -16  sin20 = 0 (cm/s)
2. Cho: con l c lò xo có kh i l ng c a hòn bi là m, dao đ ng v i T = 1s.ắ ố ượ ủ ộ ớ
a. Mu n con l c dao đ ng v i chu kỳ ố ắ ộ ớ
T' = 0,5s thì hòn bi ph i có kh i l ng m' b ng bao nhiêu?ả ố ượ ằ
b. N u thay hòn bi b ng hòn bi có kh i l ng m' = 2m, thì chu kỳ c a con l c s là bao nhiêu?ế ằ ố ượ ủ ắ ẽ
c. Trình bày các dùng con l c lò xo đ đo kh i l ng c a m t v t nh ?ắ ể ố ượ ủ ộ ậ ỏ
H ng d n:ướ ẫ
a. Chu kỳ dao đ ng c a con l c lò xo: ộ ủ ắ
k
m
2T
π=
G i m' là c a con l c có ọ ủ ắ chu kỳ T' = 0,5s, ta có:
k
'm
2'T
π=
L p t s : ậ ỉ ố
m
'm
k
m
2
k
'm
2
T
'T =
π
π
=
=>
4
m
'm
4
1
1
5,0
T
'T
2
2
2
2
== >===
m
m'
b. T bi u th c: ừ ể ứ
22
2
2
T
m
'm
'T
T
'T
== >=
m
m'
Thay: m' = 2m => T'2 =2m/m.1 = 2 =>
)s(4,12'T ==
c. – M c m t v t đã bi t kh i l ng m vào m t lò xo đ t o thành m t con l c lò xo. Cho nó daoắ ộ ậ ế ố ượ ộ ể ạ ộ ắ
đ ng trong th i gian t(s) ta đ m đ c n dao đ ng, theo đ nh nghĩa ộ ờ ế ượ ộ ị chu kỳ ta xác đ nh đ c: ị ượ
- Mu n đo v t có kh i l ng m' (ch a bi t), ta thay m b ng m' , sau đó cho dao đ ng và tính đ cố ậ ố ượ ư ế ằ ộ ượ
T' nh trên.ư
- Bi t m, T, T' ta tính đ c: ế ượ
m
T
'T
'm
2
2
=
3. Cho m t con l c dao đ ng v i biên đ A = 10cm, chu kỳ T = 0,5s. Vi t pt dao đ ng c a con l cộ ắ ộ ớ ộ ế ộ ủ ắ
trong các tr ng h p:ườ ợ
a. Ch n t = 0: v t v trí cân b ng.ọ ậ ở ị ằ
b. Ch n t = 0: v t cách v trí cân b ng m t đo n 10cm.ọ ậ ở ị ằ ộ ạ
H ng d n:ướ ẫ
D ng t ng quát c a pt: x = A sin(wt+).ạ ổ ủ
V i: ớ
)s/rad(4
5,0
2
T
2π=
π
=
π
=ω
V y: x = 10 sin (4t + ) (cm)ậ(1)
Tính 
a. Cho t = 0 khi v t v trí cân b ng, nghĩa là x = 0. ậ ở ị ằ
Thay (1) ta có: 0 = 10 sin  => sin
V y, pt có d ng: x = 10 sin 4t (cm)ậ ạ
b. Cho t = 0 khi x = 10cm.
Thay vào (1), ta có: 10 = 10 sin  sin
V y: pt s thành: x = 10 sin (4t + /2) (cm)ậ ẽ
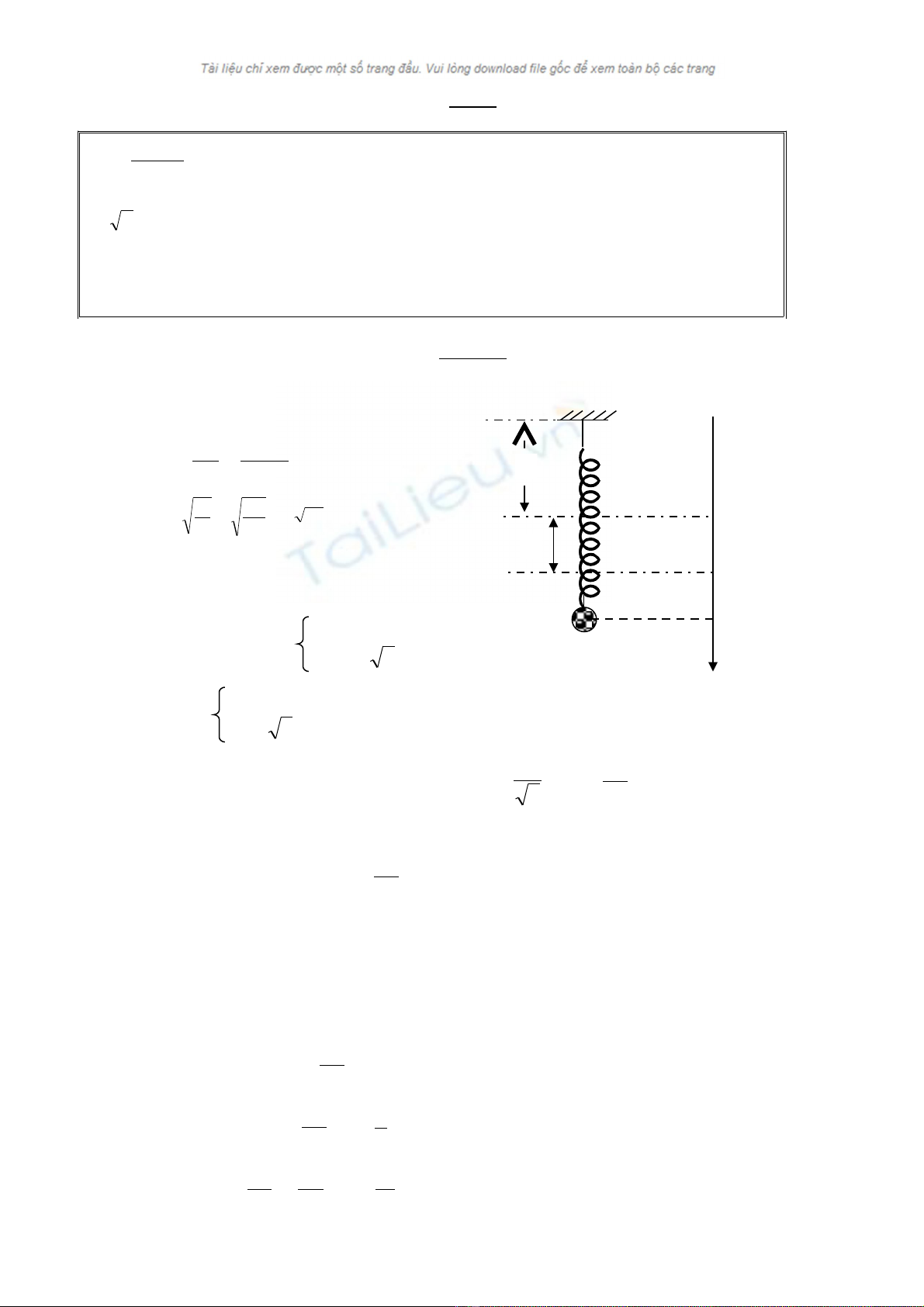
Bài 4: M t lò xo đ c treo th ng đ ng, đ u trên c a lò xo đ c gi c đ nh, đ uộ ượ ẳ ứ ầ ủ ượ ữ ố ị ầ
d i theo v t n ng có kh i l ng m = 100g, lò xo có đ c ng k = 25 N/m. Kéo v t r iướ ậ ặ ố ượ ộ ứ ậ ờ
kh i VTCB theo ph ng th ng đ ng h ng xu ng m t đo n 2cm, truy n cho nó v n t cỏ ươ ẳ ứ ướ ố ộ ạ ề ậ ố
310
.
π
(cm/s) theo ph ng th ng đ ng h ng lên. Ch n g c thươ ẳ ứ ướ ọ ố i gianờ là lúc th v t,ả ậ
g c to đ là VTCB, chi u d ng h ng xu ng.ố ạ ộ ề ươ ướ ố
a. Vi t PTDĐ.ế
b. Xác đ nh th i đi m v t đi qua v trí mà lò xo giãn 2 cm l n th nh t.ị ờ ể ậ ị ầ ứ ấ
L i gi iờ ả
a) T i VTCBOạ
k∆l = mg
⇒ ∆l =
0,04
25
0,1.10
k
mg ==
(m)
+ ω =
π===
5105
1,0
25
m
k
(Rad/s)
+ m dao đ ng đi u hòa v i ph ng trìnhộ ề ớ ươ
x = Asin (ωt + ϕ)
T i th i đi m t = 0 x = 2 cm > 0ạ ờ ể
v = 10π
3
(cm/s) <0
Ta có h 2 = ASin ệϕ →Sin ϕ >0
-10π
3
= 5π.Acosϕ →cosϕ <0
Chia 2 v c a hai ph ng tr nh tr n ta cú: tgế ủ ươ ỡ ờ ϕ =
3
1−
⇒ ϕ =
6
5
π
(Rad) → A = 4(cm)
V y PTDĐ:ậ
x = 4sin (5πt +
6
5
π
) (cm)
b) T i VTCB lò xo dãn ạ∆l = 4cm
+ th i đi m t = 0, lò xo b dãn ở ờ ể ị ∆l = 4 + 2 = 6 (cm)
+ th i đi m t = 0 , v t đi lên v<0, t i v trí lò xo b dãn 2cm l n đ u tiên thì v<0.ở ờ ể ậ ớ ị ị ầ ầ
V y lúc đó x = -2 (cm)ậ
Ta có: -2 = 4sin (5πt +
6
5
π
)
⇔ sin (5πt +
6
5
π
) =
2
1
−
5πt +
6
5
π
=
6
7
π
⇒ t =
15
1
(s)
∆l
l0
0(VTCB)
)
x
- ∆l
•
•
•
( Có th gi i b ng m i liên h gi a dao đ ng đi u hoà và chuy n đ ng tròn đ u)ể ả ằ ố ệ ữ ộ ề ể ộ ề
Bài 5: Cho con l c lò xo dđđh theo ph ng th ng đ ng v t n ng có kh i l ng mắ ươ ẳ ứ ậ ặ ố ượ
= 400g, lò xo có đ c ng K, co năng toàn ph n E = 25mJ. T i th i đi m t = 0, kéo mộ ứ ầ ạ ờ ể
xu ng d i VTCB đ lò xo giãn 2,6cm đ ng th i truy n cho m v n t c 25cm/s h ng lênố ướ ể ồ ờ ề ậ ố ướ
ng c chi u d ng Ox (g = 10m/sượ ề ươ 2)
a. CM v t dđđh.ậ
b. Vi t PTDĐế
L i gi iờ ả
a. T i VTCBạ k∆l = mg ⇒ k∆l = 0,4.10 = 4 → ∆l =
k
4
(mét)
T i th i đi m t = 0, kéo m xu ng d i VTCB, lò xo dãn 2,6 cmạ ờ ể ố ướ
→ x = 2,6 - ∆l = 0,026 -
k
4
( mét)
Chi u d ng 0x h ng xu ng ề ươ ướ ố ⇒ x >0
T i t = 0 ạ x = 0,026 m/s > 0
v = -0,25 m/s <0
C năng toàn ph n E = ơ ầ
3
10.25
2
2
1
2
2
1−
=+ mvkx
(J)
Ta có ph ng trình:ươ
322 25.10).0,4.(0,25
2
1
)
k
4
k(0,026
2
1−
=+−
⇔k(2,6.10-2 -
025,0)
42=
k
⇔0,0262.k2 - 0,233k + 16 = 0 ⇔ k = 250 (N/m) TM
k = 94,67 (N/m) lo iạ
V y k = 250 N/m ậ→ ω =
25
4,0
250 ==
m
k
(Rad/s)
T i t = 0 x = 1cm ạ> 0
v = -25cm/s < 0
1 = Asin ; sinϕ >0 ϕ =
4
3π
Rađ
-25 = 25Acosϕ; cosϕ<0 A =
2
cm
V y ph ng trình đi u hoà là x = ậ ươ ề
)
4
3
t25sin(2 π
+
(cm)
=> k > 153,8 N/m
Bài 6: Treo m t v t có kh i l ng m1 thì chu kì dao đ ng Tộ ậ ố ượ ộ 1 = 3s. Thay v t m1 b ng v t kh iậ ằ ậ ố
l ng m2 vào lò xo thì chu kì dao đ ng Tượ ộ 2 = 4s. N u treo đ ng th i m1 và m2 vào lò xo đó thì chu kìế ồ ờ
dao đ ng đó là bao nhiêu?ộ
Bài 7: M t v t n ng có kh i l ng m = 100g, g n vào m t lò xo có kh i l ng không đáng k , đ uộ ậ ặ ố ượ ắ ộ ố ượ ể ầ
kia treo vào m t đi m c đ nh, v t dao đ ng đi u hòa theo ph ng th ng đ ng v i t n s f = 10/Пộ ể ố ị ậ ộ ề ươ ẳ ứ ớ ầ ố
Hz. Trong quá trình dao đ ng đ dài c a lò xo lúc ng n nh t là 40cm, lúc dài nh t 44cm. Ch n g cộ ộ ủ ắ ấ ấ ọ ố
th i gian lúc v t qua v trí cân b ng theo chi u d ng. Vi t ph ng trình dao đ ng c a v t.ờ ậ ị ằ ề ươ ế ươ ộ ủ ậ
Bài 8: M t con l c lò xo g m m t kh i c u nh g n vào đ u m t lò xo, dao đ ng đi u hòa v iộ ắ ồ ộ ố ầ ỏ ắ ầ ộ ộ ề ớ
biên đ 3cm d c theo tr c Ox, v i chu kì 0,5s, vào th i đi m t = 0, kh i c u qua v trí cân b ng theoộ ọ ụ ớ ờ ể ố ầ ị ằ
chi u d ng. Kh i c u có li đ x = 1,5cm l n đ u tiên vào th i đi m nào.ề ươ ố ầ ộ ầ ầ ờ ể
Bài 9: Treo vào lò xo m t v t có kh i l ng m th y nó b kéo dãn, dài thêm 90mm. Dùng tay kéoộ ậ ố ượ ấ ị
v t xu ng th p theo ph ng th ng đ ng m t đo n dài 36mm r i buôn tay ra. Th i gian th c hi nậ ố ấ ươ ẳ ứ ộ ạ ồ ờ ự ệ
40 dao đ ng toàn ph n đo đ c là t = 24s. L y П = 3,14. Tính gia t c tr ng tr ng t i n i làm thíộ ầ ượ ấ ố ọ ườ ạ ơ
nghi m?ệ
Bài 10: M t ch t đi m dao đ ng đi u hòa v i ph ng trình x = 6sin(Пt + П/2)cm. ộ ấ ể ộ ề ớ ươ
a. Tính v n t c c a ch t đi m t i th i đi m t = 0,5s.ậ ố ủ ấ ể ạ ờ ể
b. Tính v n t c c a ch t đi m ng v i li đ 6cm.ậ ố ủ ấ ể ứ ớ ộ
Bài 11: M t v t có kh i l ng 2kg treo vào m t lò xo có h s đàn h i k = 5000N/m. Khi kéo v tộ ậ ố ượ ộ ệ ố ồ ậ
ra kh i v trí cân b ng m t đo n 5cm r i th không v n t c đ u. ỏ ị ằ ộ ạ ồ ả ậ ố ầ
a. Tính chu kì dao đ ng.ộ
b. Tính v n t c c c đ i c a v t.ậ ố ự ạ ủ ậ
Bài 12: M t v t có kh i l ng m treo b ng m t lò xo vào m t đi m c đ nh O thì dao đ ng v i t nộ ậ ố ượ ằ ộ ộ ể ố ị ộ ớ ầ
s 5Hz. Treo thêm m t v t kh i l ng Δm = 38g vào v t thì t n s dao đ ng là 4,5Hz. Tính đố ộ ậ ố ượ ậ ầ ố ộ ộ
c ng k c a lò xo. L y П = 10.ứ ủ ấ
Bài 13: Qu c u kh i l ng m = 100g treo vào lò xo đ c ng k = 10N/m. T v trí cân b ng Oả ầ ố ượ ộ ứ ừ ị ằ
( ch n làm g c t a đ ) ta kéo th ng qu c u xu ng đo n OM = 2cm r i truy n v n t c có đ l nọ ố ọ ộ ẳ ả ầ ố ạ ồ ề ậ ố ộ ớ
20cm/s theo ph ng th ng đ ng h ng lên. Ch n t = 0 là lúc qu c u qua v trí cân b ng O l n đ uươ ẳ ứ ướ ọ ả ầ ị ằ ầ ầ
tiên, chi u d ng h ng xu ng. Vi t ph ng trinh dao đ ng c a qu c u.ề ươ ướ ố ế ươ ộ ủ ả ầ
Bài 14: Con l c lò xo dao đ ng v i biên đ A = 10cm, li đ x = 2,5cm. Thì quan h gi a đ ngắ ộ ớ ộ ở ộ ệ ữ ộ
năng và th năng nh th nào?ế ư ế
II. CON L C Đ NẮ Ơ
Bài 15:
Hai con l c đ n chi u dài lắ ơ ề 1, l2 (l1>l2) và có chu kì dao đ ng t ng ng là Tộ ươ ứ 1; T2,
t i n i có gia t c tr ng tr ng g = 9,8m/sạ ơ ố ọ ườ 2. Bi t r ng, cũng t i n i đó, con l c có chi uế ằ ạ ơ ắ ề
dài l1 + l2 , chu kì dao đ ng 1,8s và con l c đ n có chi u dài lộ ắ ơ ề 1 - l2 có chu kì dao đ ng 0,9ộ
(s). Tính T1, T2, l1, l2.
L i gi iờ ả
+ Con l c chi u dài lắ ề 1 có chu kì T1=
g
l
.2 1
π
→ l1=
g.
4
T
2
2
1
π
(1)
+ Co l c chi u dài lắ ề 2có chu kì T2=
g
l
.2 2
π
→ l1=
g.
4
T
2
2
2
π
(2)
+ Con l c chi u dài lắ ề 1 + l2 có chu kì T3= 2Π.
g
ll 21 +
→ l1 + l2 =
81,0
4
10.)8,0(
4
g.)T(
2
2
2
2' =
π
=
π
(m) = 81 cm (3)
+ Con l c có chi u dài lắ ề 1 - l2có chu kì T' = 2Π.
g
ll 21 −
→ l1 - l2 =
2025,0
4
10.)9,0(
4
g.)T(
2
2
2
2' =
π
=
π
(m) = 20,25 cm (4)
T (3) (4) ừl1= 0,51 (m) = 51cm
l2 = 0,3 (m) = 3cm
Thay vào (1), (2) T1= 2Π
42,1
10
51,0 =
(s) Suy ra T2= 2Π
1,1
10
3,0 =
(s)
Bài 16:
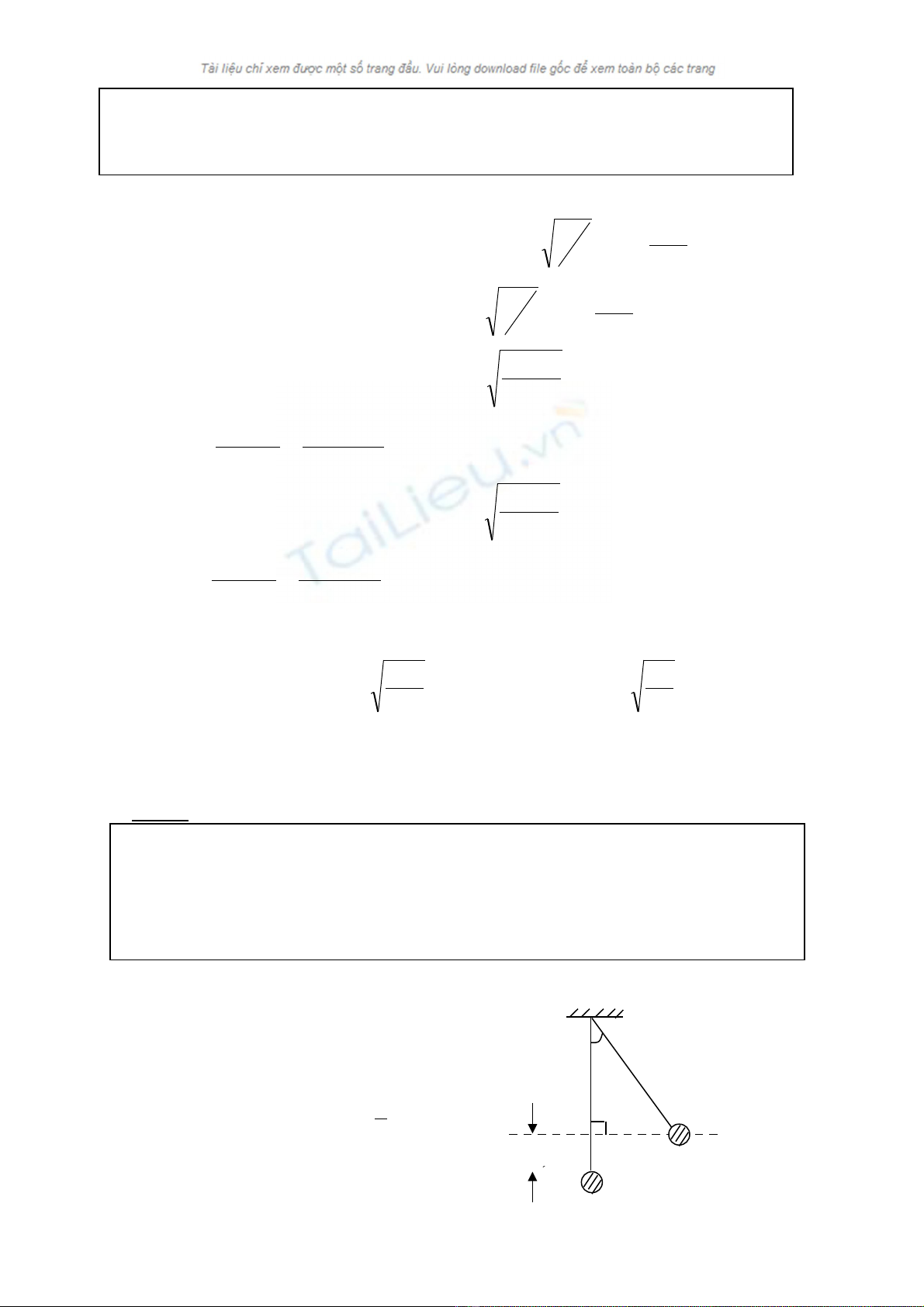
M t con l c có chi u dài l, v t n ng kh i l ng m, kéo con l c ra kh i VTCBộ ắ ề ậ ặ ố ượ ắ ỏ
m t góc ộα0 r i th không v n t c đ u.ồ ả ậ ố ầ
1. L p BT v n t c t ng ng v i li đ góc ậ ậ ố ươ ứ ớ ộ α suy ra BT v n t c c c đ i.ậ ố ự ạ
2. L p bt l c căng dây ng v i li đ góc ậ ự ứ ớ ộ α. Suy tab t l c căng dây c c đ i, c cự ự ạ ự
ti u.ể
* áp d ng: l = 1m, m = 100g, ụα0 = 60 ; g = 10(m/s2);
π
2= 10
L i gi iờ ả
1. BT v n t c t ng ng v i li đ ậ ố ươ ứ ớ ộ α
+ Theo đ nh lu t b o toàn c năng, c năng c aị ậ ả ơ ơ ủ
con l c t i VT li giác b t kì b ng th năng c a con l cắ ạ ấ ằ ế ủ ắ
t i VT biên.ạ
mgh0 = mgh +
2
1
(mv2)
→ v2 = 2g (h0 - h)2 (v2 = 2gl (1 - cos)
V i hớ0 = l(1 - cosα) h = l(1 - cosα)
I
α
h0 - h