Chương 1: Mô hình toán kinh tế

Chia sẻ: Lan Lan | Ngày: | Loại File: PDF | Số trang:68

Thêm vào BST

Báo xấu

383
lượt xem 83
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Mô hình của một đối tượng là sự phản ánh khách quan về đối tượng đó, bằng ngôn ngữ nói, viết, hình vẽ, hoặc ngôn ngữ chuyên ngành. Mô hình của các đối tượng trong lĩnh vực kinh tế, gọi là mô hình kinh tế. Mô hình toán kinh tế, là mô hình kinh tế, được trình bày bằng ngôn ngữ toán học. 2 .TD1: Nghiên cứu quá trình hình thành giá của loại hàng hóa A trên thị trường. Mô hình bằng lời: Xét thị trường hàng hóa A, nơi có người bán, người mua gặp nhau. Với mức giá p,...

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Chương 1: Mô hình toán kinh tế

Chương 1: Mô hình toán kinh tế 1. Khái niệm về mô hình toán kinh tế 2. Cấu trúc mô hình toán kinh tế 3. Phân tích mô hình toán kinh tế 4. Áp dụng đối với một số mô hình kinh tế phổ biến (Tài liệu tham khảo: Mô hình toán kinh tế; ĐHKTQD Hà nội-Nguyễn Quang Dong) B2 1
1. Khái niệm về mô hình toán kinh tế Mô hình của một đối tượng là sự phản ánh khách quan về đối tượng đó, bằng ngôn ngữ nói, viết, hình vẽ, hoặc ngôn ngữ chuyên ngành. Mô hình của các đối tượng trong lĩnh vực kinh tế, gọi là mô hình kinh tế. Mô hình toán kinh tế, là mô hình kinh tế, được trình bày bằng ngôn ngữ toán học. 2
TD1: Nghiên cứu quá trình hình thành giá của loại hàng hóa A trên thị trường. Mô hình bằng lời: Xét thị trường hàng hóa A, nơi có người bán, người mua gặp nhau. Với mức giá p, lượng hàng người bán muốn bán gọi là lượng hàng cung S, lượng hàng người mua muốn mua gọi là lượng hàng cầu D. Khi cung lớn hơn cầu thì giá sẽ có xu hướng giảm, Khi cầu lớn hơn cung thì giá sẽ có xu hướng tăng. Quá trình tiếp diễn như vậy, cho đến khi cung băng cầu, sẽ hình thành mức giá p , gọi là mức giá cân bằng. 3
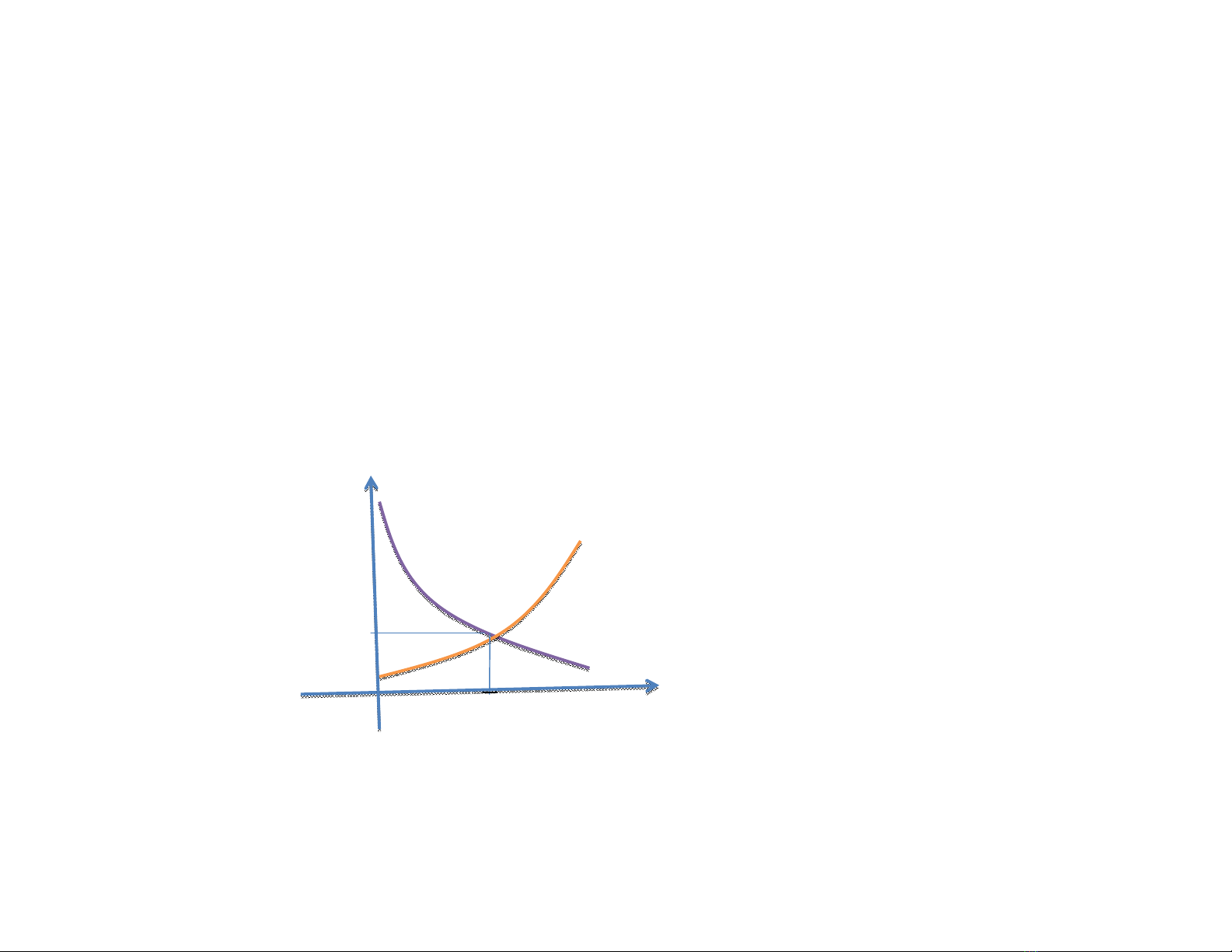
Mô hình bằng hình bằng hình vẽ Trong hệ trục tọa độ vuông góc p0q, ta vẽ đường cầu D, đường cung S, điểm hai đường cong gặp nhau là điểm cân bằng Q D S q0 op p 4
Mô hình toán kinh tế: Với mỗi mức giá p, khối lương hàng cung là S=S(p); khối lượng hàng cầu D=D(p). Do người bán sẵn sàng bán giá cao hơn nên S’(p)>0, do người mua muốn mua giá thấp hơn nên D’(p)0 D=D(p) D’(p)
Khi muốn đề cập đến thu nhập M, và mức thuế T vào quá trình hình thành giá ta có mô hình toán kinh tế (MHIB): S=S(p,M,T) S’p= dS/dp >0 D=(p,M,T) D’p= dD/dp
2. Cấu trúc mô hình toán kinh tế 2.1. Các biến số, tham số trong mô hình 2.2. Mối liên hệ giữa các biến số trong mô hình 7
2.1. Các biến số của mô hình Mỗi yếu tố kinh tế được lượng hóa bằng một đại lượng x,y,z.. gọi là một biến số. Biến nội sinh (biến được giải thích). Là các biến thể hiện các hiện tượng kinh tế, mà giá trị của chúng phụ thuộc vào các biến khác trong mô hình. Biến ngoại sinh (biến giải thích). Là các biến độc lập với các biến khác, và giá trị của chúng được xem là tồn tại ngoài mô hình. 8
Thí dụ: Một doanh nghiệp muốn sản xuất một khối lượng hàng hóa loại A là Q, thì cần có n yếu tố đầu vào x1,x2,..,xn. Các yếu tố kinh tế này liên hệ với nhau bởi quan hệ hàm Q = f(x1,x2,..,xn,α,β). Khi đó ta có mô hình hàm sản xuất của doanh nghiệp: Q = f(x1,x2,..,xn,α,β) xi  o i Trong mô hình này Q là biến nội sinh, xi là biến ngoại sinh α, β là các tham số Trong mô hình MHIB của loại hàng hóa A, nếu S = αpβTγ Khi đó các biến S,D,p là các biến nội sinh; T,M là biến ngoại sinh; α, β, γ là các tham số. 9
2.2. Mối liên hệ giữa các biến Để mô tả các mối quan hệ kinh tế, các quy luật kinh tế trong các mô hình toán kinh tế người ta thường dùng các phương trình hoặc bất phương trình. Phương trình định nghĩa thể hiện quan hệ định nghĩa giữa các biến. Phương trình hành vi mô tả quan hệ giữa các biến do tác động của các quy luật kinh tế, hoặc do giả thiết. Phương trình điều kiện mô tả quan hệ giữa các biến trong tình huống có điều kiện. 10
Thí dụ: PT định nghĩa:  = TR-TC (lợi nhuận=doanh thu- chi phí); NX=EX-IM (Xuất khẩu ròng=xuất khẩu- nhập khẩu) PT hành vi: Trong mô hình MHIA: S = S(p); D=D(p); S=D Phương trình điều kiên: Trong mô hình hàm sản xuất bất phương trình xi0 là bất phương trình điều kiện. 11
3. Phân tích mô hình toán kinh tế 3.1. Đo lường sự thay đổi của biến nội sinh theo biến ngoại sinh 3.2. Hệ số tăng trưởng (nhịp tăng trưởng) 3.3. Hệ số thay đổi (bổ sung, chuyển đổi) 12
3.1. Đo lường sự thay đổi của biến nội sinh theo biến ngoại sinh a) Sự thay đổi tuyệt đối Xét quan hệ kinh tế y = f(x1,x2,..xn) tại x=(x1,x2,..,xn). Cho xi thay đổi một lượng nhỏ xi, khi đó y thay đổi một lượng tương ứng là: y = f(x1,x2,..,xi+xi,..,xn) - f(x1,x2,..,xn). Lượng thay đổi trung bình của y theo xi là: y  xi  x i Nếu f khả vi theo biến xi ta gọi xu hướng thay đổi của biến nội sinh y theo biến ngoại sinh xi tại x, là biên tế của y theo xi, kí hiệu My(xi) f My( x i )   ( x i ) x i 13
Nếu tất cả các biến ngoại sinh xi đều thay đổi một lượng nhỏ xi thì độ thay đổi của y là: n f y  dy   dx i i 1 x i Nếu xi là biến nội sinh phụ thộc vào một biến khác, thì ta sử dụng công thức tính vi phân của hàm hợp. TD: Chi phí C(Q) phụ thuộc vào sản lượng Q và có mô hình chi phí sản xuât của doanh nghiệp là: C(Q) = Q3-61.25Q2+1528.5Q+2000 Chi phí biên tế của theo Q (chi phí cận biên), kí hiệu MC(Q) = 3Q2-122,5Q+1528.5 14
b) Sự thay đổi tương đối Ta gọi hệ số co giãn của biến y theo biến xi tại điểm x là: y y x i x   i x i y Hệ số này cho biết tại x khi xi thay đổi 1% thì y y  thay đổixi %. y Nếu  xi >0 thì xi và y biến thiên cùng chiều y Nếu  xi
Nếu gọi Mfi = là hàm cận biên của y theo xi; Afi=y/xi là hàm trung bình của y theo xi. khi đó ta có: yxi = Mfi/Afi Nếu y=u(x)v(x)  yx=ux+ vx y=u/v  yx=ux-vx TD: Khi mô hình sản xuất có dạng Q = aKαLβ, với α>0 β>0, Q là mức sản lượng, K là vốn, L là khối lượng lao động. q  L = β; = α; q = α+β 16
3.2. Hệ số tăng trưởng (nhịp tăng trưởng) Khi trong mô hình có biến ngoại sinh là biến thời gian t, giả sử y = f(x1,x2,..,xn,t), khi đó ta dùng hệ số tăng trưởng để đo sự thay đổi của biến nội sinh theo thời gian t. y / t Hệ số tăng trưởng của y là ry  , thường ry y được theo theo tỷ lệ % TD: Theo công thức tính lã gộp liên tục tại thời điểm ta có: vt=v0ert có hệ số tăng trưởng rv=r Nếu lãi suất tính theo từng kỳ thì vt=v0(1+r)t có hệ số tăng trưởng rv=ln(1+r)r 17
Cho: u = g(t); v = h(t) Nếu y = uv  ry = ru + rv Nếu y = u/v  ry = ru – rv u v Nếu y = u + v  ry = ru  rv uv uv u v Nếu y = u - v  ry = ru  rv uv uv n Cho: y = f[x1(t),x2(t),..,xn(t)]  ry =   xyi rxi i 1 18
3.3. Hệ số bổ sung, chuyển đổi Cho y = f(x1,x2,..,xn), nếu cho 2 biến ngoại sinh xi, xj thay đổi và cố định các biến khác sao cho y không đổi. Từ biểu thức vi phân của hàm y n y y y dy   dx i 0  dx i  dx j i 1 x i x i x j dx i f / x j   dx j f / x i Hệ số này cho biết khi gia giảm xj một đơn vị, thì phải gia giảm xi bao nhiêu đơn vị để y không thay đổi. 19
Nếu dxi/dxj0 thì ta nói xi xj có thể bổ sung được cho nhau với tỷ lệ dxi/dxj, và gọi là hệ số bổ sung cận biên của xi cho xj Nếu dxi/dxj=0 thì ta nói xi, xj không thay thế được cho nhau hoặc không bổ sung được cho nhau. 20