CH NG IIƯƠ : H TH C L NG TRONG TAM GIÁC VÀ TRONG Đ NGỆ Ứ ƯỢ ƯỜ
TRÒN.
BÀI 1: T S L NG GIÁC C A GÓC B T KỲ.Ỉ Ố ƯỢ Ủ Ấ
N I DUNGỘ
I/M Đ U:Ở Ầ
C Sin
α
=
AC
BC
Cos
α
=
AB
BC
A B
tg
α
=
AC
AB
cotg
α
=
AB
AC
II/T S L NG GIÁC C A GÓC Ỷ Ố ƯỢ Ủ
0 0
(0 180 )
α α
≤ ≤
:
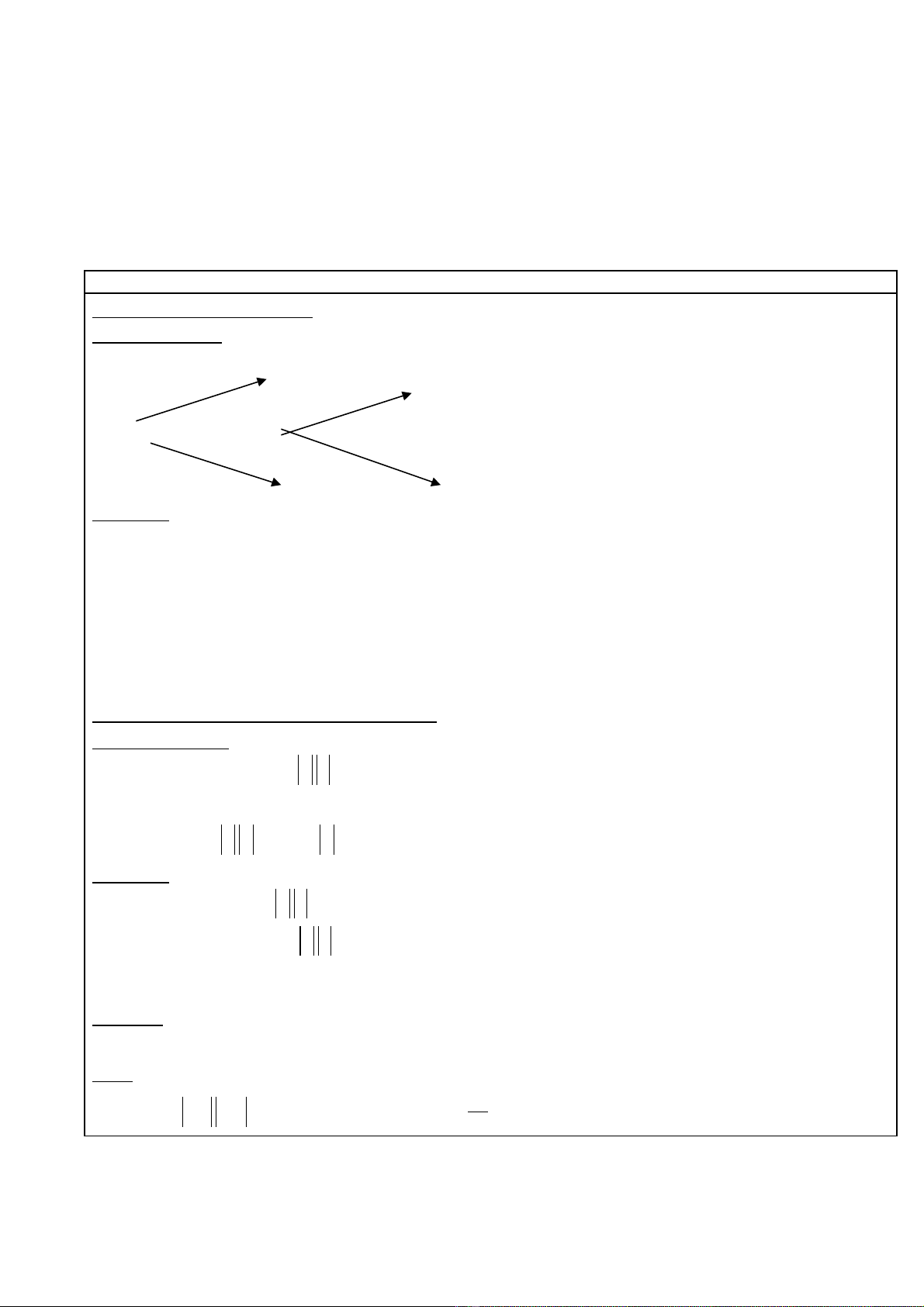
Trên h to đ Oxy cho A(1;0),B(0;1),A’(-1;0).ệ ạ ộ
Xét n a đ ng tròn đk AA’ đi qua B đ c g i là n a đ ng tròn đ n v .ử ườ ượ ọ ử ườ ơ ị
L y M trên n a đ ng tròn đ n v sao cho góc AOM=ấ ử ườ ơ ị
α
M có to đ M(x;y).ạ ộ
Đ NH NGHĨAỊ:
*Tung đ y c a đi m M g i là sin c a góc ộ ủ ể ọ ủ
α
,KH:sin
α
Vi t sinế
α
=y.
*Hoành đ x c a đi m M g i là cosin c a ộ ủ ể ọ ủ
α
,KH:cos
α
, vi t cosế
α
=x.
*T s ỷ ố
( 0)
yx
x≠
g i là tang c a góc ọ ủ
α
,KH:tg
α
, vi t tgế
α
=
y
x
*T s ỷ ố
( 0)
xy
y≠
g i là cotang c a góc ọ ủ
α
,KH:cotg
α
, vi t cotgế
α
=
x
y
Ví d :ụ
a)Tính sin
α
,
α
=300
Đ t ặ
=300,G i Mọ1,M2 l n l t là hchi u c a M xu ng Ox,Oy.ầ ượ ế ủ ố
Xét tam giác MM1O,ta có đó là n a tam giác đ u có c nh bên b ng 1,nên MMử ề ạ ằ 1=1/2.
V y sin 30ậ0 =
2 1
1
2
OM M M= =
T ng t Hs tính Cos 30ươ ự 0,tg300,cotg300.
II/T S L NG GIÁC C A M T S GÓC C N NH :Ỷ Ố ƯỢ Ủ Ộ Ố Ầ Ớ
góc 003004506009001200135015001800
Trang 1
Sin 0
1
2
2
2
3
2
1
3
2
2
2
1
2
0
Cos 1
3
2
2
2
1
2
0-
1
2
2
2
−
3
2
−
-1
Tg 0
3
3
1
3
|| -
3
-1
-
3
3
0
cotg ||
3
1
3
3
0
3
3
−
-1 -
3
||
IV/D U C A CÁC T S L NG GIÁC:Ấ Ủ Ỷ Ố ƯỢ
•sin
α
0,
α
≥ ∀
.
•
0 0
0 90 0 cos 1
α α
< < ⇒ < <
•
0 0
90 180 1 cos 0
α α
< < ⇒ − < <
•Các t s tgỷ ố
α
và cotg
α
,n u khác không thì chúng cùng d u v i cosế ấ ớ
α
.
CÁC H TH C GI A CÁC T S L NG GIÁCỆ Ứ Ữ Ỉ Ố ƯỢ
N I DUNGỘ
I.CÁC H TH C C B N:Ệ Ứ Ơ Ả
1.Đ NH LÝ:ỊV i m i góc ớ ọ
α
ta đ u có:ề
a)N u Cosế
α
≠
0 thì
sin (1)
cos
tg
α
αα
=
b)N u Sin ế
α
≠
0 thì
cos
c (2)
sin
otg
α
αα
=
c)sin2
α
+cos2
α
=1 (3)
CM:SGK
2.VD:
Cho tgx+cotgx=2.Tính sinx.cosx=?
Gi iả:Tacó:
2 2
sin cos sin cos
cot cos sin sin .cos
1
sin .cos
x x x x
tgx gx x x x x
x x
+
+ = + =
=
Mà tgx+cotgx=2 nên ta đ c sinx.cosx=1/2.ượ
II.CÁC H TH C KHÁC:Ệ Ứ
1.Đ NH LÝ:Ị
N u cosế
α
≠
0 thì
2
2
1
1cos
tg
αα
+ =
(4)
Trang 2
N u sinế
α
≠
0 thì
2
2
1
1 cot sin
g
αα
+ =
(5)
tg
α
.cotg
α
=1 (6).
CM:SGK
2.VD:Đ n gi n bi u th c: ơ ả ể ứ
2
2
2 2
2 2
2 2
1 1 2cot
1 cos 1 cos
1 cos 1 cos 2cot
(1 cos )(1 cos )
2 2
2cot 2cot
1 cos sin
2 2cot 2cot 2
A g
g
g g
g g
α
α α
α α α
α α
α α
α α
α α
= + −
+ −
− + +
= −
+ −
= − = −
−
= + − =
V y A=2.ậ
III.LIÊN H GI A T S L NG GIÁC C A HAI GÓC BÙ NHAU:Ệ Ữ Ỉ Ố ƯỢ Ủ
Hai góc
α
và (1800-
α
) là hai góc bù nhau.Ta có:
Sin(1800-
α
)=sin
α
Cos (1800-
α
)=-cos
α
tg(1800-
α
) =-tg
α
cotg(1800-
α
) =-cotg
α
IV.LIÊN H GI A T S L NG GIÁC C A HAI GÓC PH NHAU:Ệ Ữ Ỉ Ố ƯỢ Ủ Ụ
Hai góc
α
và (900-
α
) là hai góc ph nhau.Ta có:ụ
Sin (900-
α
)=cos
α
Cos (900-
α
)=sin
α
tg(900-
α
)=cotg
α
cotg(900-
α
)=tg
α
VD:
1.Tính :
A=
0 0 0 0 0
cos20 cos 40 cos60 ... cos160 cos180+ + + + +
=Cos(1800-1600)+cos(1800-1400)+…+Cos 1600+cos1800
=-cos1600-cos1400+…+cos1600+cos1800=-1
V y A=-1.ậ
2.Cho tam giác ABC.CMR:
sin cos
2 2
A B C+=
Ta có A+B+C=1800 nên
0
90
2
A B C+ + =
0
90
2 2
A B C+
⇒ = −
0
sin sin 90
2 2
A B C+
⇒ = −
=
cos 2
C
(đpcm)
Trang 3
BÀI: TÍCH VÔ H NG C A HAI VECTƯỚ Ủ Ơ
N I DUNGỘ
I/GÓC C A HAI VECT :Ủ Ơ
1.Đ NH NGHĨA:ỊCho hai vect ơ
,a b
r r
khác
0
r
.T 1 đi m O ta v ừ ể ẽ
,OA a OB b= =
uuur r uuur r
.Khi đó s đo c a gócố ủ
AOB đ c g i là s đo c a góc gi a hai vect ượ ọ ố ủ ữ ơ
,a b
r r
,hay g n h n :Góc gi a hai vect ọ ơ ữ ơ
,a b
r r
.
Kh:
( )
,a b
r r
2.CHÚ Ý:
( )
,a b
r r
=00
⇔
a
r
cùng h ng ướ
b
r
.
( )
,a b
r r
=180
0
⇔
a
r
ng c h ng ượ ướ
b
r
.
( )
,a b
r r
=90
0
⇔
a
r
vuông góc
b
r
.
( )
,a b
r r
tuỳ ý n u ế
a
r
ho c ặ
b
r
là
0
r
.
II/TÍCH VÔ H NG C A HAI VECT :ƯỚ Ủ Ơ
1.Đ NH NGHĨA:ỊTích vô h ng c a hai vect ướ ủ ơ
a
r
,
b
r
là 1 s .KH: ố
a
r
.
b
r
.
Tính theo công th c: ứ
( )
. cos ,a b a b a b=
r r r r r r
.
Tích vô h ng ướ
.a a
r r
đ c g i là bình ph ng vô h ng c aượ ọ ươ ướ ủ
a
r
.KH:
2
a
r
.
Ta có:
2
20
. cos0a a a a a a= = =
r r r r r r
2.CHÚ Ý:
( )
,a b
r r
=00
⇔
a
r
.
b
r
=
a b
r r
.
( )
,a b
r r
=180
0
⇔
a
r
.
b
r
=-
a b
r r
.
( )
,a b
r r
=90
0
⇔
a
r
.
b
r
=0.
3.VÍ D :ỤCho tam giác ABC đ u c nh a. ề ạ
Tính:
. , .AB AC AC CB
uuur uuur uuur uuur
.
Gi i:ả
( )
2
0
. cos , . .cos60 2
a
AB AC AB AC AB AC a a= = =
uuur uuur uuur uuur uuur uuur
Trang 4
( )
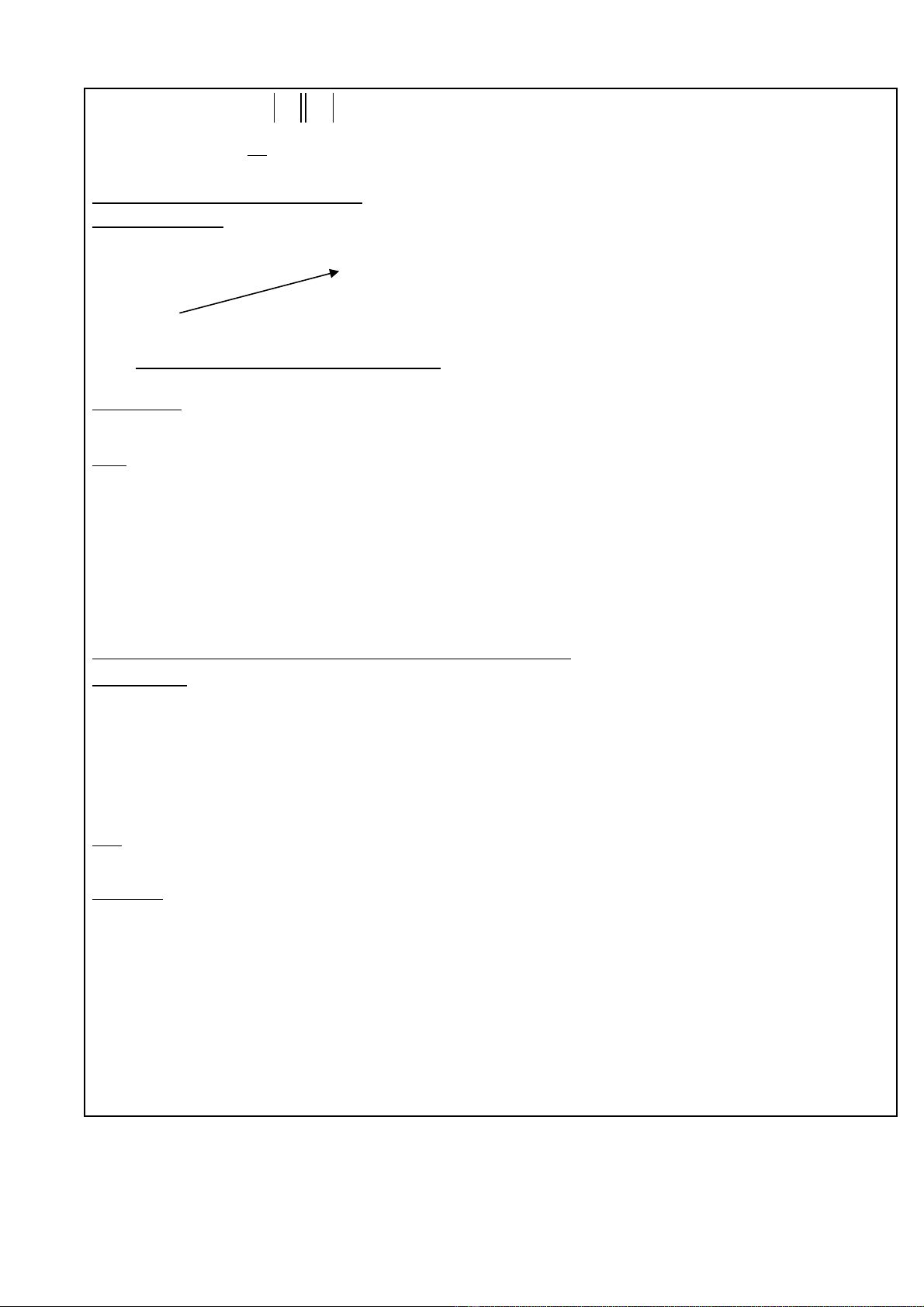
2
0
. . cos ,
. .cos60 2
AC CB CA CB CA CB CA CB
a
a a
= − = − =
= − = −
uuur uuur uuuruuur uuur uuur uuur uuur
III/CÔNG TH C HÌNH CHI U:Ứ Ế
1)Đ NH NGHĨA:Ị Cho
a AB=
r uuur
và đ ng th ng d.G i A’,B’ là hình chi u c a A và B trên d.Khi đóườ ẳ ọ ế ủ
' ' 'a A B=
r uuuur
g i là hình chi u c a ọ ế ủ
a
r
trên d.
d
2.Đ NH LÝỊ:Tích vô h ng c a hai vect ướ ủ ơ
,a b
r r
b ng tích vô h ng c a ằ ướ ủ
a
r
và hình chi u c a ế ủ
b
r
trên
đ ng th ng ch a ườ ẳ ứ
a
r
.
CM:Trên đ ng th ng ch a vect ườ ẳ ứ ơ
a
r
l y đi m O,d ng ấ ể ự
,OA a OB b= =
uuur r uuur r
.G i B’ là HC c a B trênọ ủ
đ ng th ng ch a OA.ườ ẳ ứ
Khi đó
'OB
uuuur
là hchi u c a ế ủ
OB b=
uuur r
trên đ ng th ng ch a ườ ẳ ứ
a
r
.
Ta có
( )
·
,OA OB AOB
ϕ
= =
uuur uuur
Th1:
0
90
ϕ
<
Th2:
0
90
ϕ
≥
IV/ CÁC TÍNH CH T C B N C A TÍCH VÔ H NG:Ấ Ơ Ả Ủ ƯỚ
1.Đ NH LÝ:Ị
V i m i vect ớ ọ ơ
, ,abc
r r r
và m t s k ta có:ộ ố
) . .i a b b a=
r r r r
(Giao hoán)
( )
) . . .ii a b c a b a c+ = +
r r r r r r r
(Phân ph i)ố
( ) ( )
) . .iii ka b k a b=
r ur r r
(K t h p)ế ợ
CM:SGK.
2.VÍ D :Ụ
1.CM:
( )
22 2
2 .a b a b a b+ = + +
r r r r r r
Gi i: ả
( ) ( ) ( ) ( )
VT a b a b a a b b a b= + + = + + +
r r r r r r r r r r
2 2
. . . . 2 .a a a b b a b b a b a b= + + + = + +
r r r r r r r r r r r r
4.Cho tam giác cân đ nh A và đ ng cao AH.G i D là hchi u vuông góc c a H trên Ac,M là trung đi mỉ ườ ọ ế ủ ể
HD. CMR:
AM BD⊥
.
Gi i:ả
Trang 5