Đ
Ề KIỂM TRA 1 TIẾT HK2
MÔN: Toán 9
ĐỀ 13
Đề bài: Câu 1(2đ)
a. Cho tứ giác ABCD nội tiếp đường tròn (0), biết  = 520,
D
= 1120. Tính số đo của góc
C và góc B.
b. Hai tiếp tuyến tại A và tại B của đường tròn (O;R) cắt nhau ở M. Biết OM = 2R. Tính
số đo của góc ở tâm AOB?
Câu 2 ( 3 đ). Cho đườnh tròn (O), bán kính R = 4cm, số đo của cung AmB = 600.
a. Tính độ dài đường tròn và diện tích hình tròn nói trên.
b. Tính độ dài cung nhỏ AmB và điện tích hình quạt tròn OAmB.
c. Tính diện tích hình viên phân AmB.
Câu 3(1 đ) Dựng ABC, biết AB = 3cm, C = 600 , đường cao CH = 2 cm.
Câu 4 (4 đ) Cho ABC vuông tại A. Trên AC lấy một điểm M và vẽ đường tròn đường
kính MC. Kẻ BM cắt đường tròn tại D. Đường thẳng DA cắt đường tròn tại S. chứng
minh rằng:
a. ABCD là một tứ giác nội tiếp.
b. CA là tia phân giác của góc SCB
c. Từ B kẻ tiếp tuyến BN với đường tròn (N là tiếp điểm). Chứng minh BN2
=BM.BD
ĐÁP ÁN VÀ THANG ĐIỂM
Đáp án này gồm 02 trang
CÂU Ý Nội dung Điểm
Câu 1
2đ a Do tứ giác ABCD nội tiếp đường tròn (0).
Nên
A
+
C
= 1800
Do đó
C
= 1800 -
A
Thay số
C
= 1800 - 520 = 1280.
Ta lại có
B
+
D
= 1800
Suy ra
B
= 1800 -
D
Thay số
B
= 1800 - 1120 = 680.
1đ
b Do MA là tiếp tuyến của đường tròn (O). Nên MA
OA tại A
hay
AOM
= 900.
Ta có cos
AOM
=
1
R
R
OM
OA
Suy ra
AOM
= 600.
Ta có OM là tia phân giác của
AOB
Nên
AOB
= 2
AOM
= 1200.
Vậy góc ở tâm AOB bằng 1200.
1đ
Câu 2
3đ
a Tính C = 2
R =2
.4cm = 8
(cm).
S = R2 = . 42 = 16 (cm2).
0,5 đ
0,5 đ
b Do sđ
AmB
= 600 nên n = 600
Độ dài cung nhỏ AmB là :
4
3
(cm).
Diện tích hình quạt tròn OAmB là:
8
3
. (cm2).
0,5 đ
0,5 đ
c Do AOB đều cạnh R nên 2. 3 16. 3
4 3
4 4
AOB
R
S (cm2).
Diện tích hình viên phân AmB là: Sq - S ∆AOB 1,45 (cm2).
0,5 đ
0,5 đ
Câu 3 1đ Dựng
ABC thỏa mãn yêu cầu 1đ
Câu 4
4 đ
a Câu 4 (4 đ) Cho
ABC vuông tại A. Trên AC lấy một điểm M và vẽ
đường tròn đường kính MC. Kẻ BM cắt đường tròn tại D. Đường thẳng
DA cắt đường tròn tại S. chứng minh rằng:
a. ABCD là một tứ giác nội tiếp.
b. CA là tia phân giác của góc SCB
c. Từ B kẻ tiếp tuyến BN với đường tròn (N là tiếp điểm). Chứng
minh BN2 =BM.BD
1,5 đ
O
A
m
B
SD
M
C
B
A
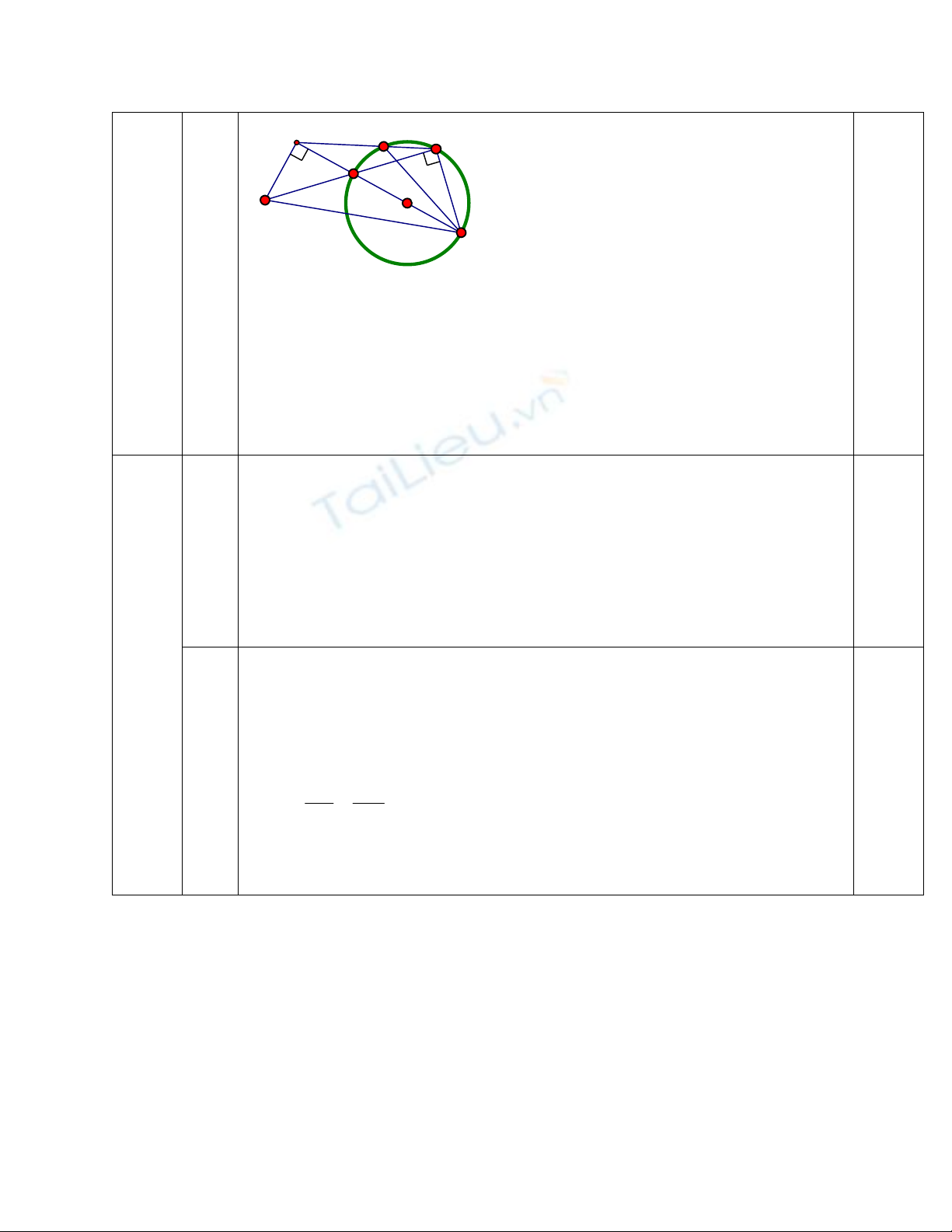
Vẽ hình 0,5 đ
a). Ta có:
BAC
= 900 ( góc nội tiếp chắn nửa đường tròn )
Ta lại có:
BDC
=
MDC
= 900 ( MDC chắn nửa đường tròn đường kính
MC)
Do 2 điểm A và D cùng nhìn đoạn BC dưới một góc vuông nên các điểm A,
B, C, D nằm trên đường tròn đường kính BC.
Vậy ABCD là một tứ giác nội tiếp.
b Chứng minh : CA là tia phân giác của góc SCB.
Trong đường tròn ngoại tiếp ABCD ta có:
ADB = SDM = ACB
(các góc nội tiếp cùng chắn
AB
) (1)
Trong đường tròn đường kính CM ta có:
SDM = SCM
(các góc nội tiếp cùng chắn
SM
) (2)
Từ (1) và (2) ta có:
SCM=SCA=ACB
và CA nằm giữa hai tia CB và CS
Vậy CA là tia phân giác của góc SCB
0,5đ
0,5đ
0,5đ
c Kẻ tiếp tuyến BN với đường tròn.
Xét ∆BNM và ∆ BMD có:
B
chung
BNM BDN
(cùng chắn cung NM).
Nên ∆BNM ∽∆ BMD
Do đó:
BN BM
BD BN
Suy ra : BN2 =BM.BD
0.5đ
0.5đ