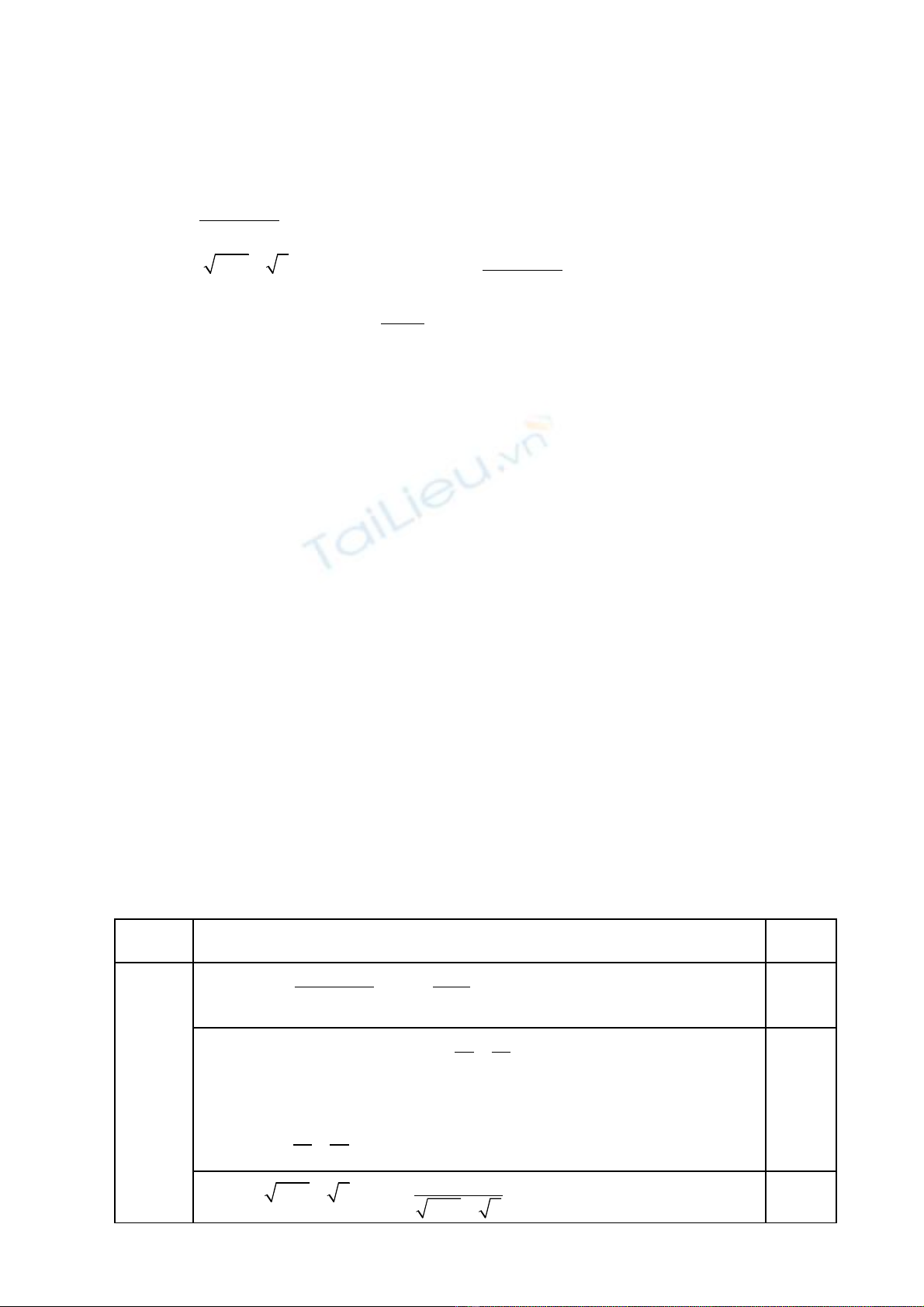
Đ thi h c kì II:ề ọ
Môn: Toán……
L p 11 Nâng caoớ
-------------****--------------
Đ : ề
Câu 1: (2đ) Tìm gi i h n c a các hàm s sau:ớ ạ ủ ố
a)
2
1
1
3 2
lim
x
x
x x
→−
+
+ +
b)
4 2
( 3 1)
lim
x
x x
→+∞
+ −
c)
( 1 )
lim
x
x x
→+∞
+ −
d)
2
2
5 6
lim
x
x
x x
+
→−
+ +
Câu 2: (1,5đ) Cho hàm s : ố
3
2, 2
( ) 8
3, 2
xx
f x x
a x
−
≠
=−
− =
a) Tính
2
( )
lim
x
f x
→
b) Tìm a đ hàm s liên t c trên ể ố ụ R.
Câu 3: (2đ) Cho hàm s ố
3 2
( ) 5f x x x x= + −
a) Tính đ o hàm c a hàm s trên R.ạ ủ ố
b) b) Gi i b t ph ng trình ả ấ ươ
'( ) 0f x ≤
c) Vi t ph ng trình ti p tuy n c a đ th hàm s ế ươ ế ế ủ ồ ị ố y=f(x) t i đi m có hoành đ b ng -5. ạ ể ộ ằ
Câu 4: (1,5đ) Cho hàm s ốf(x)=sinx(1+cosx).
a) Tính đ o hàm c a hàm s trên R. ạ ủ ố
b) Gi i ph ng trình f’(x)=0. ả ươ
Câu 5:(3đ) Cho hình chóp S.ABCD, ABCD là hình vuông c nh a,ạ
,
góc SBA b ng 30ằ0.
a) Ch ng minh SBC là tam giác vuông. ứ
b) Ch ng minh ứ
( ) ( )SAB SAD⊥
c) Tính kho ng cách gi a hai đ ng th ng SD và ABả ữ ườ ẳ .
d) G i M, N l n l t là trung đi m c a BC và DC. Tính góc gi a hai m t ph ng (SAN),ọ ầ ượ ể ủ ữ ặ ẳ
(SAM).
----------------------------------------------------------------------------------------------------------------
ĐÁP ÁN VÀ THANG ĐI M:Ể
Câu Đáp án Thang
đi mể
Câu 1
(2đ) a)
2
1 1
1 1 1
3 2 2
lim lim
x x
x
x x x
→− →−
+= =
+ + +
0.5đ
b)
4 2 4
2 4
3 1
( 3 1) (1 )
lim lim
x x
x x x x x
→+∞ →+∞
+ − = + − = +∞
(vì
4
2 4
3 1
(1 ) 1 0
lim
lim
x
x
x
x x
→+∞
→+∞
= +∞
+ − = >
)
0.5đ
c)
1
( 1 ) 0
1
lim lim
x x
x x x x
→+∞ →+∞
+ − = =
+ +
0.5đ
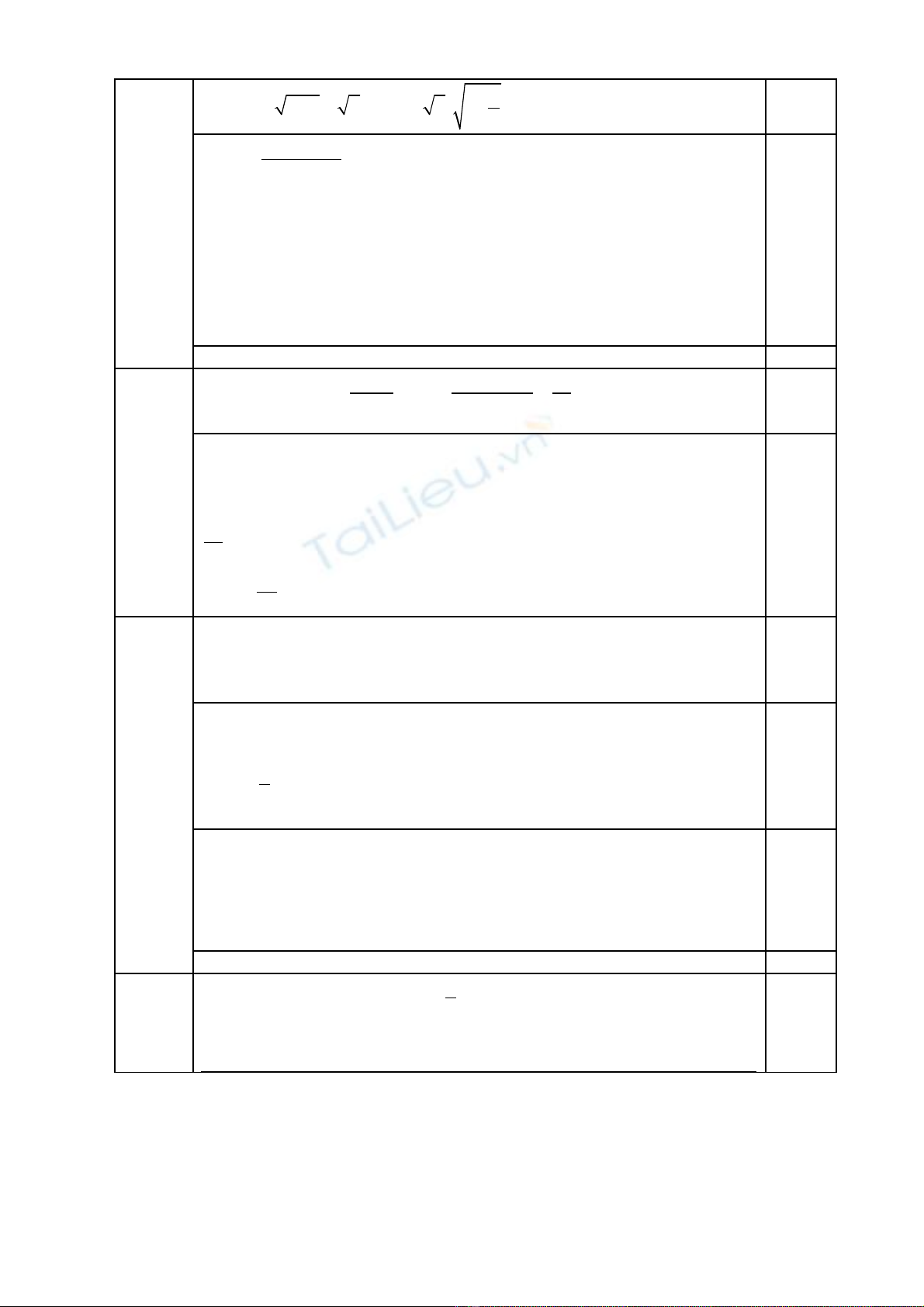
(vì
1
( 1 ) ( 1 1)
lim lim
x x
x x x x
→+∞ →+∞
+ + = + + = +∞
)
d)
2
2
2
2
2
2
,
5 6
2 0,
( 5 6) 0,
5 6 0, 2
lim
lim
lim
x
x
x
x
x x
x
x x
x x x
+
+
+
→−
→−
→−
= −∞
+ +
= − <
+ + =
+ + > ∀ > −
0.5đ
Câu 2
(1.5đ) a)
3 2
2 2 2
2 1 1
( ) 8 2 4 12
lim lim lim
x x x
x
f x x x x
→ → →
−
= = =
− + +
0,75đ
b) Hàm s f(x) liên t c trên kho ng ố ụ ả
( ; 2) (2; )−∞ ∪ +∞
Hàm s liên t c trên R khi và ch khi hàm s liên t c t i x=2ố ụ ỉ ố ụ ạ
2
( ) (2)
lim
x
f x f
→
⇔ =
13
12
37
12
a
a
= −
⇔ =
0,25đ
0,5đ
Câu 3
(2đ)
3 2
( ) 5f x x x x= + −
a)
2
'( ) 3 2 5f x x x= + −
0,5đ
b)
2
'( ) 0
3 2 5 0
51
3
f x
x x
x
≤
⇔ + − ≤
⇔ − ≤ ≤
S=[-5/3; 1 ]
0.75đ
d) Ph ong trình ti p tuy n có d ng: ư ế ế ạ
'( 5)( 5) ( 5)
60( 5) 75
60 225
y f x f
y x
y x
= − + + −
⇔ = + −
⇔ = +
0.75đ
Câu 4
(1,5đ) a)
1
( ) sinx+sinx.cosx=sinx+ sin 2
2
'( ) osx+cos2x
f x x
f x c
=
⇒ =
0.75đ
b)
2
'( ) 0
osx+cos2x=0
cosx+2cos 1 0
osx=-1
1
cosx= 2
f x
c
x
c
=
⇔
⇔ − =
⇔
2
2
3
x k
x k
π π
ππ
= +
= ± +
0.5đ
0.25đ
Câu 5
(3đ)
H
N
M
C
A
B
S
0,25đ
a)
( )
( )
SA ABCD SA BC
BC AB
BC SAB
BC SB
⊥ ⇒ ⊥
⊥
⇒ ⊥
⇒ ⊥
Suy ra tam giác SBC là tam giác vuông t i B.ạ
0.75đ
b)
( )
AB SA AB SAD
AB AD
⊥
⇒ ⊥
⊥
mà
( )
( ) ( )
AB SAB
SAB SAD
⊂
⇒ ⊥
0.5đ
c) Trong m t ph ng (SAD), k AH vuông góc v i SD.ặ ẳ ẻ ớ
Ta có
( )SA SAD SA AH⊥ ⇒ ⊥
Suy ra:
( , )d AB SD AH=
Trong tam giác SAB, ta có:
0
tan( ) .tan 30 3
SA a
SBA SA AB
AB
= ⇒ = =
Trong tam giác SAD, ta có:
2 2 2 2 2 2
1 1 1 1 3 4
2
AH AD SA a a a
a
AH
= + = + =
⇒ =
0.75đ
V y kho ng cách gi a hai đ ng th ng AB và SD là a/2.ậ ả ữ ườ ẳ
d) Ta có:
( ) ( )
( )
( ) ( )
( ) ( )
SAN SAM SA
SA ABCD
ABCD SAN AN
ABCD ABM AM
⊥ =
⊥
∩ =
∩ =
Suy ra góc gi a hai m t ph ng (SAN) và (SAM) là góc gi a haiữ ặ ẳ ữ
đ ng th ng AM và AN.ườ ẳ
5
2
a
AM AN= =
2
2 2
DB a
MN = =
Trong tam giác AMN:
2 2 2
AN 4
ˆ
osMAN= 2 . 5
4
ˆarccos 5
AM MN
cAM AN
MAN
+ − =
⇒ =
V y góc gi a hai m t ph ng (SAN) và (SAM) b ng arccos(4/5).ậ ữ ặ ẳ ằ
0,25đ
0.5đ