KỲ THI TOÀN QUỐC GIẢI TOÁN TRÊN MÁY TÍNH CASIO NĂM 2009
MÔN: TOÁN 12 (THPT)
THỜI GIAN: 150 PHÚT
NGÀY THI: 13/03/2009
Câu 1: Tính nghiệm giá trị của hàm số sau tại
0,5x
:
3
2
2 sin 1
() ln( 3)
xx
fx xx


Câu 2: Tìm tọa độ giao điểm của của đồ thị hai hàm số
2
75y x x
và
2
8 9 11
1
xx
yx

Câu 3: Viết phương trình các tiếp tuyến của đồ thị hàm số
32
42y x x x
đi qua
điểm
(1; 4)A
Câu 4: Tính gần đúng giá trị lớn nhất và giá trị nhỏ nhất của hàm số:
1 5 2y x x
Câu 5: Tính gần đúng nghiệm của hệ phương trình:
2 3 7
4 9 25
xy
xy


Câu 6: Cho dãy số
có
1 2 3
1; 2; 3u u u
và
1 2 3
2 3 ( 4)
n n n n
u u u u n
.
Tính
20
u
Câu 7: Tìm nghiệm gần đúng của phương trình:
3
3 5 7 (log 1)
x x x x
.
Câu 8: Tính diện tích hình tứ giác ABCD biết
4 , 4 , 5AB cm BC cm CD cm
,6DA cm
và góc
70o
B
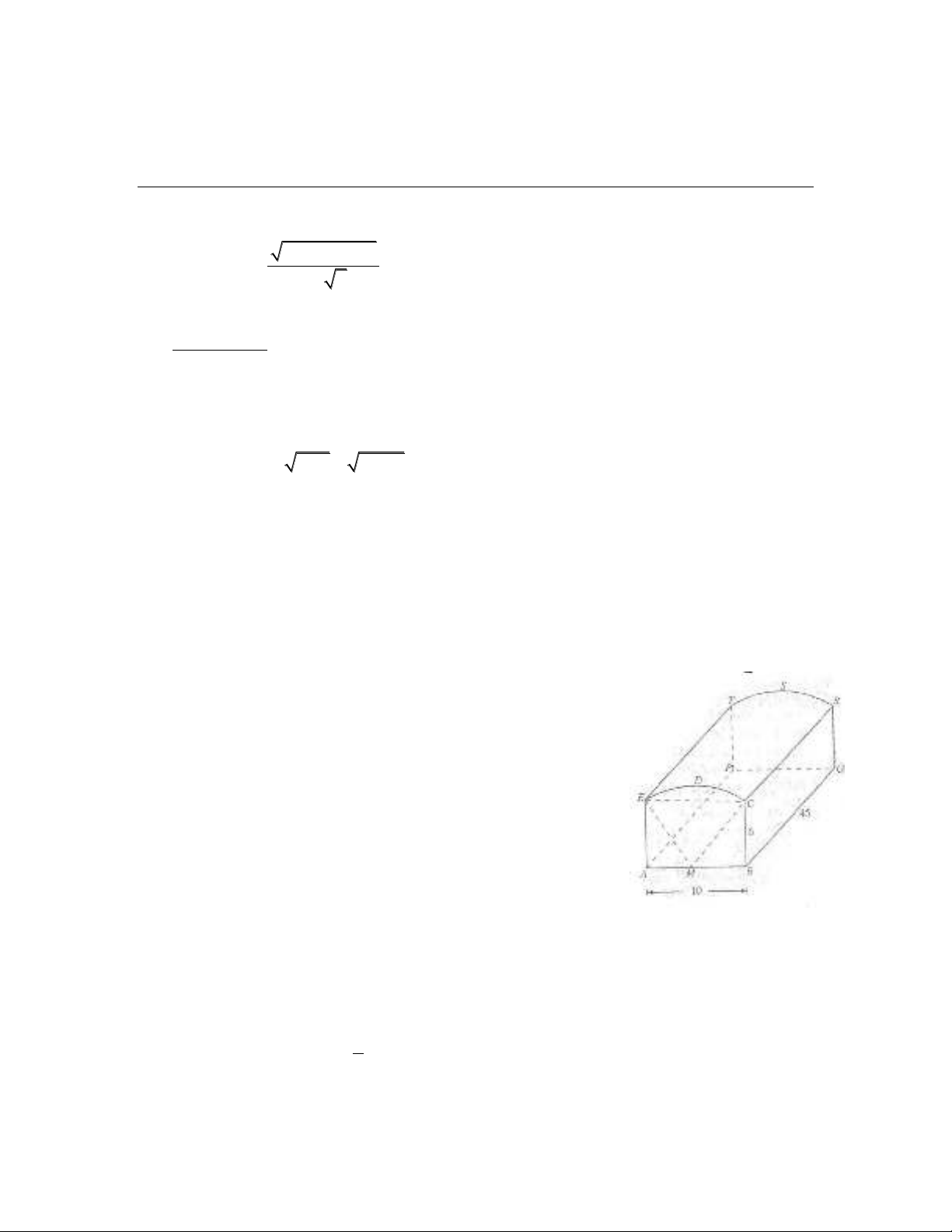
Câu 9: Một hộp nữ trang ( xem hình vẽ) có mặt bên
ABCDE với ABCE là hình chữ nhật, cạnh cong CDE
là một cung của đường tròn tâm tại trung điểm M của
cạnh AB. AB = 10cm, BC = 6cm và BQ = 45cm. Hãy tính:
1. Góc CME theo radian.
2. Độ dài cung CDE
3. Diện tích hình quạt MCDE
4. Diện tích toàn phần của hộp nữ trang.
5. Thể tích của hộp nữ trang.
Câu 10: Với việc tính toán trên máy thì thời gian thực hiện các phép tính nhan và chia
lớn gấp bội so với thời gian thực hiện các phép tính cộng và trừ. Cho nên, một tiêu chí để
đánh giá tính hiệu quả của một công thức ( hay thuật toán ) là ở chỗ cho phép sử dụng ít
nhất có thể các phép tính nhân và chia
Với số
e
, người ta có thể tính xấp xỉ nó theo công thức sau đây:
1
1
lim
n
n
en





(1)
0
1
!
n
en
(2)
Theo em, để tính được giá trị của biểu thức
1025
1
11025
A



thì cần tới bao
nhiêu phép nhân và chia, và khi ấy kết quả thu được xáp xỉ số
e
chính xác tới bao nhiêu
chữ số thập phân sau dấu phẩy.
Câu hỏi tương tự như trên đối với biểu thức
6
0
1
!
n
Bn
.
KỲ THI TOÀN QUỐC GIẢI TOÁN TRÊN MÁY TÍNH CASIO NĂM 2009
MÔN: TOÁN 9 (THCS)
THỜI GIAN: 150 PHÚT
NGÀY THI: 13/03/2009
Câu 1: Tính giá trị của biểu thức
a) A =
2 3 4
4
23
1,25 15,37 3,75
1 3 2 5 2
4 7 5 7 3





b) B =
3 5 3 5 2009 13,3
3 2 5 3 7 2 3 5 4 7
c) C =
3 2 2 3 2 3
3 2 2 3 2 3
(1 sin 17 34`) (1 25 30`) (1 cos 50 13`)
(1 cos 35 25`) (1 cot 25 30`) (1 sin 50 13`)
tg
g
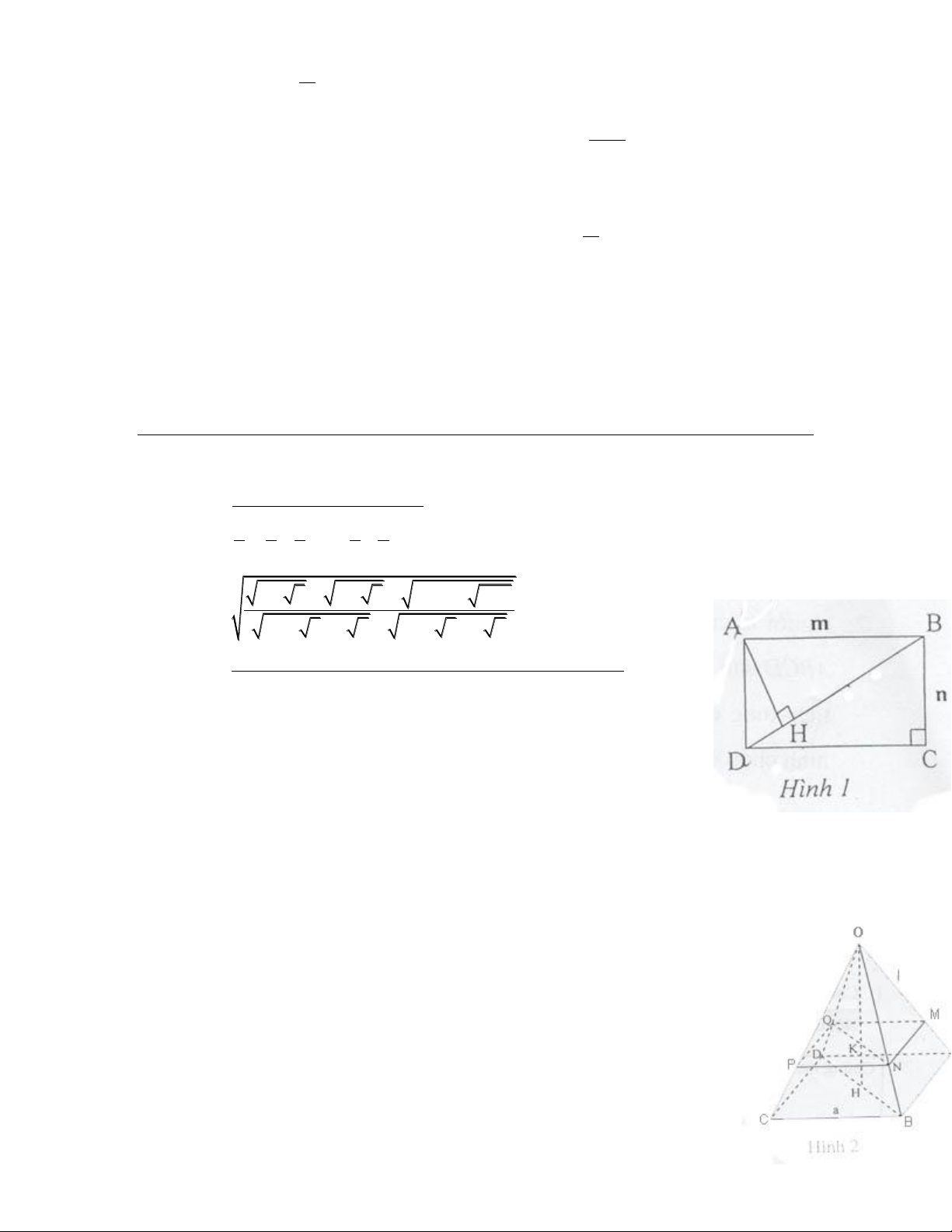
Câu 2: Hình chữ nhật ABCD có độ dài các cạnh AB = m, BC = n.
Từ A kẻ AH vuông góc với đường chéo BD
a) Tính diện tích tam giác ABH theo m, n
b) Cho biết m = 3,15 cm và n = 2,43 cm.
Tính ( chính xác đến 4 chữ số thập phân) diện tích tam giác ABH
Câu 3: Đa thức
6 5 4 3 2
()P x x ax bx cx dx ex f
có giá trị là 3; 0; 3; 12; 27; 48
khi x lần lượt nhận giác trị là 1; 2; 3; 4; 5; 6
a) Xác định các hệ số a, b, c, d, e, f của P(x)
b) Tính giá trị của P(x) với x = 11; 12; 13; 14; 15; 16; 17; 18; 19; 20
Câu 4:
1. Hình chóp tứ giác đều
. O ABCD
có độ dài cạnh đáy
BC a
,
độ dài cạnh bên
OA l
a) Tính diện tích xung quanh, diện tích toàn phần và thể tích của
hình chóp
. O ABCD
theo
a
và
l
.
b) Tính ( chính xác đến 2 chữ số thập phân) diện tích xung quanh
và thể tích của hình chóp
. O ABCD
khi cho biết
5,75 , 6,15a cm l cm
2. Người ta cắt hình chóp
. O ABCD
cho trong câu 1 bằng mặt phẳng
song song với đáy
ABCD
sao cho diện tích xung quanh của hình chóp
.O MNPQ
được cắt ra bằng diện tích xung quanh của hình chóp cụt đều
.MNPQ ABCD
được cắt ra. Tính thể tích hình chóp cụt được cắt ra
( chính xác đến 2 chữ số thập phân )
Câu 5:
1. Một chiếc thuyền khởi hành từ một bến sông A. Sau 5 giờ 10 phút, một chiếc
canô chạy từ A đuổi theo và gặp thuyền đó cách bến A 20,5 km. Hỏi vận tốc của
thuyền, biết rằng canô chạy nhanh hơn thuyền
12,5 /km h
. ( Kết quả chính xác với
2 chữ số thập phân)
2. Lức 8 giờ sáng, một ô tô đi từ A đến B, đường dài 157 km. Đi được 102 km thì xe
bị hỏng máy phải dừng lại sửa chữa mất 12 phút rồi đi tiếp đến B với vận tốc ít
hơn lúc đầu là
10,5 /km h
. Hỏi ô tô bị hỏng lúc mấy giờ, biết rằng ô tô đến B lúc
11 giờ 30 phút. ( Kết quả thời gian làm tròn đến phút)
Câu 6: Cho dãy số
1 2 1 2
22
nn
n
U
với n =1,2,…,k,….
1. Chứng minh rằng:
11
2
n n n
U U U


với
1n
2. Lập quy trình bấm phím liên tục tính
theo
n
U
và
với
12
1, 2UU
3. Tính các giá trị từ
11
U
đến
20
U
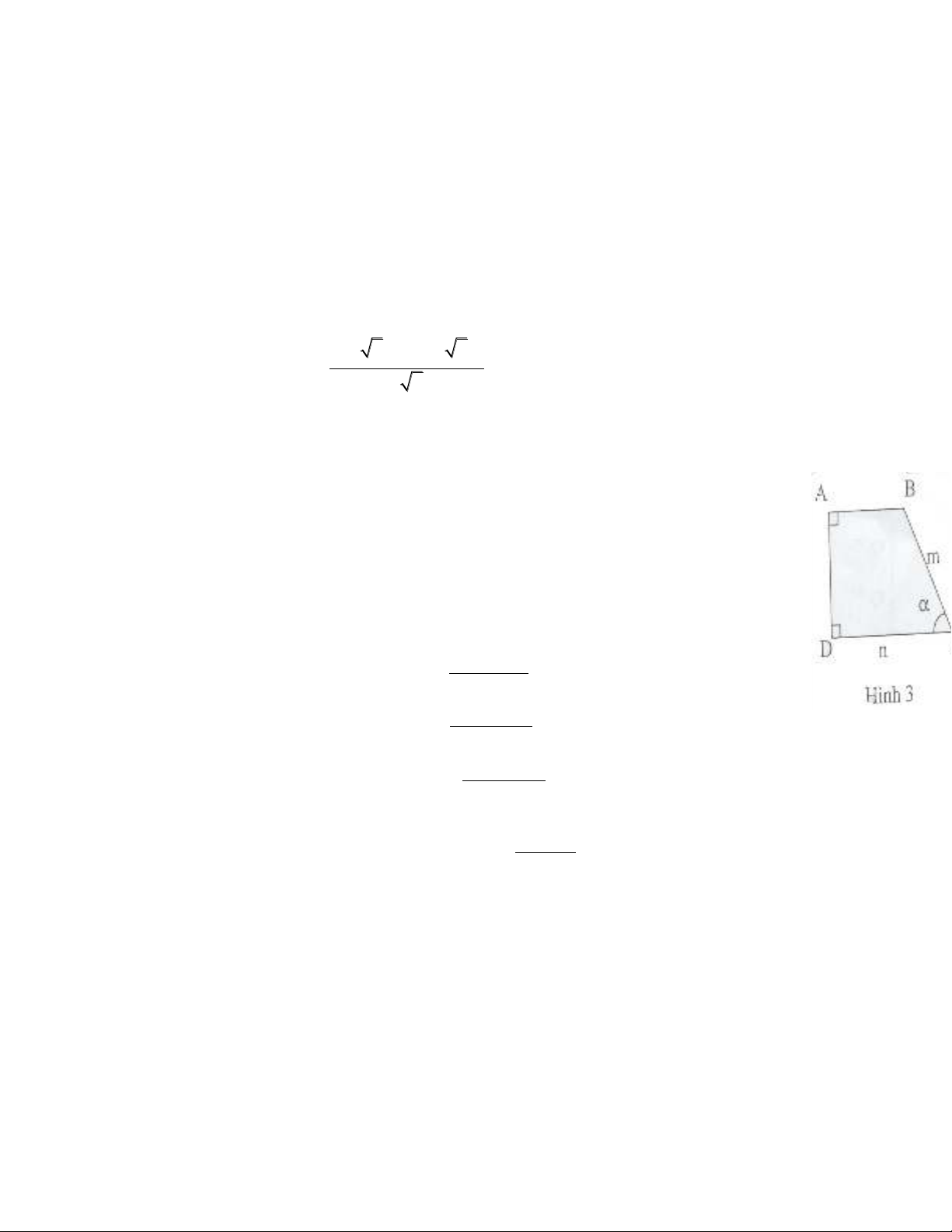
Câu 7: Hình thang vuông
( // )ABCD AB CD
có góc nhọn
BCD
,
độ dài các cạnh
,BC m CD n
a) Tính diện tích, chu vi và các đường chéo của hình thang
ABCD
theo
và
.
b) Tính ( chính xác đến 4 chữ số thập phân ) diện tích, chu vi và các
đường chéo của hình thang
ABCD
với
,
4,25 , 7,56 , 54 30
o
m cm n cm
Bài 8:
1. Số chính phương
P
có dạng
17712 81P ab
. Tìm các chữ số
,ab
biết rằng
13ab
2. Số chính phương
Q
có dạng
15 26849Q cd
. Tìm các chữ số
,cd
biết rằng
22
58cd
3. Số chính phương
M
có dạng
1 399025M mn
chia hết cho 9. Tìm các chữ số
Bài 9: Cho dãy số xác định bởi công thức :
2
12
3 13
1
n
n
n
x
xx
với
10,09x
, n = 1,2,3,…,
k,…
a) Viết quy trình bấm phím liên tục tính
1n
x
theo
n
x
.
b) Tính
23456
, , , ,x x x x x
( với đủ 10 chữ số trên màn hình )
c) Tính
100 200
,xx
( với đủ 10 chữ số trên màn hình )
Bài 10: Cho tam giác
ABC
vuông tại
A
. Từ A kẻ AH vuông góc với BC ( H thuộc BC )
Tính độ dài cạnh AB ( chính xác đến 2 chữ số thập phân), biết rằng diện tích tam
giác AHC là
2
4,25S cm
, độ dài cạnh AC là
5,75m cm
.
KỲ THI TOÀN QUỐC GIẢI TOÁN TRÊN MÁY TÍNH CASIO NĂM 2009
MÔN: TOÁN 12 (THBT)
THỜI GIAN: 150 PHÚT
NGÀY THI: 13/03/2009
Quy ước: Khi tính gần đúng chỉ lấy kết quả với 4 chữ số thập phân, riêng số đo góc thì
lấy đến số nguyên giây.
Bài 1: Tính gần đúng (độ, phút, giây) của phương trình:
2
2sin2 5sin 1xx
Bài 2: Tính gần đúng giá trị lớn nhất và giá trị nhỏ nhất của hàm số: f(x) =
2
3 4 5 2xx
Bài 3: Khi sản xuất vỏ lon sữa bò hình trụ, các nhà thiết kế luôn đặt mục tiêu sao cho chi
phí nguyên liệu làm vỏ lon là ít nhất, tức là diện tích toàn phần của hình trụ là nhỏ nhất.
Tính gần đúng diện tích toàn phần của lon khi ta muốn có thể tích của lon là 1
3
dm
.
Bài 4: Tính gần đúng giá trị cực tiểu và giá trị cực đại của hàm số
2
2 5 3
21
xx
yx

Bài 5: Tính gần đúng nghiệm của hệ phương trình:
2
3
3
log 9 8
log 3 2
y
y
x
x


Bài 6: Tính gần đúng giá trị của a và b nếu đường thẳng y = ax + b đi qua điểm M (1;2)
và là tiếp tuyến của đồ thị hàm số
2
3 4 5y x x
Bài 7: Tính gần đúng bán kính R của mặt cầu ngoại tiếp hình tứ diện ABCD có các cạnh
AB = AC = AD = 8dm, BC = 7dm, CD = 6dm, BD = 5dm.
Bài 8: Tính a, b, c nếu đồ thị hàm số
32
y x ax bx c
đi qua ba điểm A( 5;1), B(6;2),
C(7;3).
Bài 9: Tính gần đúng thể tích khối chóp S.ABCD nếu đáy ABCD là hình bình hành, cạnh
SA vuông góc với đáy, AB = 7dm, AC = 9dm, SD = 11dm, góc ABC =
80o
.
Bài 10: Tính gần đúng tọa độ giao điểm của elip :
22
1
94
xy

và đường thẳng
5 6 7 0xy
SỞ GIÁO DỤC –ĐÀO TẠO KỲ THI LẬP ĐỘI TUYỂN HỌC SINH GIỎI
TỈNH BÀ RỊA –VŨNG TÀU LỚP 12 DỰ THI QUỐC GIA, NĂM HỌC 2010-2011
MÔN THI: TOÁN
Thời gian làm bài thi 180 phút
Ngày thi: 07/12/2010
Câu 1( 4 điểm )
a/ Giải phương trình: 2
2( 1)(1 1)
x x x x x
.
b/ Giải bất phương trình: 2
3 2
log ( 2 1) 1 log
x x x
.
Câu 2( 4 điểm )
Cho tam giác ABC vuông ở A và nội tiếp trong đường tròn (O) .Trên tia đối của các tia
BA, CA ta lấy các điểm E và F sao cho BE = CF = BC . M là điểm chạy trên (O).
Chứng minh rằng : MA + MB + MC
EF.
Câu 3( 4 điểm ) Cho dãy số (un) thỏa :
1
3 *
1
1 1 61
;
4 8
15 ,
64
n n
u
u u n N
a) Chứng minh dãy số (un) có giới hạn.
b) Tìm
lim
n
u
.
Câu 4( 3 điểm )
Tìm tất cả các hàm số
:[0; ) [0; )
f
 
, thoả mãn:
( ( )) ( ( )) 2( ( ) 3 ); , 0
f x f y f y f x f y x y x y
.
Câu 5( 5 điểm )
a) Tìm tất cả các số chính phương gồm 4 chữ số sao cho 2 chữ số đầu giống nhau, 2 chữ
số cuối giống nhau và khác không?
b) Trên mặt phẳng cho 2 x 2010 điểm ; trong đó không có bất kì 3 điểm nào thẳng
hàng.Người ta tô 2010 điểm bằng màu đỏ và tô 2010 điểm còn lại bằng màu xanh.
Chứng minh rằng:bao giờ cũng tồn tại một cách nối tất cả các điểm màu đỏ với tất cả
các điểm màu xanh bởi 2010 đoạn thẳng không có điểm nào chung.
---------------------------------------------------------HẾT-----------------------------------------------