
PHẦN CHUNG CHO TẤT CẢ THÍ SINH (7,0 điểm)
Câu 1. (2,0 điểm)
Cho hàm số 4 2 2
2
y x mx m m
(1)
1.Khảo sát sự biến thiên và vẽ đồ thị hàm số (1) khi m = -2
2.Tìm m để đồ thị hàm số (1) có ba điểm cực trị tạo thành một tam giác có một góc bằng 1200
Câu 2. (1,0 điểm) Tìm nghiệm x thuộc khoảng
(0; )
của phương trình
2 2
3
4sin ( ) 3 sin( 2 ) 1 2 os ( )
2 2 4
xx c x
.
Câu 3. (1,0 điểm) Giải hệ phương trình
2 2 2 2
2
( )( 3) 3( ) 2
4 2 16 3 8
x y x xy y x y
x y x
,x y
Câu 4. (1,0 điểm)Tính: 3
4 2
3
5 6
x x
I dx
x x
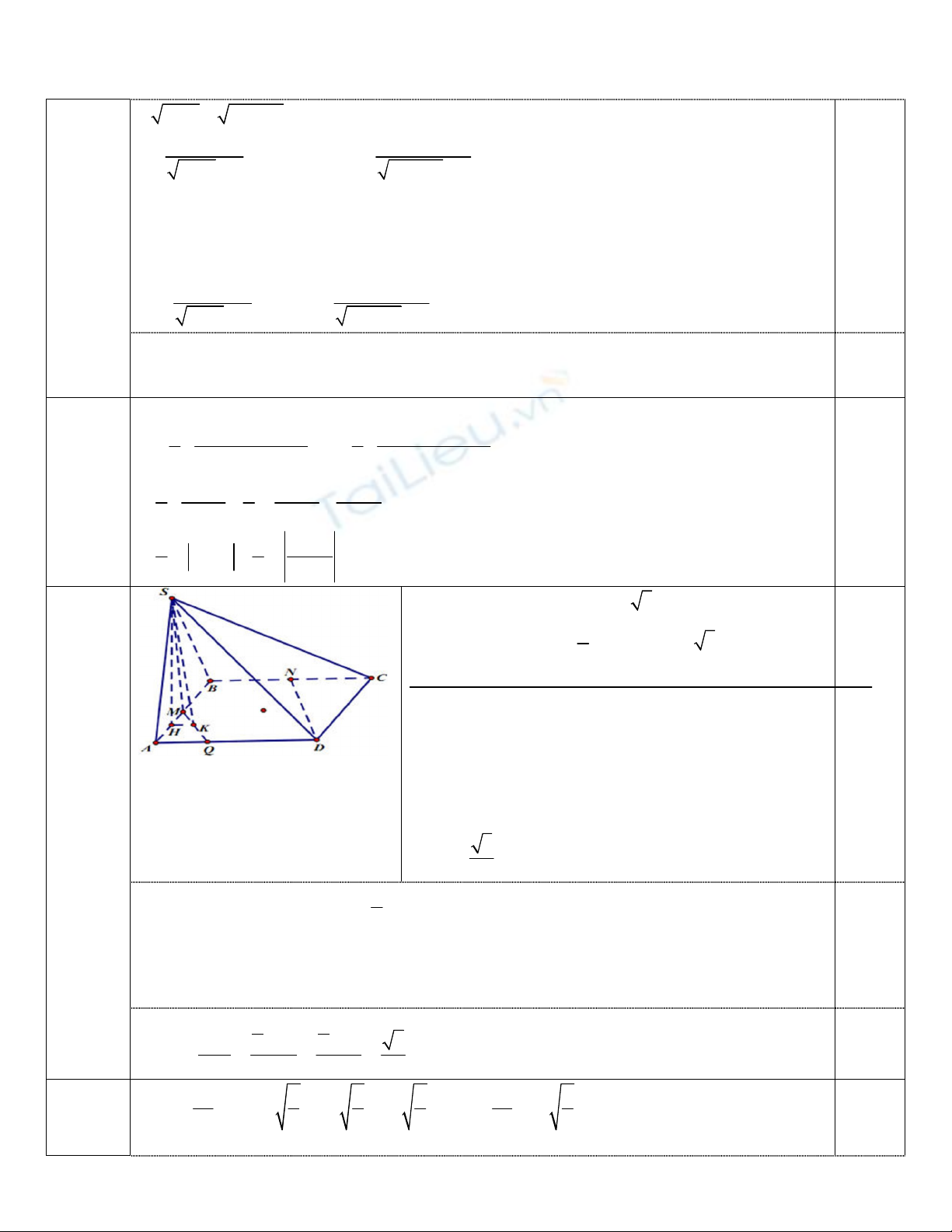
Câu 5. (1,0 điểm) Cho hình chóp S.ABCD đáy là hình thoi cạnh 2a,SA = a,
SB = a
3
,gócBAD bằng 600,
SAB ABCD
,gọi M,N lần lượt là trung điểm AB và BC. Tính
thể tích khối chóp S.ABCD và cosin giữa hai đường thẳng SM và DN.
Câu 6. (1,0 điểm) Cho các số dương a, b, c thỏa mãn
3
abc
Chứng minh rằng:
3
a b c
b c a
.
PHẦN RIÊNG (3,0 điểm): Thí sinh chỉ được làm một trong hai phần( A hoặc B)
A. Theo chương trình Chuẩn
Câu 7.a (2,0 điểm)
1.Trong mặt phẳng Oxy, cho tam giác ABC có AB=
5
, C(-1;-1), phương trình cạnh AB là:
x-2y-3=0, trọng tâm G thuộc đường thẳng: x+y-2=0. Tìm tọa độ các đỉnh A, B.
2.Trong mặt phẳng Oxy, cho đường tròn (C1):
2 2
13
x y ,đường tròn (C2):
2 2
( 6) 25
x y .
Gọi giao điểm có tung độ dương của (C1) và (C2) là A,viết phương trình đường thẳng đi qua
A,cắt (C1) và (C2) theo hai dây cung có độ dài bằng nhau
Câu 8.a (1,0 điểm) Có 12 học sinh giỏi gồm 3 học sinh khối 12, 4 học sinh khối 11, 5 học sinh
khối 10.Hỏi có bao nhiêu cách chọn ra 6 học sinh sao cho mỗi khối có ít nhất 1 học sinh
B. Theo chương trình Nâng cao
Câu 7.b (2,0 điểm)
1.Trong mặt phẳng Oxy cho hinh chữ nhật ABCD có diện tích bằng 12,tâm I là giao điểm của
hai đường thẳng d1,d2 lần lượt có phương trình:x-y-3=0 và x+y-6+0.Trung điểm M của cạnh AD
là giao điểm của d1 với trục Ox.Tìm toạ độ các đỉnh của hình chữ nhật
2.Cho elip (E): 2 2
1
16 4
x y
và A(0;2).Tìm B,C thuộc (E) đối xứng với nhau qua Oy sao cho tam
giác ABC đều
Câu8.b (1,0điểm) Tìm m để phương trình: 2 2 2 2
27 1
3
3log (2 2 4 ) log 2 0
x x m m x mx m
có hai nghiệm x1,x2 sao cho x12 + x22 >1
---------------- Hết ----------------
SỞ GD&ĐT BẮC NINH
TRƯỜNG THPT LƯƠNG TÀI 2
ĐỀ THI THỬ ĐẠI HỌC LẦN 2 NĂM HỌC 2012-2013
Môn thi: TOÁN - Khối A,B
Thời gian làm bài 180 phút, không kể thời gian phát đề
==============
Cảmơnbạncónick(auco@ymail.com)gửitớiwww.laisac.page.tl

ĐÁP ÁN TOÁN A,B
CÂU ĐÁP ÁN ĐIỂM
1.(1 điểm)
Khi m=-2,ta có y=x4-2x2+2
*TXĐ
*SBT
-Chiều biến thiên:Tính y’,GPT y’=0
0.25
Nêu khoảng đb,nb
-Cực trị
-Giới hạn
0.25
BBT 0.25
Đồ thị 0.25
2.(1 điểm)
Ta có: y’=4x3+4mx=4x(x2+m)
Đồ thị có 3 điểm cực trị khi và chỉ khi m<0
0.25
Các điểm cực trị A(0;m2+m),
2 2
4 4
( ; ), ( ; )
( ; ), ( ; )
,
B m m C m m
AB m m AC m m
AB m m AC m m
Tam giác ABC cân tại A nên A=1200
4
4
1
os( , )
2
m m
c AB AC
m m
0.25
1
(2điểm)
3
1
3
m ,KL 0.25
3 2
sin 2 3 cos 2 2 os
sin(2 ) sin ( )
52
6
5 2
18 3
PT x x c x
x x
x k
k
x
0.75
2
(1 điểm)
Vì
(0; )
x
nên
5 5 17
, ,
6 18 18
x x x
0.25
Giải hệ phương trình
2 2 2 2
2
( )( 3) 3( ) 2(1)
4 2 16 3 8(2)
x y x xy y x y
x y x
,x y
ĐK:
16
2,
3
x y
3 3
(1) ( 1) ( 1) 2
x y y x
0.25
3
(1 điểm)
Thay y=x-2 vao (2) được
2
4 2 22 3 8
4( 2) 3( 2)
( 2)( 2)
2 2 22 3 4
x x x
x x
x x
x x
2
4 3
( 2) 0(*)
2 2 22 3 4
x
x
x x
0.5
Xét f(x)=VT(*) trên [-2;21/3],có f’(x)>0 nên hàm số đồng biến
suy ra x=-1 là nghiệm duy nhất của (*)
KL: HPT có 2 nghiệm (2;0),(-1;-3)
0.25
4
(1 điểm)
Ta có:
2 2
2 2
2 2 2 2
22
2 2 2
2
2
2
1 3 1 2 5
2 ( 2)( 3) 2 ( 2)( 3)
1 5 1 1
( )
2 3 2 3 2
1 5 3
ln 3 ln
2 2 2
x x
I dx dx
x x x x
dx dx
x x x
x
x C
x
1
Tính được 2
2 , 2 3
1
. 2 3
2
ABCD
BD a AC a
S BD AC a
Tam giác SAB vuông tại S,suy ra SM=a,từ đó tam giác
SAM đều.Gọi H là trung điểm của AM,suy ra
3
( ) ( ) ( )
3
2
SH AB
SAB ABCD SH ABCD
SH a V a
0,25
0,25
Gọi Q là điểm thoả mãn 1
4
AQ AD
MQ//DN
Gọi K là trung điểm của MQ,suy ra HK//AD,HK
MQ,MQ
(SHK)
Góc
giữa SM và DN là góc ^
BAD
0,25
5
(1 điểm)
1 1
3
2 4
os
4
MQ DN
MK
c
SM a a
0,25
6
(1 điểm)
Ta có:
2 2
2 2 2 4 2 4
a b c b a b
c a a a a a a c
b c b c b c
(1)
0,25

Tương tự:
2 2
2 4 (2), 2 4 (3)
b c c a
b b a c c b
c a a b
0,25
Cộng (1),(2),(3) được
2
3( ) 9
a b c a b c
b c a
0,25
3
a b c
b c a
Dấu “=” xảy ra khi a=b=c=1
0,25
1(1 điểm)
Gọi A(x1;y1),B(x2;y2).Vì A,B thuộc đường thẳng x-2y-3=0 nên ta được:
1 1 2 2
2 3 0(1); 2 3 0(2)
x y x y
G là trọng tâm tam giác ABC nên: 1 1 2 2
1 3 ; 1 3
G G
x y x x y y
G thuộc đường thẳng x+y-2=0
1 1 2 2 1 2 1 2
1 1 6 8(3)
x y x y x x y y
AB=5 2 2
1 2 1 2
( ) ( ) 5(4)
x x y y
0,5
Từ (1),(2),(3)
1 2
1 2
22
3
2
3
x x
y y
Từ (1),(2)
1 2 1 2
2( )
x x y y
thay vào (4) được 1 2
1
y y
TH1: 1 2
1
y y
.Tìm được
14 5 8 1
( ; ), ( ; )
3 6 3 6
A B
TH2: 1 2
1
y y
.Tìm được
8 1 14 5
( ; ), ( ; )
3 6 3 6
A B
0,5
2(1 điểm)
(C1) có tâm O(0;0),bán kính 1
13
R
(C2) có tâm I(6;0),bán kính 2
5
R
.
Giao điểm của (C1) và (C2) là (2;3) và (2;-3).Vì A có tung độ dương nên A(2;3)
0,25
Đường thẳng d qua A có pt:a(x-2)+b(y-3)=0 hay ax+by-2a-3b=0
Gọi 1 2
( , ); ( , )
d d O d d d I d
Yêu cầu bài toán trở thành: 2 2 2 2 2 2
2 2 1 1 2 1
12
R d R d d d
2 2 2
2 2 2 2
0
(4 3 ) (2 3 ) 12 3 0
3
b
a b a b b ab
b a
a b a b
0,5
7a
(2 điểm)
*b=0 ,chọ a=1,suy ra pt d là:x-2=0
*b=-3a ,chọ a=1,b=-3,suy ra pt d là:x-3y+7=0
0,25

Tổng số cách chọn 6 học sinh trong 12 học sinh là
6
12
C
0,25
Số học sinh được chọn phải thuộc ít nhất 2 khối
-Số cách chọn chỉ có học sinh khối 12 và khối 11 là:
6
7
C
-Số cách chọn chỉ có học sinh khối 11 và khối 10 là:
6
9
C
-Số cách chọn chỉ có học sinh khối 12 và khối 10 là:
6
8
C
0,5
8a
(1 điểm)
Số cách chọn thoả mãn đề bài là: 6 6 6 6
12 7 9 8
805
C C C C (cách) 0,25
7b
(2 điểm) 1(1 điểm)
Tìm được 9 3
( ; ), (3;0)
2 2
I M
0,25
Lập đươc pt AD:x+y-3=0,Tính được AD=
2 2
0,25
Toạ độ A,D là nghiệm hpt 2 2
3 0
( 3) 2
x y
x y
TÌm được:A(2;1),D(4;-1),C(7;2),B(5;4) hoặc A(2;1),D(4;-1),C(7;2),B(5;4)
0,5
2(1 điểm)
Giả sử B(m;n),C(-m;n).Do B,C thuộc (E) và tam giác ABC đều nên ta được hệ
:
2 2
2 2 2
17 3
13
16 4
17 3
( 2) 4
3
m n m
m n m m
Vậy
17 3 22 17 3 22
( ; ), ( ; )
3 13 3 13
B C
hoặc
17 3 22 17 3 22
( ; ), ( ; )
3 13 3 13
B C
1
BPT đã cho tương đương với
2 2 2 2
3 3
2 2
2 2
2 2
log (2 2 4 ) log ( 2 )
2 0
2 0 1
( 1) 2 2 0 2
x x m m x mx m
x mx m
x mx m x m
x m x m m x m
0,5
8b
(1 điểm)
YCBT
2 2 2
2 2 2
2 2 2
(2 ) (2 ) 2 0 4 0
1 0
(1 ) (1 ) 2 0 2 1 0
2 1
5 2
(2 ) (1 ) 1 5 2 0
m m m m m m
m m m m m m m
m m m m
0,5
Cảmơnbạncónick(auco@ymail.com)gửitớiwww.laisac.page.tl












![Đề thi Tiếng Anh có đáp án [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250810/duykpmg/135x160/64731754886819.jpg)



