1
TRƯỜNG ĐHSP HÀ NỘI
TRƯỜNG THPT CHUYÊN
ĐỀ THI THỬ THPT QUỐC GIA NĂM 2019, LẦN 2
MÔN TOÁN
Ngày thi: 23 - 24/02/2019
Thời gian làm bài: 90 phút.
Mục tiêu: Đề thi thử THPTQG lần 2 của trường THPT Chuyên ĐHSP Hà Nội bám rất sát đề minh họa
của Bộ GD&ĐT. Các câu hỏi với lượng kiến thức lớp 12 và 11. Mức độ câu hỏi không quá khó, trong đề
thi chỉ xuất hiện một vài câu hỏi mang tính chất tương đối khó, và đều là những câu hỏi học sinh đã
được gặp ở được ôn luyện. Đề thi giúp HS ôn luyện tốt nhất và có tâm thể vững vàng nhất để bước vào
kì thi THPTQG sắp tới.
Câu 1: Số nghiệm âm của phương trình
2
log 3 0x
là
A. 2 B. 4 C. 1 D. 3
Câu 2: Tất cả các học sinh của lớp 10A1 đều học giỏi ít nhất một trong hai môn Toán hoặc Tiếng Anh.
Lớp có đúng 30 bạn giỏi Toán, 25 bạn giỏi Tiếng Anh, 16 bạn giỏi cả hai môn Toán và Tiếng Anh. Số
học sinh của lớp 10A1 là
A. 46 B. 39 C. 55 D. 41
Câu 3: Một vật rơi tự do theo phương trình
2
1
2
s gt
, trong đó
2
9,8 /g m s
là gia tốc trọng trường. Giá
trị gần đúng của vận tốc tức thời của chuyển động tại thời điểm
4ts
là
A. 39,2
/ms
B. 9,8
/ms
C. 19,2
/ms
D. 29,4
/ms
Câu 4: Một ôtô đang chạy với vận tốc 9
/ms
thì người lái đạp phanh; từ thời điểm đó, ô tô chuyển
động chậm dần đều với vận tốc
3 9 /v t t m s
, trong đó t là khoảng thời gian tính bằng giây, kể từ
lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu mét?
A. 13,5 m B. 12,5 m C. 11,5 m D. 10,5 m
Câu 5: Cho hàm số
y f x
có đạo hàm trên và có
bảng biến thiên như hình bên. Khẳng định nào sau đây là
đúng?
A. Hàm số đạt cực đại tại điểm
3x
B. Hàm số đạt cực tiểu tại điểm
1x
C. Hàm số đạt giá trị lớn nhất bằng 3
D. Hàm số đạt cực tiểu tại điểm
1
3
x
Câu 6: Trong không gian tọa độ Oxyz, mặt phẳng chứa trục Oz và đi qua điểm
1;2;3I
có phương trình
là
A.
20xy
B.
30z
C.
10x
D.
20y
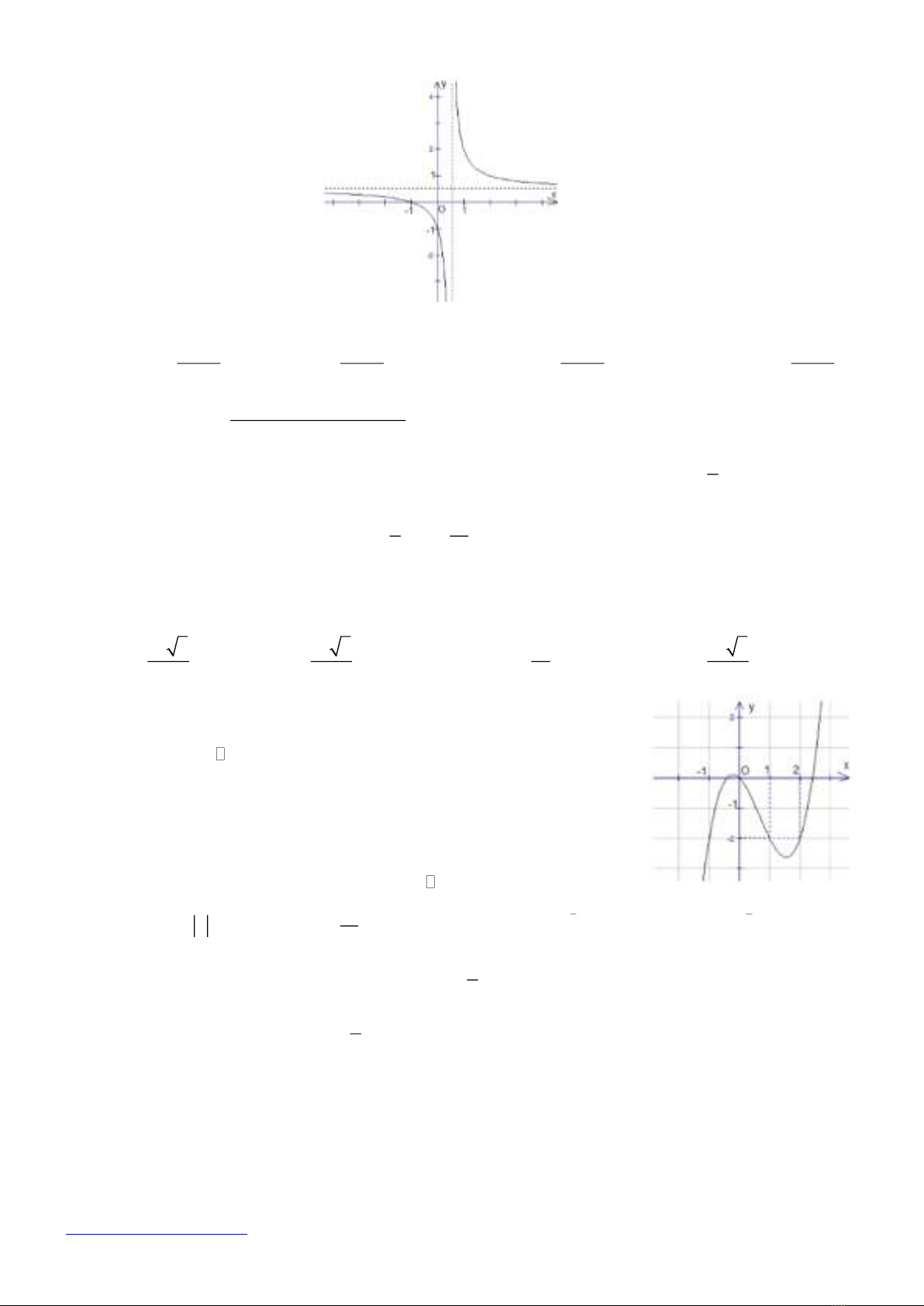
Câu 7: Hàm số nào trong các hàm số sau đây có đồ thị phù hợp với hình bên?
x
1
1
'fx
+
0
0
+
fx
1
3
1
3
1
Mã đề thi 521
2
caodangyhanoi.edu.vn
A.
1
21
x
yx
B.
1
21
x
yx
C.
1
21
x
yx
D.
1
21
x
yx
Câu 8: Giới hạn
2
1 2 3 ... 1
lim
n
nn
n
bằng
A.
B. 1 C. 0 D.
1
2
Câu 9: Tập nghiệm của bất phương trình
2
2 81
3 16
x
là
A.
; 2 2;
B.
;2
C.
2;
D.
2;2
Câu 10: Cho hình chóp đều S.ABCD có tam giác SAC đều cạnh a. Thể tích của khối chóp S.ABCD là
A.
33
4
a
B.
33
12
a
C.
3
6
a
D.
33
3
a
Câu 11: Cho hàm số
y f x
có đồ thị như hình bên và đạo hàm
'fx
liên tục trên . Giá trị của biểu thức
2
1
'f x dx
bằng
A. 2 B. 4
C. 1 D. 0
Câu 12: Hàm số nào sau đây có tập xác định là ?
A.
lnyx
B.
1
x
ye
C.
1
3
yx
D.
1
2x
y
Câu 13: Nếu cấp số nhân
n
u
có công bội q và
15
1,8
2
uu
thì
A.
2q
B.
1
2
q
C.
2q
D.
2; 2q
Câu 14: Trong không gian tọa độ Oxyz, cho hình bình hành ABCD có
1;0;1 , 1;2;1 , 0; 1;2A B C
.
Tọa độ của điểm D là

3
caodangyhanoi.edu.vn
A.
0;3; 1
B.
0; 3;1
C.
2; 3; 2
D.
2;3;0
Câu 15: Cho hàm số
2
3 2 1
11
x khi x
fx mx mx khi x
với m là tham số thực. Tập hợp các giá trị m để hàm
số liên tục tại
1x
là
A.
1
B.
0
C. D.
0;1
Câu 16: Cho hàm số
y f x
liên tục trên R và có đồ thị như hình bên.
Số đường tiệm cận đứng của đồ thị hàm số
1
1
yfx
là
A. 1 B. 2
C. 3 D. 4
Câu 17: Tập hợp các số thực m để phương trình
2
ln 2019 lnx mx x
có nghiệm duy nhất là
A.
B.
1
C.
0
D.
Câu 18: Tập hợp các số thực m để hàm số
3
26 9 1
3
x
y mx m x
có cực trị là
A.
\ 3;3
B. C.
\3
D.
\3
Câu 19: Nền nhà tầng 1 của một hội trường có độ cao 0,8 mét so với mặt đất. Từ nền nhà tầng 1 lên nền
nhà tầng 2 có 1 cầu thang 19 bậc, độ cao của các bậc (so với mặt đất) theo thứ tự lập thành một cấp số
cộng
n
u
có 19 số hạng,
10,95; 0,15ud
(đơn vị là m). Độ cao của bậc thứ 8 so với mặt đất là
A. 1,8m B. 2m C. 2,4m D. 2,2m
Câu 20: Xét các khẳng định sau
i) Nếu
2019a
thì
2019
xx
ax
ii) Nếu
2019a
thì
2019 0
a
b b b
iii) Nếu
2019a
thì
log log 2019 0, 1
bb
a b b
Số khẳng định đúng trong các khẳng định trên là:
A. 3 B. 1 C. 2 D. 0
Câu 21: Nếu các số hữu tỉ
,ab
thỏa mãn
1
0
34
x
ae b dx e
thì giá trị của biểu thức
ab
là
A. 10 B. 8 C. 9 D. 7
Câu 22: Khẳng định nào trong các khẳng định sau là khẳng định đúng?
A. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì không vuông góc với nha
B. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì vuông góc với nhau
C. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau
D. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau
4
caodangyhanoi.edu.vn
Câu 23: Cho
,,a b a b
và hàm số
y f x
thỏa mãn
5
' , 0 0f x x x f
. Khẳng định
nào sau đây là đúng?
A.
66
6
b
a
ba
f x dx
B.
66
6
b
a
f x dx b a
C.
77
42
b
a
ba
f x dx
D.
55
b
a
f x dx b a
Câu 24: Tung 1 con súc sắc cân đối và đồng chất hai lần liên tiếp. Gọi A là biến cố ‘tổng số chấm xuất
hiện ở hai lần tung là một số nhỏ hơn 10’. Xác suất của biến cố A là
A.
1
6
B.
5
6
C.
31
36
D.
32
36
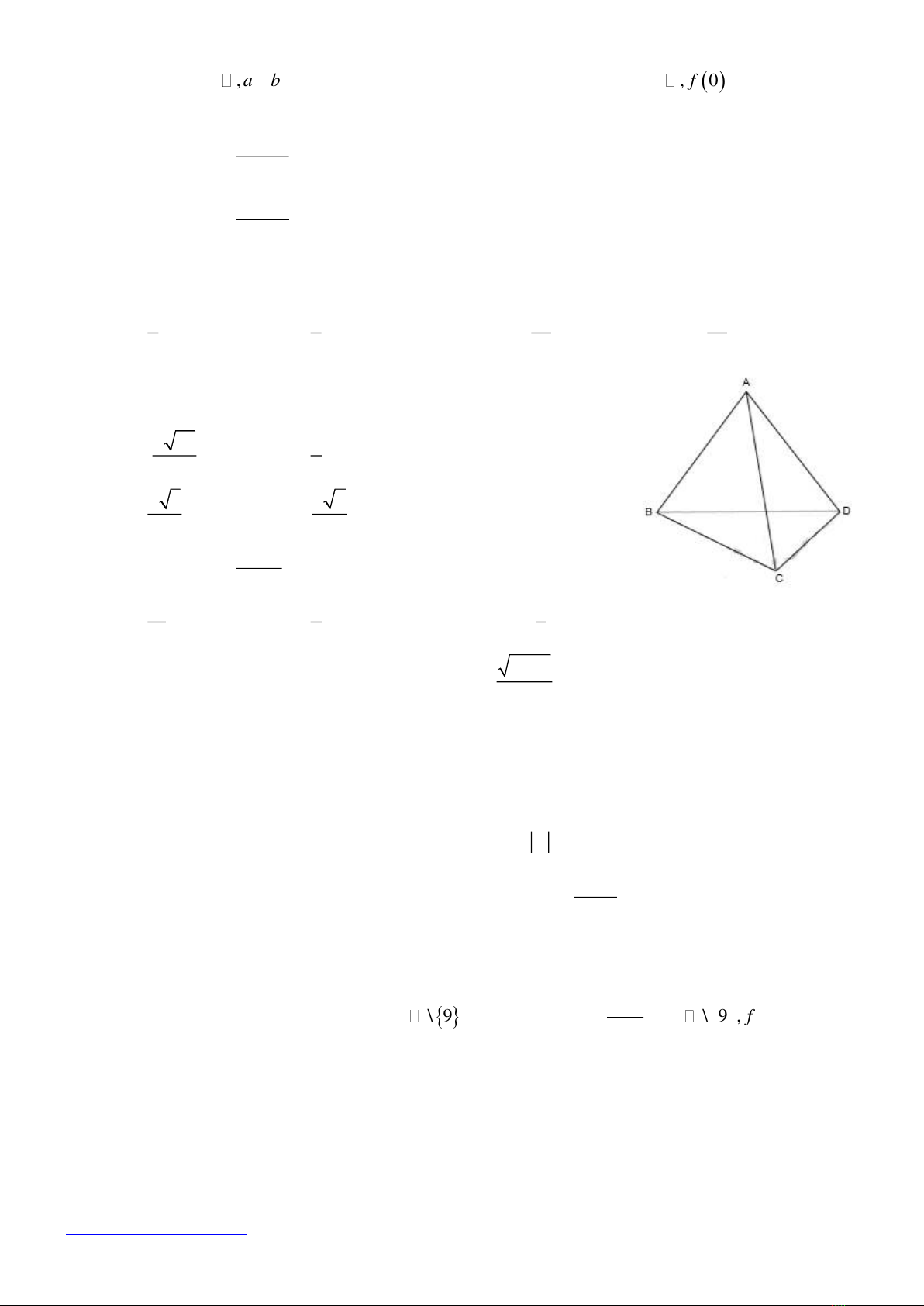
Câu 25: Cho tứ diện ABCD có
00
, 60 , 60 ,AB AC AD a BAC CAD
0
90DAB
. Khoảng cách giữa hai đường thẳng AC và BD là
A.
30
10
a
B.
2
a
C.
3
2
a
D.
2
2
a
Câu 26: Giới hạn
1
45
lim 78
x
x
x
bằng
A.
9
15
B.
4
7
C.
5
8
D. 1
Câu 27: Số đường tiệm cận ngang của đồ thị hàm số
21x
yx
là
A. 2 B. 3 C. 0 D. 1
Câu 28: Cho hình nón có góc ở đỉnh bằng
0
80
. Góc giữa đường thẳng chứa một đường sinh và mặt
phẳng chứa đường tròn đáy bằng
A.
0
80
B.
0
10
C.
0
40
D.
0
50
Câu 29: Số các số nguyên m để hàm số
3sin 4cos 6y x x m x
đồng biến trên tập số thực là
A. 1 B. 4 C. 2 D. 3
Câu 30: Cho tập hợp
0;1; 2;3;4;5;6A
. Số các số có 5 chữ số
abcde
thỏa mãn điều kiện
, , , ,a b c d e
thuộc A và
a b c d e
là
A.
5
7
C
B.
54
76
CC
C.
5
7
A
D.
5!
Câu 31: Cho hàm số
y f x
xác định trên
\9
thỏa mãn
1
' \ 9 , 8 2,
9
f x x f
x
10 2f
. Giá trị của biểu thức
6 . 12ff
là
A. 0 B.
2
ln 3
C.
2
ln 3 4
D.
4
Câu 32: Cho hàm số
x
ya
có đồ thị như hình bên. Giá trị của a là:

5
caodangyhanoi.edu.vn
A. 2 B.
2
log 3
C.
3
D.
3
log 2
Câu 33: Cho hàm số
cos 4yx
có một nguyên hàm
Fx
. Khẳng định nào sau đây là đúng?
A.
01
8
FF
B.
1
0
84
FF
C.
01
8
FF
D.
1
0
84
FF
Câu 34: Một quả bóng đá có dạng hình cầu bán kính 12cm. Diện tích mặt ngoài quả bóng là
A.
2
576
3cm
B.
2
576 cm
C.
2
576 cm
D.
2
144 cm
Câu 35: Giá trị của biểu thức
2019
2019
1
.9
kk
k
AC
bằng
A.
2019
10 2019
B.
2019
10 2020
C.
2019
10 1
D.
2019
10
Câu 36: Cho
,,a b a b
và hàm số
y F x
là một nguyên hàm của hàm số
sinyx
. Khẳng định
nào sau đây là đúng?
A.
' sin sin
b
a
F x dx b a
B.
' sin sin
b
a
F x dx b a
C.
' cos cos
b
a
F x dx b a
D.
' cos cos
b
a
F x dx b a
Câu 37: Trong không gian tọa độ Oxyz, cho mặt cầu
2 2 2
: 2 1 2 9S x y z
và điểm M
thay đổi trên mặt cầu. Giá trị lớn nhất của độ dài đoạn thẳng OM là
A. 12 B. 3 C. 9 D. 6
Câu 38: Cho hàm số
y f x
có đạo hàm là hàm liên tục trên thỏa mãn
2
0
' 45, 0 3f x dx f
.
Giá trị của biểu thức
2f
bằng
A. 42 B. 15 C. 48 D. 135
Câu 39: Một cái phễu gồm một phần có dạng hình trụ, bán kính đáy bằng R và phần còn lại có dạng hình
nón, chiều cao bằng
2R
. Phễu chứa nước có mực nước đến sát đáy hình nón. Người ta thả vào một một
vật hình cầu bằng kim loại vào thì nó đặt vừa khít trong hình nón (hình bên). Chiều cao cột nước dâng lên
theo bằng




















![Đề thi tiếng Anh tốt nghiệp THPT 2025 (Chính thức) kèm đáp án [mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250627/laphong0906/135x160/9121751018473.jpg)





