
Sở GD − ĐT Vĩnh Phúc
Trường THPT Tam Dương
&
ĐỀ THI KHẢO SÁT CHUYÊN ĐỀ LỚP 12
MÔN: TOÁN
Thời gian làm bài 180 phút không kể thời gian phát đề.
Câu 1 (2.0 điểm): Cho hàm số
( ) ( )
= − − + − +
3 2
1 1
1 3 2
3 3
y x m x m x
1. Khào sát sự biến thiên và vẽ đồ thị hàm số khi m = 2.
2. Tìm m để hàm số đạt cực trị tại hai điểm có hoành độ
1 2
,
x x
sao cho
+ =
1 2
2 1
x x
.
Câu 2 (2.0 điểm ) :
1. Giải phương trình: 2
4sin 3 .sin 4cos 3 cos cos 2 1 0
4 4 4
x x x x x
π π π
+ − + − + + =
.
2. Giải bất phương trình: 2 2
2 4
log 2 2 4 log ( 2 2) 5
x x x x
− + + − + ≤
.
Câu 3 (2.0 điểm): Trong không gian với hệ toạ độ Oxyz cho hai điểm A(1; 2; −1),
B(7; −2; 3) và đường thẳng :
1 2 2
:
3 2 2
x y z
+ − −
∆ = =
−
1. Chứng minh rằng đường thẳng AB và đường thẳng ∆ cùng thuộc một mặt phẳng.
2. Tìm điểm I thuộc đường thẳng ∆ sao cho tam giác IAB có chu vi nhỏ nhất.
Câu 4 (2.0 điểm):
1. Tính tích phân: I =
32
0
2( 1) 2 1 1
x
dx
x x x x+ + + + +
∫
.
2. Cho x, y, z ≥ 0. Chứng minh rằng:
( )
2 2 2 2 2 2
3
x xy y y yz z z zx x x y z
+ + + + + + + + ≥ + +
Câu 5 (2.0 điểm):
1. Giải phương trình : 4 3 2
6 9 100 0
z z z
+ + + =
.
2. Trong mặt phẳng Oxy, cho Hypebol (H):
2 2
1
9 4
x y
− =
. Gọi F1, F2 là hai tiêu điểm
của (H). Tìm tọa độ điểm M thuộc (H) sao cho diện tích tam giác MF1F2 bằng
4 13
−−−−−−−−−−−−−HẾT−−−−−−−−−−−−−
Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh:....................................................................SBD:......................
Câu Nội dung Điểm
I
1. Khi m = 2, hàm số có dạng:
= − +
3 2
1 1
3 3
y x x
+ TXĐ: R
+ Sự biến thiên: y’ = x
2
− 2x = 0 ⇔ x = 0 hoặc x = 2
Hàm số đồng biến trên: (−∞; 0) và (2; +∞)
Hàm số nghich biến trên: (0; 2)
Hàm số đạt CĐ tại x
CĐ
= 0, y
CĐ
=
1
3
; đạt CT tại x
CT
= 2, y
CT
= −1
y” = 2x − 2 = 0 ⇔ x = 1
Đồ thị hàm số lồi trên (−∞; 1), lõm trên (1; +∞). Điểm uốn
1
1;
3
−
(1; 2)
0.25
Giới hạn và tiệm cận:
3
3
1 1 1
lim lim 33
x x
y x xx
→±∞ →±∞
= − + = ±∞
0.25
LËp BBT:
0.25
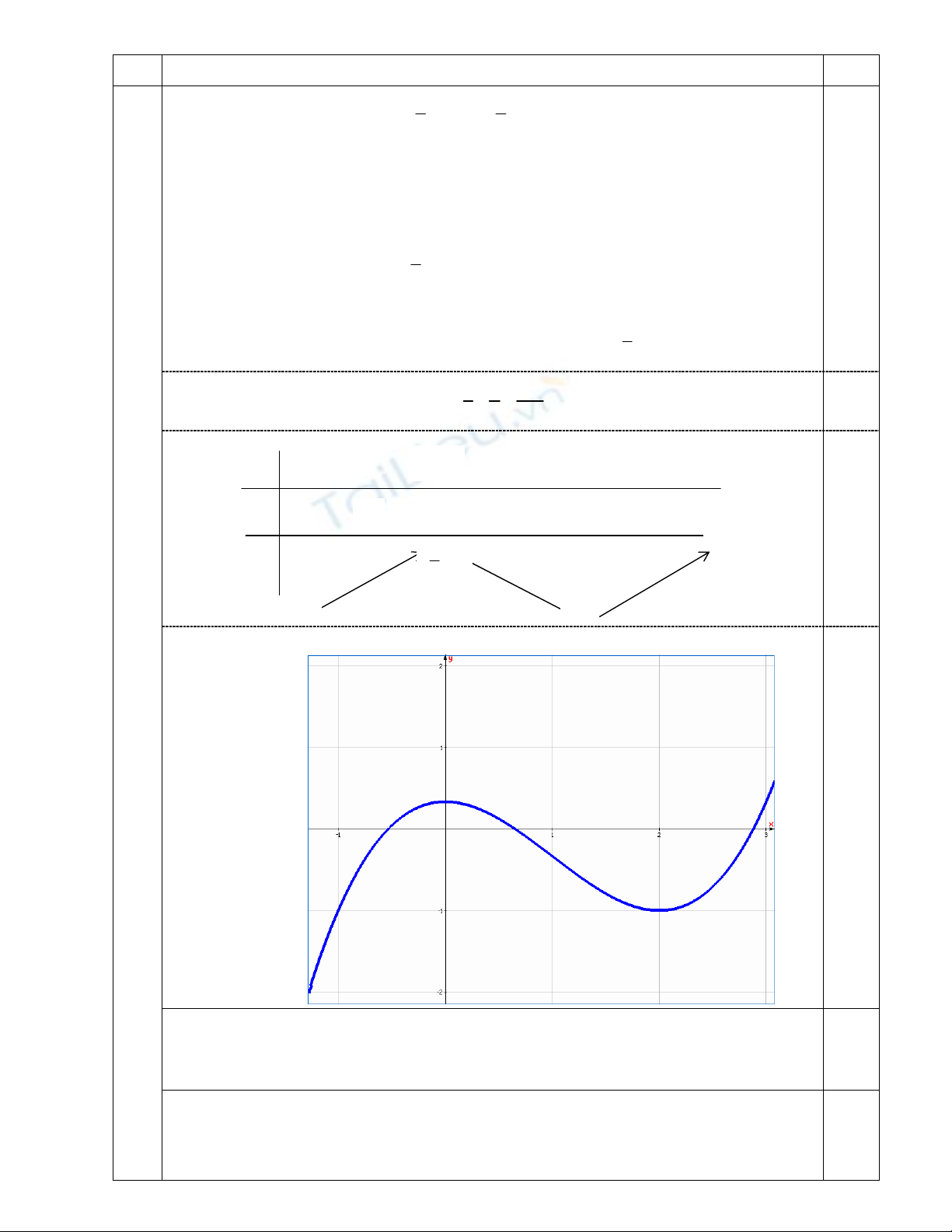
§å thÞ:
0.25
2/. Ta có: y’ = x
2
− 2(m − 1)x + 3(m − 2)
Để hàm số có cực đại và cực tiểu thì y’ = 0 phải có hai nghiệm phân biệt khi và chỉ khi
∆’ > 0 ⇔ m
2
− 5m + 7 > 0 (luôn đúng ∀m)
0.25
Giả sử hoành độ hai điểm cưcj trị là x
1
, x
2
. Khi đó x
1
, x
2
là nghiệm của phương trình y’ = 0.
Theo Viet ta có:
1 2
1 2
2( 1)
3( 2)
x x m
x x m
+ = −
= −
0.25
y’
−
∞
−
1
0
1
3
x
y
+
∞
−
+
+
0
−
∞
2 +
∞
0
x
y
O

Vì x
1
+ 2x
2
= 1
⇒
x
1
= 1 − 2x
2
nên ta có:
( )
2
2 2
3 2
1 2 3( 2)
x m
x x m
= −
− = −
0.25
2
19 3
8 19 9 0
16
m m m ±
⇔ + + = ⇔ =
KL:
0.25
II
2/. Phương trình đã cho tương đương với:
1 sin 4
2(cos 2 sin 2 ) 0
2
x
x x
+
+ + =
(1)
0.25
Đặt
2
cos 2 sin 2 2 cos 2 , | | 2 sin 4 1
4
t x x x t x t
π
= + = − ≤ ⇒= −
0.25
Phương trình tương đương với t(t + 4) = 0 ⇔ t = 0 (Do
| | 2
t≤
) 0.25
Suy ra: 3
cos 2 0 ;
4 8 2
k
x x k
π π π
− = ⇔ = + ∈
0.25
2. Điều kiện: ∀x∈R
Bất phương trình tương đương với:
(
)
2 2
4 4
log 2 2 4 log ( 2 2) 5
x x x x
− + + − + ≤
0.25
Đặt
2
4
log ( 2 2) 0
t x x
= − + ≥
, bất phương trình có dạng: t
2
+ 4t − 5 ≤ 0
⇔ 0 ≤ t ≤ 1 (Vì t ≥ 0)
0.25
Vậy:
2 2 2
4 4
log ( 2 2) 1 log ( 2 2) 1 2 2 0 1 3 1 3
x x x x x x x− + ≤ ⇔ − + ≤ ⇔ − − ≤ ⇔ − ≤ ≤ +
0.25
KL: Tập nghiệm của bất phương trình:
1 3;1 3
T
= − +
0.25
III 1/. Ta có:
(6; 4; 4), (3; 2;
AB u
∆
= − = −
uuur uur
2)
⇒
2
AB u
∆
=
uuur uur
⇒ AB // ∆ ⇒ AB và ∆ cùng thuộc một mặt phẳng.
0.5
Gọi H là trung điểm AB ⇒ H(4 ; 0 ; 1)
Mặt phẳng trung trực AB nhận
AB
uuur
làm vectơ pháp tuyến nên có phương trình:
3
x
− 2
y
+ 2
z
− 14 = 0
0,5
2/. Ta có:
AB
// ∆. Gọi
A
’ là điểm đối xứng của
A
qua đường thẳng ∆.
Ta có chu vi
P
của tam giác
IAB
đạtgiá trị nhỏ nhất khi và chỉ khi
IA
+
IB
đạt giá trị nhỏ
nhất.
Từ cách dựng ta có:
IA
+
IB
=
I
’
A
+
IB
≥
A
’
B
.
Đẳng thức xảy ra khi và chỉ khi
I
trùng
với
H
0
.
0.25
Do
AB
// ∆ nên tam giác
AA
’
B
vuông tại
A
và
AH
0
là đường trung tuyến.
⇒ ∆
H
0
AB
cân tại
H
0
⇒
HH
0
⊥ ∆ ⇒
H
0
(2 ; 0 ; 4) 0.25
Vậy
I
trùng
H
0
(2; 0; 4) thì ∆
AIB
có chu vi nhỏ nhất và min
P
=
(
)
2 17 30
+
0.25
H
A'
AB
H
0
I

0.25
IV
1/. Đặt
2
1 1 2
t x t x dx tdt
= + ⇒= + ⇒=
Với
x
= 0 ⇒
t
= 1;
x
= 3 ⇒
t
=2
0.25
2 2
2 2 2
2
1 1
2 ( 1)
2 ( 1)
( 1)
t t dt
I t dt
t t
−
= = −
+
∫ ∫
0.5
2
3
1
2 2
( 1)
3 3
t
= − =
0.25
2/. Ta có:
2 2 2 2 2 2
1
3( 2 ) ( 2 )
4
x xy y x xy y x xy y
+ + = + + + − +
2 2 2 2 2
1 3 3
3( ) ( ) ( ) ( )
4 4 2
x y x y x y x xy y x y
= + + − ≥ + ⇒+ + ≥ +
0.5
Tương tự:
2 2 2 2
3 3
( ); ( )
2 2
y yz z y z z zx x z x
+ + ≥ + + + ≥ +
0.25
⇒ Cộng vế với vế ta có điều phải chứng minh. 0.25
V
1/. Phương trình tương đương với: (z + 3z)
2
− (10i)
2
= 0
⇔ (z
2
+ 3z − 10i)(z
2
+ 3z + 10i) = 0
2
2
3 10 0
3 10 0
z z i
z z i
+ − =
⇔
+ + =
0.5
Với z
2
+ 3z − 10i = 0 có ∆ = (5 + 4i)
2
⇒ phương trình có nghiệm
1 2
4 2
z i
z i
= +
⇔
= − −
0.25
Với z
2
+ 3z + 10i = 0 có ∆ = (5 − 4i)
2
⇒ phương trình có nghiệm
1 2
4 2
z i
z i
= −
⇔
= − +
0.25
2. Hypebol có hai tiêu điểm
(
)
(
)
1 2
13;0 , 13;0
F F
−
G
ọ
i
h
là chi
ề
u cao h
ạ
t
ừ
M
c
ủ
a ∆
MF
1
F
2
. Vì di
ệ
n tích ∆
MF
1
F
2
=
4 3
nên
h
= 4
0.25
Vì
F
1
,
F
2
∈
Ox
nên
y
M
= 10. Gi
ả
s
ử
M
(
a
; 4) thu
ộ
c (H). (
a
> 0) 0.25
Hoành
độ
M
là nghi
ệ
m c
ủ
a ph
ươ
ng trình:
2 2 2
4
1 45 3 5
9 4
aa a− = ⇔ = ⇔ = ±
T
ươ
ng t
ự
v
ớ
i
a
< 0
0.25
KL: Có 4
đ
i
ể
m
M
c
ầ
n tìm:
(
)
(
)
(
)
(
)
1 2 3 4
3 5; 4 , 3 5; 4 , 3 5; 4 , 3 5; 4
M M M M
− − − −
0.25


























