
CHUYÊN Đ: C C TR HÌNH H CỀ Ự Ị Ọ
C C TR HÌNH H CỰ Ị Ọ
A- Phương pháp giải bài toán cực trị hình học.
1- D ng chung c a bài toán c c tr hình h c :ạ ủ ự ị ọ
“ Trong t t c các hình có chung m t tính ch t , tìm nh ng hình mà m t điấ ả ộ ấ ữ ộ ạ
l ng nào đó ( đ dài đo n th ng , s đo góc, s đo di n tích …) có giá tr l nượ ộ ạ ẳ ố ố ệ ị ớ
nh t ho c giá tr nh nh t.”ấ ặ ị ỏ ấ và có th đc cho d i các d ng :ể ượ ướ ạ
a) Bài toán v d ng hình .ề ự
Ví d : Cho đng tròn (O) và đi m P n m trong đng tròn , xác đnh v trí c aụ ườ ể ằ ườ ị ị ủ
dây đi qua đi m P sao cho dây đó có đ dài nh nh t.ể ộ ỏ ấ
b) Bài toán v ch ng minh .ể ứ
Ví d : Ch ng minh r ng trong các dây đi qua đi m P trong m t đng tròn (O),ụ ứ ằ ể ộ ườ
dây vuông góc v i OP có đ dài nh nh t.ớ ộ ỏ ấ
c) Bài toán v tính toán.ề
Ví d : Cho đng tròn (O;R) và đi m P n m trong đng tròn có OP = h , Tínhụ ườ ể ằ ườ
đ dài nh nh t c a dây đi qua P.ộ ỏ ấ ủ
2- H ng gi i bài toán c c tr hình h c :ướ ả ự ị ọ
a) Khi tìm v trí c a hình H trên mi n D sao cho bi u th c f có giá tr l n nh t taị ủ ề ể ứ ị ớ ấ
ph i ch ng t đc :ả ứ ỏ ượ
+V i m i v trí c a hình H trên mi n D thì f ớ ọ ị ủ ề ≤ m ( m là h ng s )ằ ố
+Xác đnh v trí c a hình H trên mi n D sao cho f = mị ị ủ ề
b) Khi tìm v trí c a hình H trên mi n D sao cho bi u th c f có giá tr nh nh t taị ủ ề ể ứ ị ỏ ấ
ph i ch ng t đc :ả ứ ỏ ượ
+V i m i v trí c a hình H trên mi n D thì f ớ ọ ị ủ ề ≥ m ( m là h ng s )ằ ố
+Xác đnh v trí c a hình H trên mi n D đ f = m ị ị ủ ề ể
3 - Cách trình bày l i gi i bài toán c c tr hình h c .ờ ả ự ị ọ
+ Cách1 :Trong các hình có tính ch t c a đ bài,ch ra m t hình r i ch ngấ ủ ề ỉ ộ ồ ứ
minh m i hình khác đu có giá tr c a đi l ng ph i tìm c c tr nh h n ( ho cọ ề ị ủ ạ ượ ả ự ị ỏ ơ ặ
l n h n ) giá tr c a đi l ng đó c a hình đã ch ra.ớ ơ ị ủ ạ ượ ủ ỉ
1
A
BHC
h.4
a
CHUYÊN Đ: C C TR HÌNH H CỀ Ự Ị Ọ
+ Cách2 :Bi n đi t ng đng đi u ki n đ đi l ng này đt c c tr b iế ổ ươ ươ ề ệ ể ạ ượ ạ ự ị ở
đi l ng khác đt c c tr cho đn khi tr l i đc câu h i mà đ bài yêu c u.ạ ượ ạ ự ị ế ả ờ ượ ỏ ề ầ
Ví d : Cho đng tròn (O) và đi m P n m trong đng tròn( P không trùng v iụ ườ ể ằ ườ ớ
O).Xác đnh v trí c a dây đi qua đi m P sao cho dây đó có đ dài nh nh t.ị ị ủ ể ộ ỏ ấ
Gi i :ả
+Cách 1 :
G i AB là dây vuông góc v i OP t i P , và dây CD là dây b t k đi qua P vàọ ớ ạ ấ ỳ
không trùng v i AB ( h.1). ớ
K OH ẻ CD .
OHP vuông t i H ạ OH < OP CD > AB
Nh v y trong t t c các dây đi qua P , dây vuông gócư ậ ấ ả
v i OP t i P có đ dài nh nh t .ớ ạ ộ ỏ ấ
+Cách 2 :
Xét dây AB b t k đi qua P ( h.2). K OH ấ ỳ ẻ AB
Theo liên h gi a dây và kho ng cách đn tâm:ệ ữ ả ế
AB nh nh t ỏ ấ OH l n nh tớ ấ
Ta l i có OH ≤ OP ạ
OH = OP H P≡
Do đó maxOH = OP
Khi đó dây AB vuông góc v i OP t i P.ớ ạ
B-Các kiến thức thường dùng giải bài toán cực trị hình học.
1- S d ng quan h gi a đng vuông góc , đng xiên , hình chi u .ử ụ ệ ữ ườ ườ ế
a-Ki n th c c n nh :ế ứ ầ ớ
a1) ABC vuông t i A (có th suy bi n thành đo n th ng) ạ ể ế ạ ẳ AB ≤ BC .
D u “=” x y ra ấ ả A ≡C . ( h.3 )
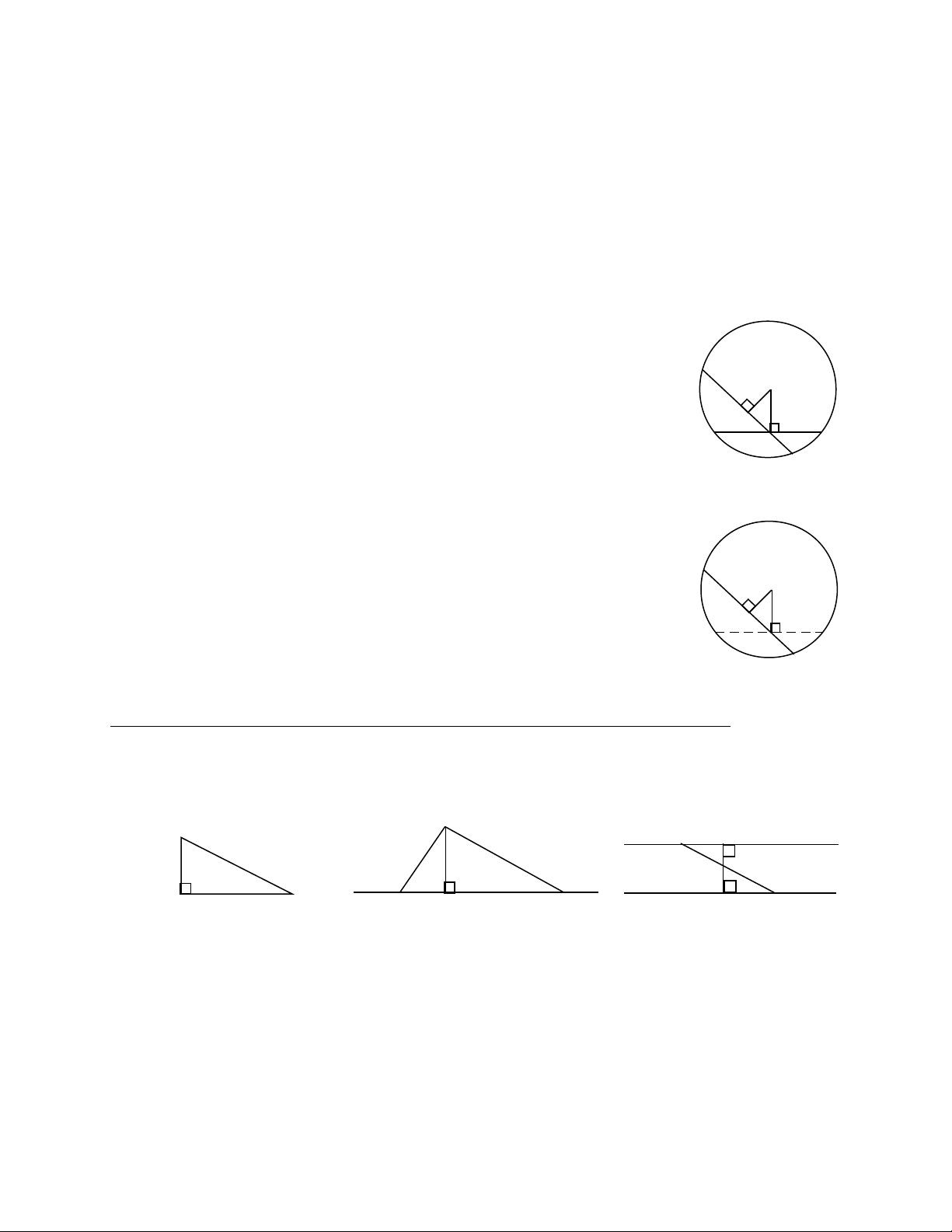
a2) ( h.4 )
+ AH a AH ≤ AB . D u “=” x y ra ấ ả B ≡H .
+ AB < AC HB < HC
2
H
O
C
D
AB
P
h .1
H
O
A
B
P
h .2
A
B
C
h.3
A
B
H
K a
b
h.5
CHUYÊN Đ: C C TR HÌNH H CỀ Ự Ị Ọ
a3)( h.5 )
A,K a; B, H b; a // b ; HK a HK ≤ AB
D u “=” x y ra ấ ả A ≡K và B ≡ H .
b-Các ví d :ụ
Ví d 1: ụTrong các hình bình hành có hai đng chéo b ng 6 cm và 8 cm ,hìnhườ ằ
nào có di n tích l n nh t ? Tính di n tích l n nh t đó.ệ ớ ấ ệ ớ ấ
Gi i :ả
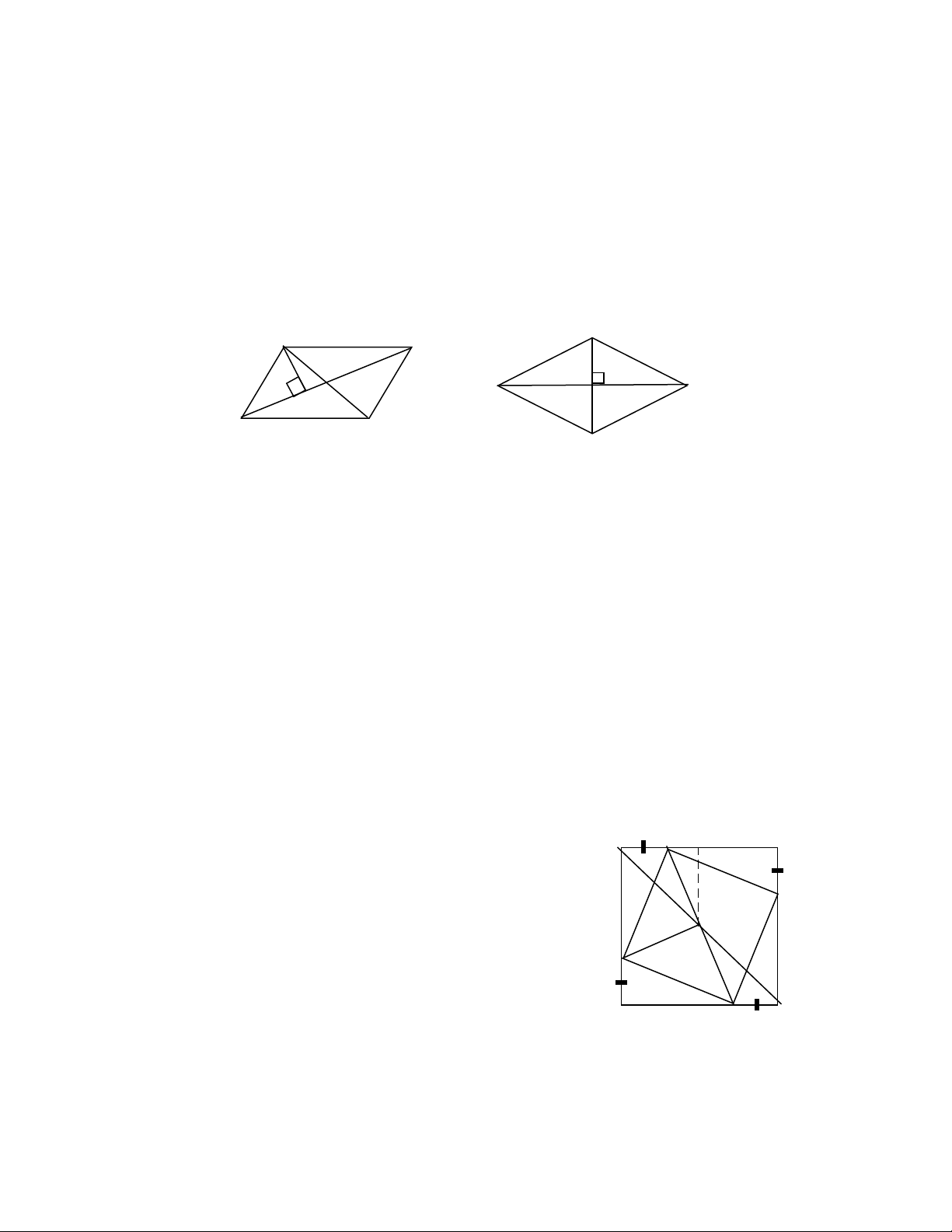
Xét hình bình hành ABCD có AC = 8 cm; BD = 6 cm ( h.6)
G i O là giao đi m hai đng chéo . K BH ọ ể ườ ẻ AC .
Ta có : SABCD = 2SABC = AC.BH
Ta có AC = 8cm, BH ≤ BO = 3cm. Do đó :
SABCD ≤ 8.3 = 24 (cm2)
SABCD = 24 cm2 BH ≡ BO H ≡ O BD AC
V y max SậABCD = 24 cm2 . Khi đó hình bình hành ABCD là hình thoi (h.7) có
di n tích 24cmệ2.
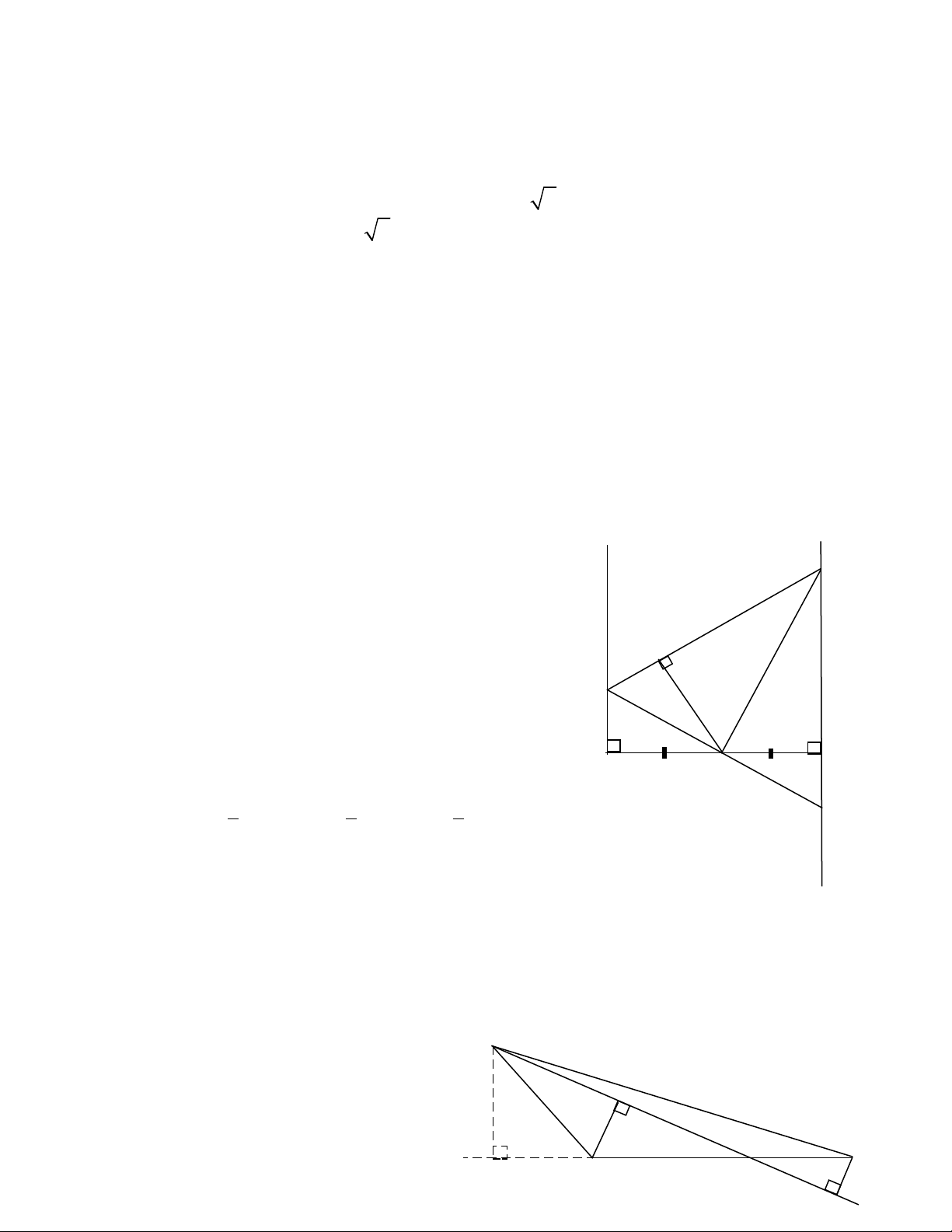
Ví d 2:ụ Cho hình vuông ABCD . Trên các c nh AB,BC ,CD,DA ta l y theo thạ ấ ứ
t các đi m E,F,G,H sao cho AE = BF = CG = DH . Xác đnh v trí c a các đi m E,ự ể ị ị ủ ể
F,G,H sao cho t giác EFGH có chu vi nh nh t .ứ ỏ ấ
Gi i :ả
HAE = EBF = FCG = GHD
HE = EF = FG = GH
EFGH là hình thoi .
ᄋ
ᄋ
AHE BEF=
ᄋ ᄋ
0
AHE AEH 90+ =
ᄋ
ᄋ
0
BEF AEH 90+ =
ᄋ
0
HEF 90=
EFGH là hình vuông
3
A
C
D
B
O
HA
B
C
D
O H≡
h.6 h.7
A
D
B
C
E K
F
G
H
HO
h.8
CHUYÊN Đ: C C TR HÌNH H CỀ Ự Ị Ọ
G i O là giao đi m c a AC và EG . T giác AECG có AE = CG, AE //CG nên làọ ể ủ ứ
hình bình hành suy ra O là trung đi m c a AC và EG , do đó O là tâm c a c haiể ủ ủ ả
hình vuông ABCD và EFGH.
HOE vuông cân : HE2 = 2OE2 HE = OE
2
Chu vi EFGH = 4HE = 4
2
OE . Do đó chu vi EFGH nh nh t ỏ ấ OE nh nh t ỏ ấ
K OK ẻAB OE ≥OK ( OK không đi )ổ
OE = OK E ≡ K
Do đó minOE = OK
Nh v y , chu vi t giác EFGH nh nh t khi và ch khi E,F,G,H là trung đi mư ậ ứ ỏ ấ ỉ ể
c a AB , BC, CD, DA.ủ
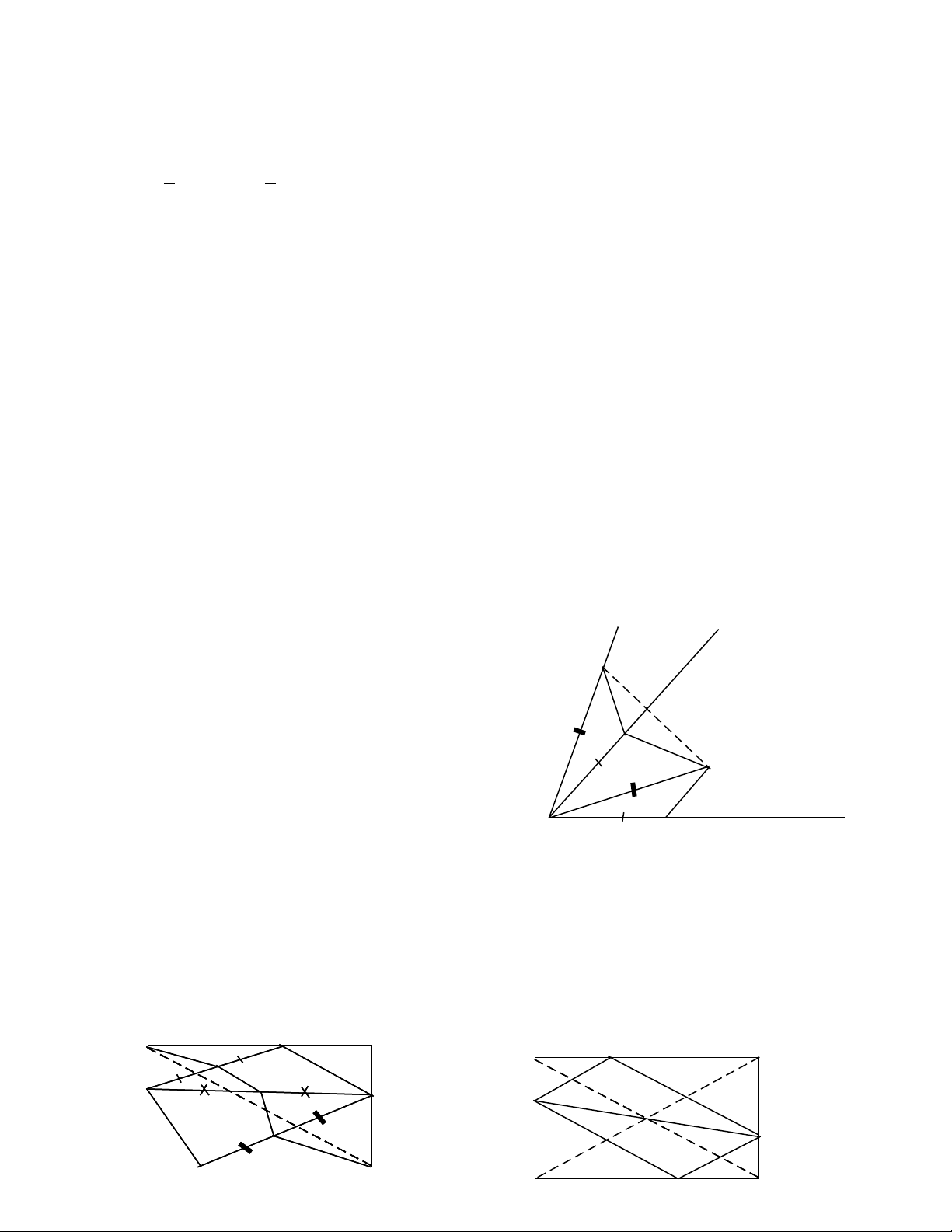
Ví d 3: ụCho đo n th ng AB có đ dài 2a .V v m t phía c a AB các tia Axạ ẳ ộ ẽ ề ộ ủ
và By vuông góc v i AB . Qua trung đi m c a M c a AB có hai đng th ng thayớ ể ủ ủ ườ ẳ
đi luôn vuông góc v i nhau và c t Ax, By theo th t t i C và D .xác đnh v trí c aổ ớ ắ ứ ự ạ ị ị ủ
các đi m C,D sao cho tam giác MCD có di n tích nh nh t .Tính di n tích tam giácể ệ ỏ ấ ệ
đó.
Gi i:ả
G i K là giao đi m c a CM và DB ọ ể ủ
MA = MB ;
ᄋ
ᄋ
0
A B 90= =
,
ᄋ
ᄋ
AMC BMK=
MAC = MBK MC = MK
M t khác DM ặCK
DCK cân
ᄋ ᄋ
1 2
D D=
K MH ẻ CD .
MHD = MBD MH = MB = a
SMCD =
1
2
CD.MH ≥
1
2
AB.MH =
1
2
2a.a= a2
SMCD = a2 CD Ax khi đó
ᄋ
AMC
= 450 ;
ᄋ
BMD
=450.
V y min SậMCD = a2 . Các đi m C,D đc xác đnh trên Ax; By sao cho AC = BC =a .ể ượ ị
Ví d 4: ụCho tam giác ABC có
ᄋ
B
là góc tù , đi m D di chuy n trên c nh BC .ể ể ạ
Xác đnh v trí c a đi m D sao cho t ng các kho ng cách t B và C đn đngị ị ủ ể ổ ả ừ ế ườ
th ng AD có giá tr l n nh t .ẳ ị ớ ấ
Gi i:ả
G i S là di n tích ọ ệ ABC Khi D di
chuy n trên c nh BC ta có :ể ạ
4
C
AB
K
H
D
M
12
yx
h.9
C
A
B D
F
E
h.10
H
CHUYÊN Đ: C C TR HÌNH H CỀ Ự Ị Ọ
SABD + SACD = S
K BE ẻAD , CF AD
1
2
AD.BE +
1
2
AD.CF = S
BE +CF =
2S
AD
Do đó BE + CF l n nh t ớ ấ AD nh nh t ỏ ấ hình chi u HD nh nh t ế ỏ ấ
Do HD ≥ HB ( do
ᄋ
ABD
>900 ) và HD = HB D B ≡
V y Khi D B thì t ng các kho ng cách t B và C đn AD có giá tr l n nh t .≡ậ ổ ả ừ ế ị ớ ấ
2- S d ng quan h gi a đng th ng và đng g p khúc.ử ụ ệ ữ ườ ẳ ườ ấ
a-Ki n th c c n nh :ế ứ ầ ớ
V i ba đi m A,B,C b t k ta có : AC +CB ≥ ABớ ể ấ ỳ
AC +CB = AB C thu c đo n th ng ABộ ạ ẳ
b-Các ví d :ụ
Ví d 5:ụCho góc
ᄋ
xOy
và đi m A n m trong góc đó . Xác đnh đi m B thu c tiaể ằ ị ể ộ
Ox, đi m C thu c tia Oy sao cho OB = OC và t ng AB +AC là nh nh t .ể ộ ổ ỏ ấ
Gi i:ả
K tia Om n m ngoài góc xOy sao choẻ ằ
ᄋ
ᄋ
yOm xOA=
. Trên tia Om l y đi m D saoấ ể
cho OD = OA . Các đi m D và A c đnh .ể ố ị
OD =OA, OC = OB ,
ᄋ
ᄋ
COD BOA=
DOC = AOB CD = AB
Do đó AC +AB = AC +CD
Mà AC +CD ≥ AD
AC +AB ≥ AD
X y ra đng th c khi và ch khi C ả ẳ ứ ỉ AD
V y min(AC+AB) =AD . Khi đó C là giao đi m c a AD và Oy , B thu c tia Oxậ ể ủ ộ
sao cho OB = OC.
Ví d 6:ụCho hình ch nh t ABCD và đi m E thu c c nh AD . Xác đnh v tríữ ậ ể ộ ạ ị ị
các đi m F thu c c nh AB , G thu c c nh BC , H thu c c nh CD sao cho t giácể ộ ạ ộ ạ ộ ạ ứ
EFGH có chu vi nh nh t.ỏ ấ
Gi i :ả
5
h.11
Ox
A
B
C
D
my
A
E
D
FB
C
G
H
I
K
M
h.12
A
E
D
FB
C
G
H
I
K
M
h.12
A
E
D
FB
C
G
H
I
K
M
h.13


























