1Bài giảng 4
408001
Biến ñổi năng lượng ñiện cơ
TS. Nguyễn Quang Nam
HK2, 2009 – 2010
http://www4.hcmut.edu.vn/~nqnam/lecture.php
nqnam@hcmut.edu.vn
2Bài giảng 4
Các mô hình ñộng học của hệthống ñiện ñược mô tảbởi các phương trình vi
phân. Tính ổn ñịnh của hệthống phi tuyến trong vận hành ñược ñặc biệt quan
tâm. Một sốcông cụphân tích tính ổn ñịnh sẽ ñược giới thiệu.
Nghiệm trong miền thời gian của bài toán ñộng học hệthống có ñược bằng
việc tính tích phân sốvà các ñiểm cân bằng ñược xác ñịnh bằng ñồ thị. Với các
hệthống bậc cao hơn, các kỹthuật số ñược sửdụng ñể tính các ñiểm cân bằng.
Sẽcó ích nếu biết ñiểm cân bằng tĩnh là ổn ñịnh hay không. Với các nhiễu
mạnh của trạng thái xhay ngõ vào u, luôn cần các mô phỏng trong miền thời
gian. Với các thay ñổi nhỏ quanh ñiểm cân bằng, một phân tích tuyến tính hóa là
ñủ ñể xác ñịnh ñiểm cân bằng là ổn ñịnh hay không. ðôi khi, các hàm năng lượng
có thể ñược dùng ñể ñánh giá tính ổn ñịnh của hệthống ñối với nhiễu mạnh mà
không cần các mô phỏng trong miền thời gian.
Ổn ñịnh các hệthống ñiện cơ – Giới thiệu
3Bài giảng 4
ðiểm cân bằng sẽbiểu diễn trạng thái vận hành xác lập của hệthống, chẳng
hạn một lưới ñiện. Hệvật lý có thểchịu thay ñổi nhỏ(ví dụ thay ñổi tải), vốn có
thểdẫn ñến dao ñộng hay thậm chí sụp ñổ hệthống, hoặc các nhiễu mạnh (ví dụ,
sựcốhay sét ñánh).
Với trường hợp vô hướng, mô hình hệthống là
Tuyến tính hóa
(
)
uxfx ,
=
&
Khai triển f(x, u) thành 1 chuỗi Taylor quanh ñiểm cân bằng xevà ngõ vào
không ñổi, và chỉgiữlại các sốhạng bậc nhất
u
ˆ
( )
( ) ( )
( )
( )
u
u
f
x
x
f
uxfuu
u
f
xx
x
f
uxfuxf eee ∆
∂
∂
+∆
∂
∂
+=−
∂
∂
+−
∂
∂
+=
0000
ˆ
,
ˆˆ
,,
Hay
( )
( )
u
u
f
x
x
f
uxfuxfx
e
∆
∂
∂
+∆
∂
∂
=−=∆
00
ˆ
,,
&
4Bài giảng 4
Gọi , , và . Tuyến tính hóa hệ quanh
ñiểm cân bằng dẫn ñến
Tuyến tính hóa hệbậc hai
(
)
uxxfx ,,
2111
=
&
(
)
uxxfx ,,
2122
=
&
e
xxx
111
−=∆
e
xxx
222
−=∆
uuu
ˆ
∆
u
u
f
u
f
x
x
x
f
x
f
x
f
x
f
x
x∆
∂
∂
∂
∂
+
∆
∆
∂
∂
∂
∂
∂
∂
∂
∂
=
∆
∆
0
2
0
1
2
1
0
2
2
0
1
2
0
2
1
0
1
1
2
1
&
&
A
Trịriêng của Acó ñược bằng cách giải det(A – λI) = 0. Hệthống là ổn ñịnh nếu
tất cảcác trịriêng nằm ởnửa trái của mặt phẳng phức (nghĩa là, phần thực < 0).
5Bài giảng 4
Ổn ñịnh của hệbậc hai
(
)
xx
x
xf
M
x
dt
d
M
B
dt
xd ∆−=∆
∂
∂
=∆+
∆
2
0
0
2
2
1
ω
Xét mô hình một hệbậc hai
( )
uxf
dt
dx
B
dt
xd
M,
2
2
=+
có dạng tuyến tính hóa
ðịnh nghĩa và , dạng không gian trạng thái trởthành
1
xx ∆=∆ 2
xx ∆=∆&
∆
∆
−−
=
∆
∆
2
1
2
0
2
1
10
x
x
MB
x
x
ω
&
&
Phương trình ñặc tính có ñược
0
1
2
0
=
−−−
−
λω
λ
MB 0
2
0
2
=++
ωλλ
M
B
6Bài giảng 4
Ổn ñịnh của hệbậc hai (tt)
Trường hợp I (B > 0, M > 0, )
0
2
0
>
ω
2
0
2
2
4
ω
>
M
B
2
0
2
2
4
ω
=
M
B
2
0
2
2
4
ω
<
M
B
Trong cả 3 trường hợp, hệlà ổn ñịnh.
Trường hợp II (B > 0, M > 0, )
Trường hợp ñặc biệt (B = 0, M > 0): hệlà không ổn ñịnh nếu , hay ở
biên ổn ñịnh nếu .
Vd. 5.1 sẽ ñược trình bày tại lớp.
0
2
0<
ω
Nghiệm tổng quát của phương trình ñặc tính
2
0
2
2
21
4
2
,
ωλλ
−±−= M
B
M
B
0
2
0
>
ω
0
2
0
<
ω
7Bài giảng 4
Phương pháp hàm năng lượng cho hệphi tuyến
Với nhiễu mạnh, việc phân tích ổn ñịnh của hệphi tuyến có thểcần ñến các kỹ
thuật tính sốvốn rất tốn kém sức mạnh tính toán. Trong nhiều trường hợp, thông
tin hữu ích có thể thu ñược bằng một phương pháp trực tiếp, tránh việc phải tính
tích phân số. Kỹthuật này giữa trên các hàm năng lượng, và ñược gọi là là
phương pháp Lyapunov. Có thể thu ñược các lời giải tốt với các hệbảo toàn.
Trong các hệbảo toàn, tổng năng lượng là không ñổi, và ñiều này ñược dùng
trong phân tích ổn ñịnh các hệnày. Xét con lắc trong hình 5.2, bao gồm khối
lượng Mnối vào một ñiểm tựa không ma sát bằng một thanh cứng.
Coi V(θ) = 0 tại θ= 0, khi ñó tại vịtrí bất kỳθ, thế năng ñược cho bởi
(
)
(
)
(
)
θ
θ
cos1
−
=
MglV
8Bài giảng 4
Hệbảo toàn
Không có lực nào khác ngoài trọng lực, và hệlà bảo toàn, vậy
( )( )
θ
θ
sin
2
2
lMg
dt
d
J−=
Vếphải có thể ñược biểu diễn như một ñạo hàm âm của một hàm thế vô
hướng. Trong trường hợp này,
( ) ( )( )
[ ]
(
)
θ
θ
θ
θ
θ
∂
∂
−=−
∂
∂
−=− V
MglMgl cos1sin
(
)
θ
θθ
∂
∂
−= V
dt
d
J
2
2
Dẫn ñến
Các ñiểm cân bằng là nghiệm của
(
)
( )
0sin =−=
∂
∂
−
θ
θ
θ
Mgl
V
Trong khoảng –π ñến +π,0 ,
πθ
±=
e
9Bài giảng 4
Năng lượng
Xét
(
)
0
2
2
=
∂
∂
+
θ
θθ
V
dt
d
J
Nhân với dθ/dt ñể có
( )
{
EV
dt
d
J=+
energy Potential
energy Kinetic
2
2
1
θ
θ
43421
(
)
0
2
2
=
∂
∂
+dt
dV
dt
d
dt
d
J
θ
θ
θθθ
Tích phân theo t ñể thu ñược
Việc phân tích ổn ñịnh có thể ñược thực hiện cho 3 trường hợp (xem sách),
bằng khái niệm giếng thế năng.
10Bài giảng 4
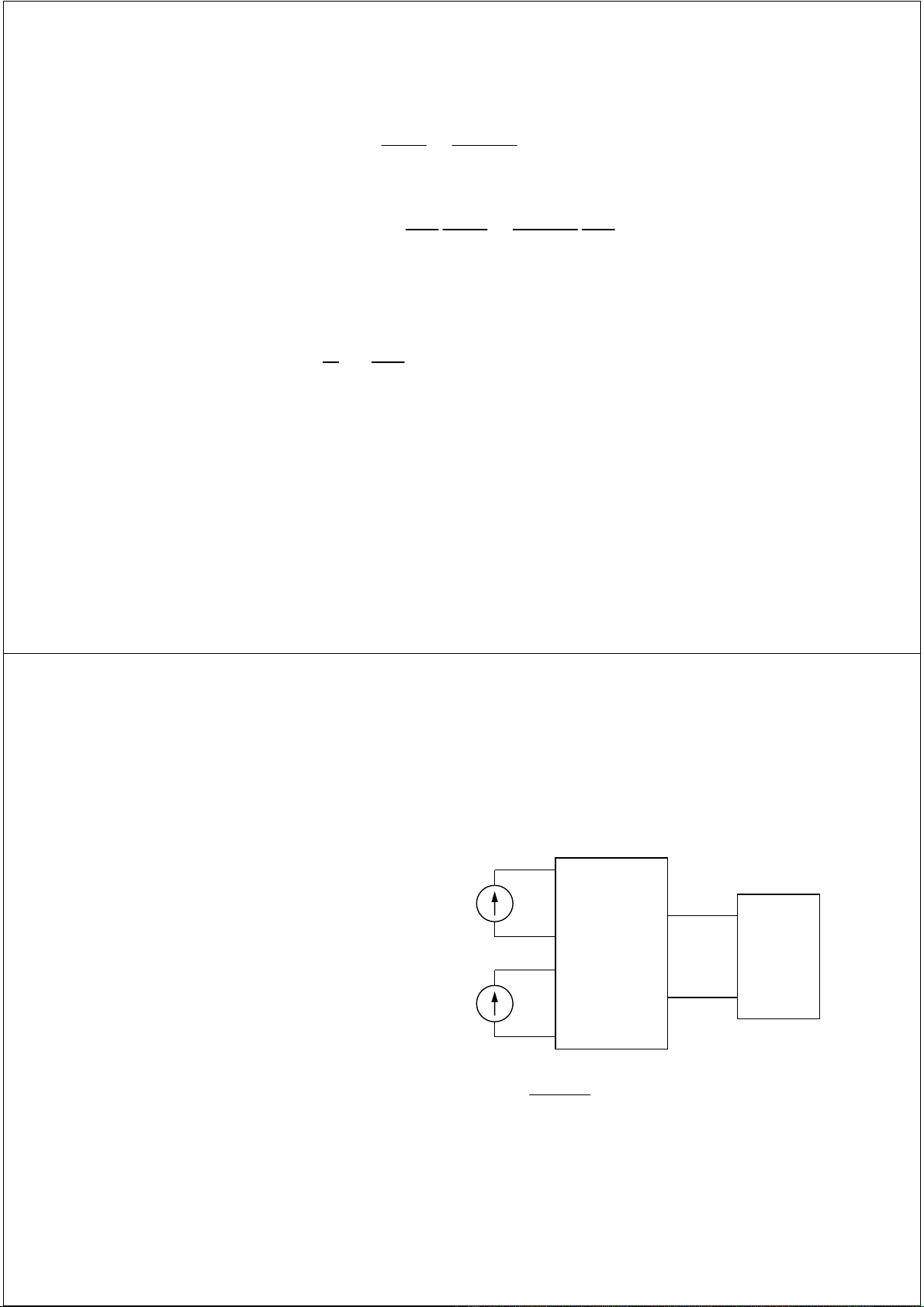
Hàm năng lượng trong hệ ñiện cơ
Xét hệ bên dưới, giảthiết cảhệ ñiện lẫn hệ cơ ñều không chứa các phần tử
tiêu tán năng lượng.
Mech.
system
Ghép
ñiện
cơ
Teor fe
θor x
+
_
+
_
+
_
I2
I1
λ1
λ2
Nếu λhoặc i ởmỗi cửa ñược giữ
không ñổi, có thểdự ñoán một dịch
chuyển ñều trong hệ cơ. Không có
dòng chảy năng lượng hay ñồng năng
lượng vào cửa ñiện. Ởhệ cơ, giảthiết
không có phần tửtiêu tán năng lượng.
Thế năng tổng quát hóa:
(
)
(
)
(
)
θθθ
,,
21
'
IIWUV
m
−=
(
)
(
)
(
)
θ
θ
θ
,,
21
Λ
Λ
+
=
m
WUV
(dòng hằng i1và i2)
(từthông móc vòng hằng λ1và λ2)
(
)
θ
θ
∂
∂
−= U
T
m
(lực cơ tác ñộng)