Bài giảng Cơ học lý thuyết: Chương 6 - Huỳnh Vinh

Chia sẻ: Bánh Bèo Xinh Gái | Ngày: | Loại File: PDF | Số trang:28

Thêm vào BST

Báo xấu

35
lượt xem 6
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Bài giảng Cơ học lý thuyết: Chương 6 Chuyển động song phẳng của vật rắn, cung cấp cho người học những kiến thức như: Định nghĩa và mô hình vật rắn chuyển động song phẳng; Khảo sát chuyển động của toàn bộ vật rắn; Vận tốc và gia tốc của điểm thuộc vật rắn.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài giảng Cơ học lý thuyết: Chương 6 - Huỳnh Vinh

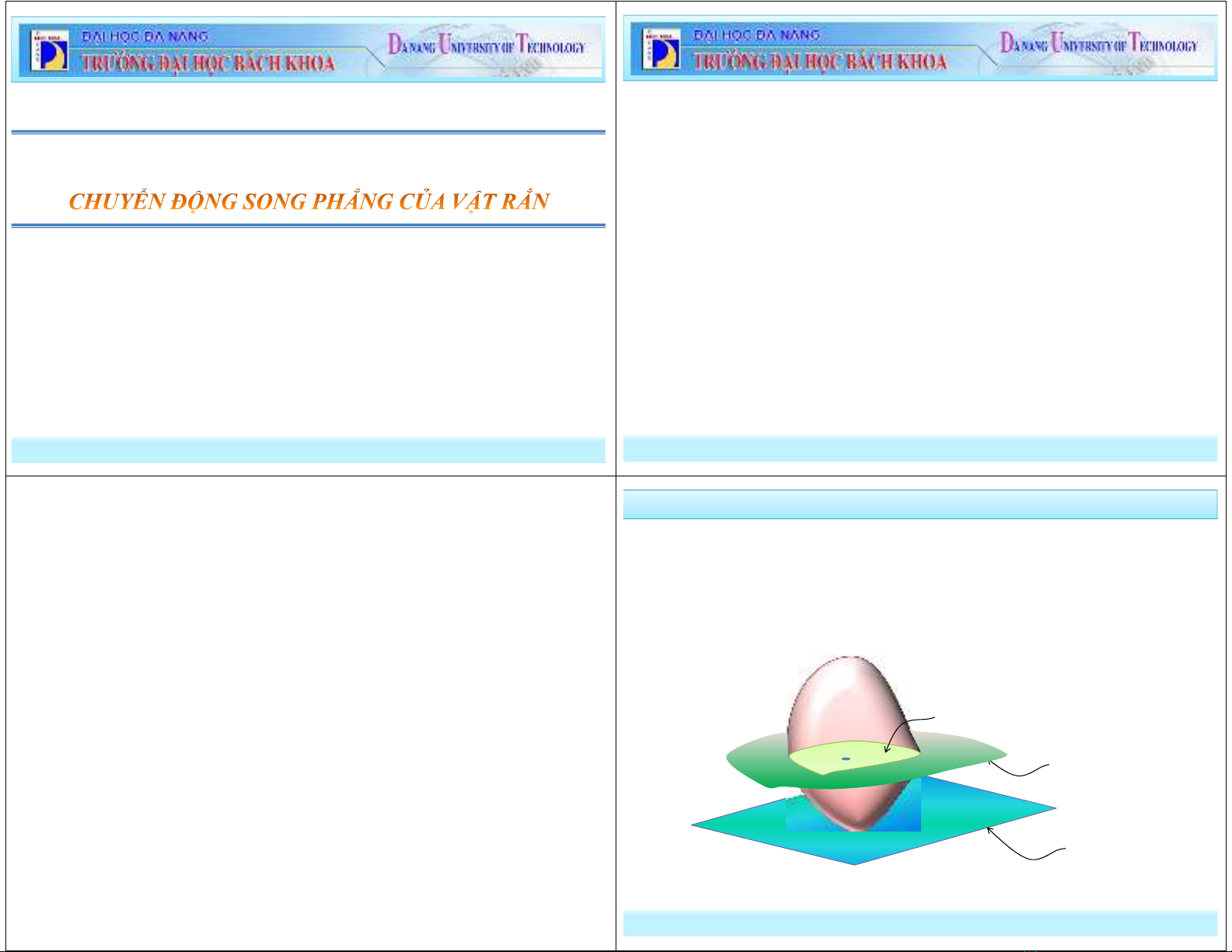
Chương 6 §1. Định nghĩa và mô hình vật rắn chuyển động song phẳng GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 489 GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 490 1. Định nghĩa Vật rắn chuyển động song phẳng khi khoảng cách từ mỗi điểm của nó đến một mặt phẳng quy chiếu cố định luôn luôn không đổi. + Mỗi điểm thuộc thiết diện của vật song song với mặt phẳng quy chiếu cố định chỉ chuyển động trong mặt phẳng chứa nó. Thiết diện (S) song song với (π0) M Mặt phẳng chứa quỹ đạo của M Mặt quy chiếu cố định (π0) GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 491
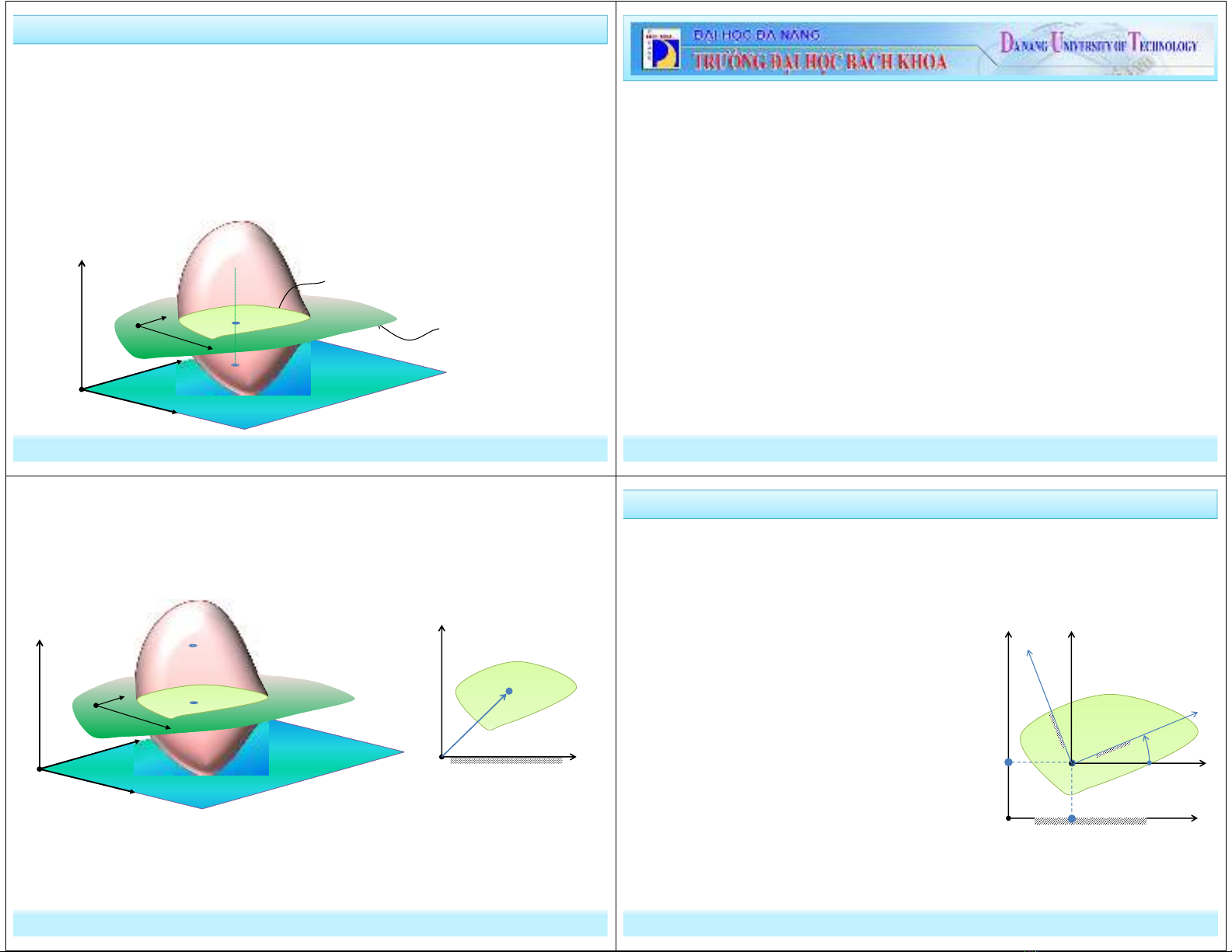
2. Mô hình vật rắn chuyển động song phẳng - Đoạn AB thuộc vật rắn vuông góc với pm(π0) chỉ có chuyển động tịnh tiến vì nó có phương không đổi. Chuyển động của AB đặc trưng bởi chuyển động của điểm bất kỳ thuộc nó. Ví dụ giao điểm của AB với thiết diện (S) song song với pm(π0). - Chuyển động của (S) trong mặt phẳng song song với pm(π0) đặc trưng §2. Khảo sát chuyển động của toàn bộ cho chuyển động của vật rắn. vật rắn A Thiết diện (S) song song với (π0) y O M Mặt phẳng chứa x quỹ đạo của M B Mặt quy chiếu cố định (π0) GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 492 GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 494 - Thiết diện (S) được gọi là mô hình phẳng của vật rắn chuyển động 1. Phương trình chuyển động của vật rắn song phẳng. - Muốn lập phương trình chuyển động toàn bộ vật rắn, ta chỉ cần lập phương trình chuyển động của thiết diện (S). 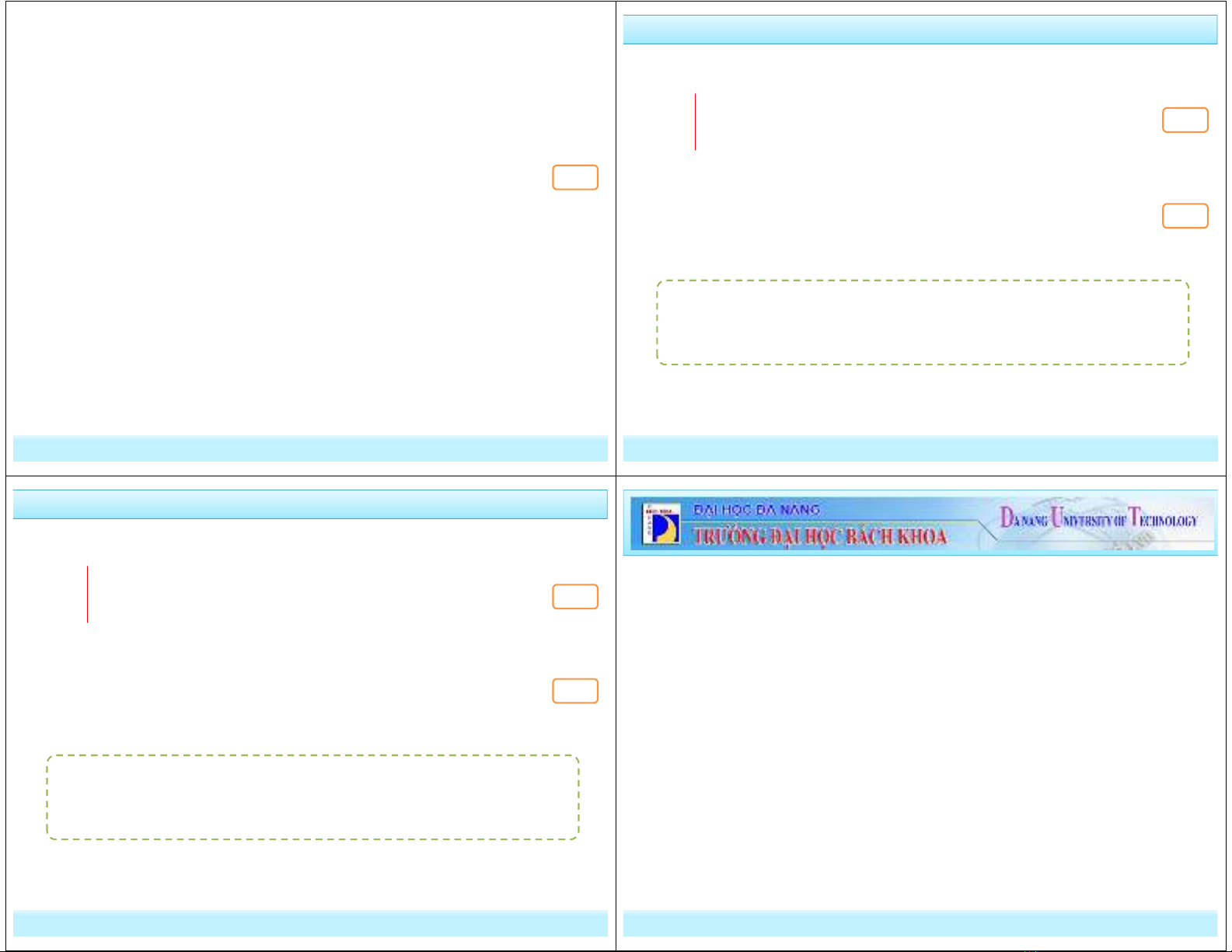y + Trong mặt phẳng chứa thiết diện (S): y y1 A . Lập hệ trục tọa độ cố định Oxy. y' . Qua một điểm A nào đó gọi là y M điểm cực trên thiết diện (S), lập hệ trục O M x' tọa độ Ax1y1 luôn luôn song song với (S ) x r hệ trục Oxy là hệ quy chiếu động. B x A ϕ (t ) O y A (t ) + (S) chuyển động quay tương đối x1 quanh cực A trong hệ quy chiếu Ax1y1, hệ quy chiếu Ax1y1 chuyển động tịnh O x tiến so với hệ trục quy chiếu cố định x A (t ) Oxy. GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 493 GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 495
+ Các thông số định vị (S) là tọa độ A(xA,yA) và góc ϕ thay đổi theo thời 3. Gia tốc của chuyển động của vật rắn gian. - Gia tốc chuyển động tịnh tiến của vật theo điểm cực A + Phương trình chuyển động: a Ax = ɺɺ x A (t )  x A = x A (t ) aA 6.4 a Ay = ɺɺ y A (t )   y A = y A (t ) ϕ (t ) = ϕ (t ) 6.1 - Gia tốc góc của vật quay quanh cực A – gia tốc góc song phẳng  sp ε sp (t ) = ϕɺɺ(t ) 6.5 - Hai phương trình đầu thể hiện chuyển động tịnh tiến của hệ tọa độ động Ax1y1 so với hệ trục tọa độ cố định Oxy (chuyển động tịnh tiến của vật rắn theo điểm cực A). - Phương trình thứ ba thể hiện chuyển động quay quanh cực A của (S) - Gia tốc của thành phần chuyển động tịnh tiến phụ thuộc vào việc chọn cực. - Gia tốc góc của thành phần chuyển động quay không phụ thuộc vào việc chọn cực. GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 496 GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 498 2. Vận tốc của chuyển động của vật rắn - Vận tốc chuyển động tịnh tiến của vật theo điểm cực A v Ax = xɺ A (t ) vA 6.2 v Ay = yɺ A (t ) §3. Vận tốc và gia tốc của điểm thuộc vật rắn - Vận tốc góc của vật quay quanh cực A – vận tốc góc song phẳng 6.3 ω sp (t ) = ϕɺ (t ) - Vận tốc của thành phần chuyển động tịnh tiến phụ thuộc vào việc chọn cực. - Vận tốc góc của thành phần chuyển động quay không phụ thuộc vào việc chọn cực GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 497 GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 499
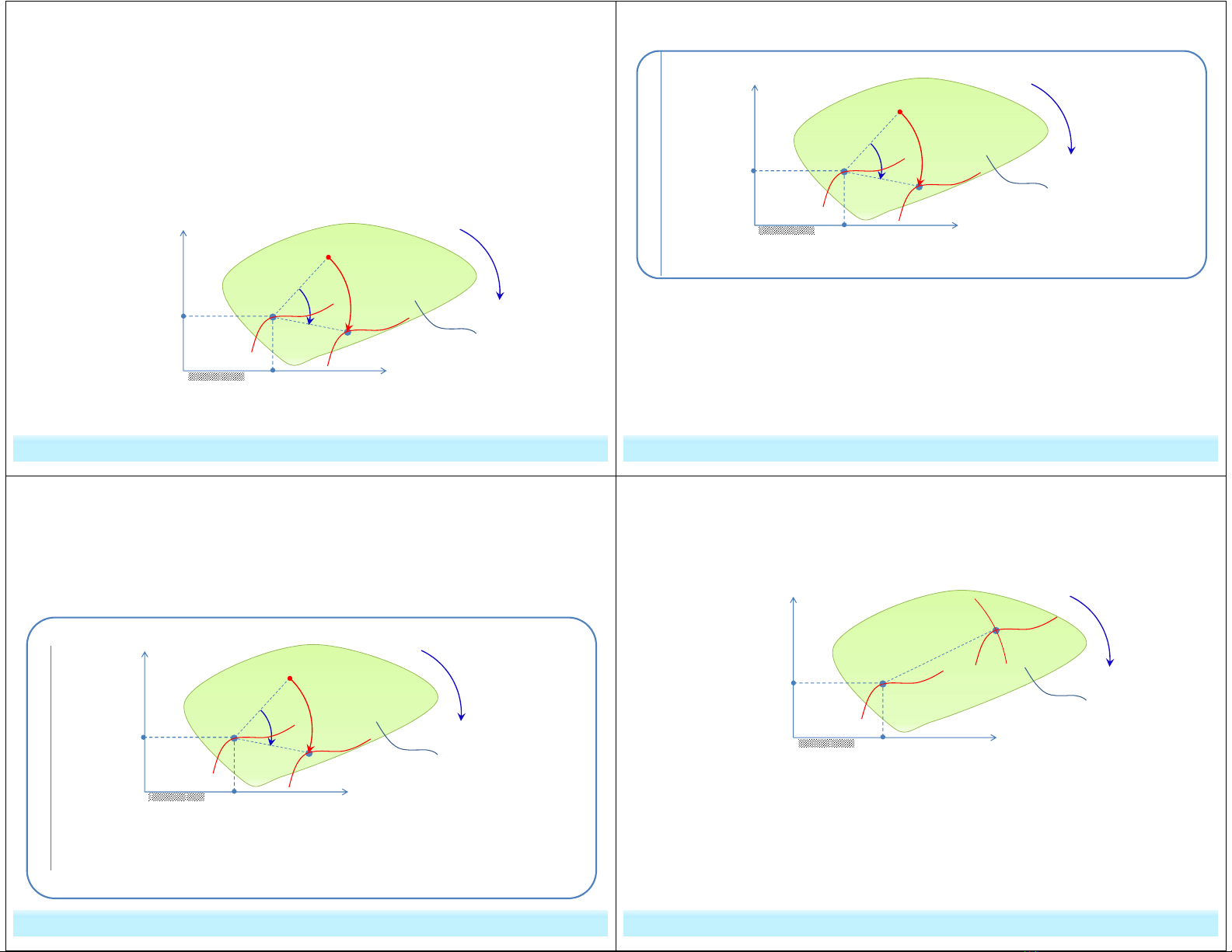
* Phân tích chuyển động của điểm M bất kỳ thuộc (S): (S) chuyển động tịnh tiến cùng cực O – M chuyển động trên (S) - Xét M là một điểm thuộc (S) – cố định so với (S), khi (S) chuyển y động song phẳng thì M chuyển động cùng với (S). Điểm M tham gia hai thành phần chuyển động: ϕ sp (t ) SƠ ĐỒ TOÁN + Chuyển động với (S) khi (S) chuyển động tịnh tiến cùng cực O (S ) s r (t ) ϕ sp + Chuyển động với (S) khi (S) chuyển động quay quanh cực O. O yO (t ) M Chuyển động (S) chuyển động song phẳng – M thuộc (S) R x tịnh tiến cùng cực O y xO (t ) ϕ sp (t ) sr (t ) = ϕ sp (t ).R (S ) ϕ sp s q (t ) O + Chuyển động của M trên (S) theo cung tròn tâm O bán kính R là yO (t ) M Chuyển động chuyển động tương đối. Phương trình chuyển động: sr (t ) = ϕ (t ).R R song phẳng x + Tưởng tượng dừng M lại trên (S), khi (S) chuyển động kéo theo M chuyển động. Chuyển động của M lúc này so với (x,y) là xO (t ) sq (t ) = ϕ sp (t ).R chuyển động theo. + Gia tốc Coriolis tại M luôn bằng 0 GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 500 GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 502 Về toán học, ta có thể xem điểm M chuyển động trên (S) với quỹ đạo là Với phân tích trên, quay lại sơ đồ cơ học, ta có kết luận về chuyển cung tròn tâm là cực O, bán kính OM; trong lúc (S) đang chuyển động động của điểm M thuộc (S) như sau: tịnh tiến cùng với cực O. y (S) chuyển động tịnh tiến cùng cực O – M chuyển động trên (S) M ϕ sp (t ) y R (S ) ϕ sp (t ) O yO (t ) Chuyển động (S ) s q (t ) ϕ sp song phẳng SƠ ĐỒ TOÁN O x yO (t ) M Chuyển động R xO (t ) x tịnh tiến cùng cực O xO (t ) + Chuyển động của M khi (S) chuyển động quay quanh cực O là chuyển động tương đối. sq (t ) = ϕ sp (t ).R + Chuyển động của M khi (S) chuyển động tịnh tiến cùng với cực O là chuyển động theo. 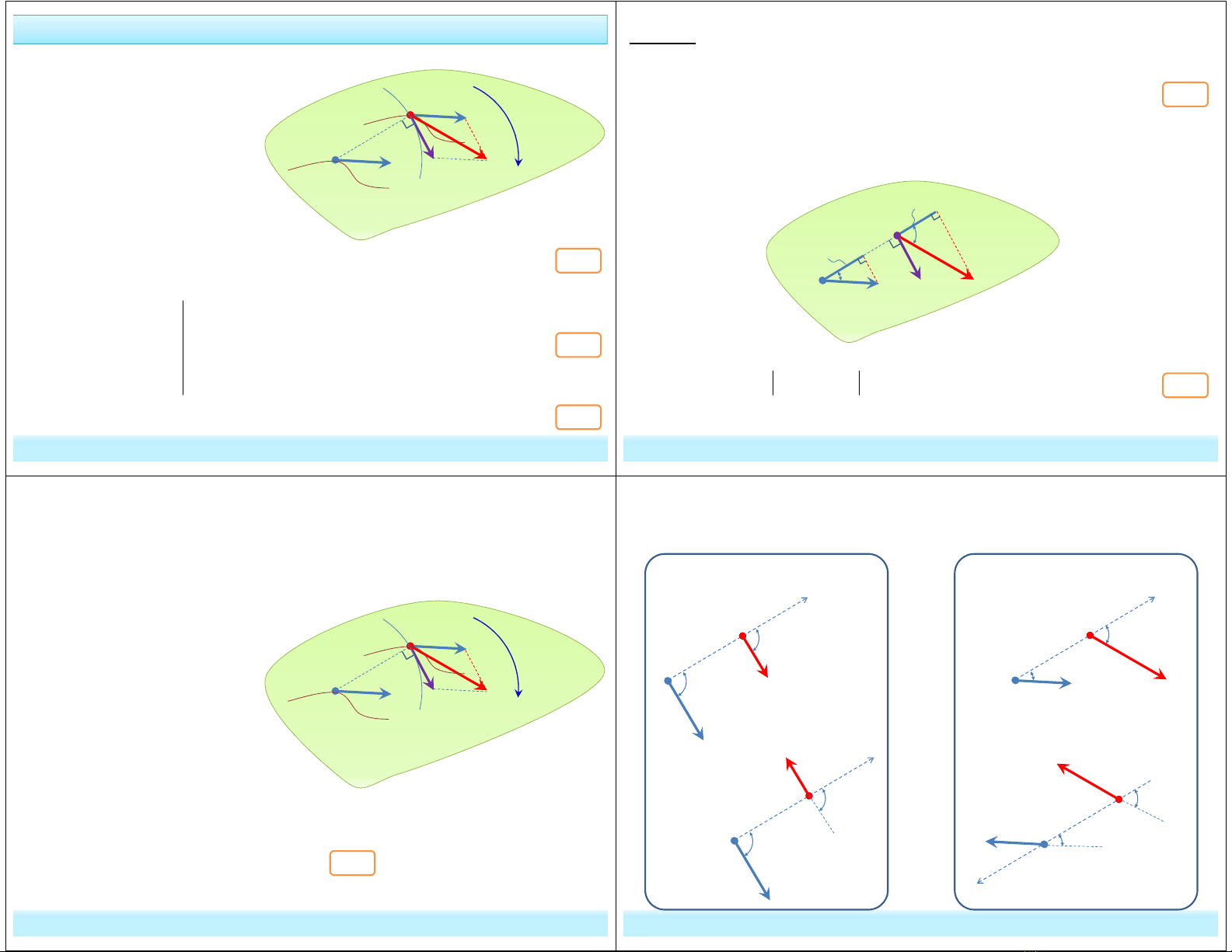GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 501 GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 503
1. Sự liên hệ vận tốc giữa hai điểm thuộc vật Chú ý: Vì có thể chọn điểm cực một cách tuỳ ý nên công thức liên hệ * Theo sơ đồ toán, dùng công thức hợp vận tốc: vận tốc của hai điểm A, B bất kỳ thuộc (S): vO v B = v A + v BA 6.9 M ω sp b. Định lý 2: Hình chiếu vận tốc của hai điểm bất kỳ thuộc hình phẳng vM = vMr + vMe R (S) chuyển động song phẳng lên trục qua hai điểm ấy thì bằng nhau. vO vM O vMO ω sp vB .cos β (S ) B β (S )  vMe = vO (Vận tốc của M khi (S) chuyển động tịnh tiến cùng với cực O) v A .cos α Mà  r 6.6 vB A α  vM = vMO (Vận tốc của M khi (S) chuyển động quay quanh cực O) v A v BA vMO (t ) = sɺr (t ) = ω sp (t ).MO Với vMO Theo chiều ω sp đối với O 6.7 vMO = MO.ω sp hc AB v A = hc AB v B ⇒ v A .cos α = v B .cos β 6.10 Nên vM = vO + vMO 6.8 GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 504 GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 506 a. Định lý 1: Vận tốc của điểm M thuộc (S) chuyển động song phẳng * Từ công thức v B = v A + v BA , chiều véc tơ vận tốc tại hai điểm bất kỳ có bằng tổng hình học vận tốc của điểm cực O và vận tốc của điểm M trong những trường hợp sau: chuyển động quay tương đối của hình phẳng (S) quanh điểm cực O. Cùng vuông góc với phương Cùng xuôi theo một chiều trục nối hai điểm nối hai điểm B B M vO β = 90 0 β < 90 0 R ω sp A A α < 90 0 α = 90 0 vB vB vO vA O vMO vM vA (S ) vB vB B β = 90 0 β < 90 0 B vA A α < 90 0 α = 90 0 vM = vO + vMO 6.8 A vA GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 505 GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 507
2. Tâm vận tốc tức thời và sự phân bố vận tốc - Tại thời điểm khảo sát mà ωsp= 0 thì tâm vận tốc tức thời P ở xa vô a. Tâm vận tốc tức thời: cùng. Chuyển động của vật lúc này được gọi là tịnh tiến tức thời. Khi * Định nghĩa: Điểm P thuộc mặt phẳng chứa hình phẳng (S) mà tại thời vật chuyển động tịnh tiến tức thời, véc tơ vận tốc tại mọi điểm là bằng điểm khảo sát có vận tốc bằng không, gọi là tâm vận tốc tức thời. nhau. Thật vậy, xét 2 điểm M, N bất kỳ. Chọn N làm cực, ta có: Gọi P là tâm vận tốc tức thời, thì: v P = 0 Chọn P làm cực, vận tốc tại M bất kỳ vM = v N + vMN thuộc (S): M v = v Mà ωsp= 0 nên vMN = 0 M MP (S ) vM = v P + vMP = vMP N Do đó: v = v M N Trong đó: ω sp = 0 ( S ) M vN vM = vMP = ω sp .PM vM ω sp P P GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 508 GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 510 - Tại thời điểm khảo sát, vận tốc tại M và vận tốc góc ωsp là xác định * Cách xác định tâm vận tốc tức thời P nên tồn tại duy nhất một tâm vận tốc tức thời P. TH1: Biết vận tốc 1 điểm, phương vận tốc điểm khác, phương vận tốc hai - Đường thẳng đi qua M bất kỳ mà vuông góc với vận tốc tại M chứa điểm khác nhau: tâm vận tốc tức thời P. Tâm vận tốc tức thời P luôn nằm về phía đường thẳng đối với M mà vận tốc tại M quay quanh P theo chiều của ωsp, B PM = vM /ωsp. (S ) A M vA vM B (S ) vB (S ) A ω sp vA ω sp P vA v ω sp ω sp = = B vM = ω sp .PM vA PA PB P ω sp = PA ⇒ vB = ω sp .PB P GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 509 GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 511
TH2:Biết hai véc tơ vận tốc v A / / v B vB vB B B vB vB (S ) (S ) B (S ) B (S ) v A < vB vA A vA A vA A vA A ω sp (ω sp = 0) P P→∞ vB B (S ) vB v ω sp = = A PB PA Vật chuyển động tịnh tiến tức thời v A = v B vA A vB − v A ω sp = AB P Tại thời điểm đang xét mà v A = v B thì vật chuyển động tịnh tiến tức thời. GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 512 GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 514 TH3: Đĩa tròn lăn không trượt trên vật cố định vB vB B (S ) B (S ) ω sp vB P B O vO A A A vA vA R vA vB v v (S ) ω sp = A = O = ω sp PB PA R vB v ω sp = = A P vB PB PA B (S ) vB + v A Cố định ω sp = P AB A vA GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 513 GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 515
b. Phân bố vận tốc khi biết tâm vận tốc tức thời P: a. Định lý: Gia tốc của điểm M thuộc (S) chuyển động song phẳng bằng tổng hình học gia tốc của điểm cực O và gia tốc của điểm M trong chuyển động quay tương đối của hình phẳng (S) quanh điểm cực O. E τ n a M = aO + a MO + a MO 6.11 vB vE B D (S ) n M aO vD a MO A vA ε sp C τ vC a MO  v B = ω sp .PB O aO   v D = ω sp .PD n ∈ MO , M → O  v = ω .PE a MO 6.12 (S ) ω sp  E sp n a MO = ω sp2 .MO P aτMO (t ) = ɺɺ sr (t ) = ε sp (t ).MO  v A = ω sp .PA τ a MO ⊥ MO , theo chiều ε sp đối với O  6.13  vC = ω sp .PC τ a MO = ε sp .MO GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 516 GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 518 3. Sự liên hệ gia tốc của hai điểm thuộc vật rắn * Lưu ý khi vật chuyển động tịnh tiến tức thời: * Theo sơ đồ toán: a M = a Mr + a Me + a Mc vI ω sp = 0 i a Mc = 0 vO i a Me = aO I aO ε sp τ n O i a Mr = a MO + a MO aO τ n Do đó: a M = aO + a MO + a MO τ a IO aI (S ) n M aO a MO + Vận tốc tại các điểm là như nhau: ε sp ω sp = 0⇒ v IO = 0 τ v I = vO + v IO     → v I = vO , ∀ I O a MO aO + Gia tốc mọi điểm bằng nhau khi và chỉ khi εsp = 0: (S ) n τ n ω sp = 0⇒ a IO =0 a I = aO + a IO + a IO ε  τ = 0⇒ a = 0 → a I = aO , ∀ I sp IO GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 517 GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 519
* OA chuyển động quay quanh O Có chiều như hình vẽ 30 0 vA ω0 v A = ω 0 .OA = 3 (m/s) vA H * AB chuyển động song phẳng: O A ε0 60 0 Để xác định vận tốc tại B, ta có thể dùng 2 dạng công thức: D + Công thức chiếu ▲ vD Có chiều như hình vẽ 60 0 BÀI TẬP CHƯƠNG 6 SINH VIÊN CẦN GIẢI QUYẾT vB vB v .cos 30 0 vB = A = 3 3 (m/s) B r Các đại lượng cần tìm trong bài toán song phẳng cos 60 0 - Tìm vận tốc góc hình phẳng, tìm vận tốc của điểm bất kỳ thuộc vật phẳng. - Tìm gia tốc góc hình phẳng, tìm gia tốc của điểm bất kỳ thuộc vật phẳng. I GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 520 GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 522 Bài tập 6.1 + Tâm vận tốc tức thời là H Cho cơ cấu sau, tại thời điểm khảo sát, tay quay OA có ω0 = 1 (rad/s), 30 0 ε0 = 1 (rad/s2), OA = 3r = 3 (m), AB = 4 (m), bánh xe B lăn không trượt Có chiều như hình vẽ ω0 vA trên đường ngang cố định. Thanh OA song song với mặt đường lăn của ω AB v 3 H ω AB = A = (rad/s) O A bánh xe, yêu cầu xác định: HA 2 ω0 1. v A , v B , v D A ε0 60 0 O 2. ω AB , ω b . xe Có chiều như hình vẽ ω AB ε0 60 0 3. a A , a B , ε AB , ε bx vB D▲ v B = ω AB .HB = 3 3 (m/s) vD D 60 0 ▲ vB B r 60 0 B r I GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 521 GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 523
* Bánh xe chuyển động song phẳng với tâm vận tốc tức thời là I: * AB chuyển động song phẳng, trong đó phương của gia tốc tại B đã biết. Chọn A làm cực: Có chiều như hình vẽ 30 0 τ n vD ω0 a B = a A + a BA + a BA ω 0 a n A v D = 2.v B = 6 3 (m/s) vA τ n τ n O A H ⇒ a B = a A + a A + a BA + a BA (*) O A 60 0 Có chiều như hình vẽ + Chiếu (*) lên trục AB: ε0 ωbx aτA v ε0 60 0 ω AB ωbx = B = 3 3 (rad/s) − a B .cos 60 0 = aτA .cos 30 0 + a An .cos 60 0 − a BA n ε AB r n ω AB n a BA D▲ a BA τ ( gt ) ⇒ aB = − aτA .tan 60 0 − a An a BA vD cos 60 0 60 0 60 0 2 ω AB . AB aB( gt ) ⇒ aB = τ 0 − a A .tan 60 − a A n B r vB cos 60 0 ε bx B r ⇒ a B = 3(5 − 3) (m/s 2 ) > 0 I ωbx I Có chiều như đã giả thiết ⇒ aB a B = 3(5 − 3) (m/s 2 ) GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 524 GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 526 * OA chuyển động quay quanh O + Chiếu (*) lên trục thẳng đứng hướng lên: a A = aτA + a An 0 = − aτA + a BA τ .cos 60 0 + a BA n .cos 30 0 ω 0 a n A A aτA , a An có chiều như hình vẽ O aτA ⇒ a BA τ = 0 n − a BA .tan 60 0 60 0 cos 60 a A = ε 0 .OA = 3 (m/s ) ε0 τ 2 aτA ⇒ a BA τ = 6 − 9 3 (m/s 2 ) < 0  n 2 2 a A = ω0 .OA = 3 (m/s ) ▲ D τ Có chiều ngược với chiều đã giả thiết ⇒ a BA a An aτBA = 9 3 − 6 (m/s 2 ) A 60 0 450 B + Gia tốc góc của thanh AB r aτA Có chiều như hình vẽ ε AB aτBA 9 3 − 6 aA ε AB = = (rad/s 2 ) AB 4 a A = 3 2 (m/s 2 ) GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 525 GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 527
+ Bánh xe chuyển động song phẳng, tâm vận tốc tức thời là I. * OA chuyển động quay quanh O vC Theo thời gian t, ta luôn có: Có chiều như hình vẽ ω BC d ωbx (t ) 1 dv B (t ) 1 vA ε bx (t ) = = = a B (t ) v A = ω 0 .OA = 1 (m/s) P C dt r dt r Tại thời điểm đang xét * BD chuyển động song phẳng, B vB tịnh tiến tức thời: Có chiều như hình vẽ vA A ε bx a 3(5 − 3) vD = vB = v A ε bx = B = = 3(5 − 3) (rad/s 2 )  ω0 60 0 r 1  v D = v B = v A = 1 (m/s) D vD ω = 0  BD O ε0 * Lưu ý: đây là cách tính gia tốc góc của vật lăn không trượt trên vật cố định. * BC chuyển động song phẳng với tâm vận tốc tức thời là P: Có chiều như hình vẽ ω BC v Có chiều như hình vẽ ω BC = B = 2 (rad/s) vC PB vC = ω BC .PC = 3 (m/s) GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 528 GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 530 Bài tập 6.2 * OA chuyển động quay quanh O Cho hệ ở vị trí như hình vẽ. Tại thời điểm khảo sát, tay quay OA có C a A = a An + a τA ω0 = 1 (rad/s), ε0 = 1 (rad/s2), con trượt tại C trượt theo phương OA, con trượt tại D trượt theo phương vuông góc với OA. B Có chiều như hình vẽ Biết OA = AB =BC = 1 (m), AD = 2 (m). Yêu cầu xác định: a τA τ aτA a A = ε 0 . AO = 1 (m/s 2 ) 1. v A , v B , v D , vC An aA 60 0 2. ω BC , ω BD C Có chiều như hình vẽ ω0 a An n D 3. a A , a B , aC a A = ω 02 . AO = 1 (m/s 2 ) O ε0 B 4. ε BC , ε BD A A aτA 0 2 ω0 60 a A = 2 (m/s ) 450 D O ε0 a An aA GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 529 GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 531
* AD chuyển động song phẳng - tịnh tiến tức thời, chọn A làm cực: + Chiếu phương trình véc tơ (*) lên trục thẳng đứng hướng lên: τ τ τ 0 = 0 − a An + a DA .cos 30 0 a D = a A + a DA = a τA + a An + a DA (*) a An 2 3 + Điểm D có quỹ đạo là đường ⇒ a DA τ = 0 = (m/s 2 ) > 0 cos 30 3 ngang tại D, nên gia tốc tại D đã C C biết phương, chiều giả thiết: + Thanh AD chưa biết εAD B Do đó: B τ nên chiều của a DA được giả thiết: aτA aτA τ ( gt ) τ ( gt ) An aDA τ Có chiều như đã giả thiết An aDA aA aDA aA ω0 60 0 τ 2 3 ω0 60 0 D aDA = (m/s2 ) D 3 O ε0 O ε0 aD( gt ) aD( gt ) GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 532 GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 534 + Chiếu phương trình véc tơ (*) lên trục AD: τ + Với A làm cực, thì ta đã xác định được aDA , do đó gia tốc góc của thanh AD được xác định như sau: a D .cos 30 0 = aτA .cos 30 0 + a An .cos 60 0 ⇒ a D = aτA + a An .tan 30 0 C 3+ 3 ⇒ aD = (m/s 2 ) > 0 C B 3 Do đó: B aτA τ aτA A ε AD aDA Có chiều như đã giả thiết τ ( gt ) a An 60 0 aD A aDA ω0 3+ 3 a An D aD = (m/s 2 ) ω0 60 0 3 O ε0 D ε0 aD O aD( gt ) Có chiều như hình vẽ ε AD = ε BD aτDA 3 ε BD = = (rad/s2 ) AD 3 GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 533 GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 535
• Chọn cực là D: y * BC chuyển động song phẳng, chọn B làm cực: τ ( gt ) τ τ n aCB aC( gt ) a B = a D + a BD a By ( gt ) aC = a B + aCB + aCB x τ n τ ⇒ a Bx + a By = a D + a BD (**) ⇒ aC = a Bx + a By + aCB + aCB (***) n a Bx ( gt ) aCB C B B τ A aBD 30 0 a Bx ε AD 60 0 ω BC + Chiếu (**) lên trục x: D SV giải tiếp a By a Bx = a D − aτBD .cos 60 0 = a D − (ε BD .BD ).cos 60 0 aD 3+ 3 3 1 6− 3 = − .3. = (m/s 2 ) > 0 3 3 2 6 Chiều như đã giả thiết a Bx x 6 − 3 aB = (m/s 2 ) 6 GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 536 GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 538 + Chiếu (**) lên trục y: y Bài tập 6.3 a By = − aτBD .cos 30 0 = − (ε BD .BD ).cos 30 0 Cho hệ ở vị trí như hình vẽ. Biết OA = BC = 40 (cm), BD = 80 (cm), 3 3 3 x BD vuông góc với BC. Tại thời điểm khảo sát, tay quay OA có ω0 = 3 =− .3. = − (m/s 2 ) < 0 (rad/s), ε0 = 1 (rad/s2), con trượt tại C trượt theo phương OA, con trượt 3 2 2 a Bx tại D trượt theo phương vuông góc với OA. Yêu cầu xác định: B τ A 1. v A , v B , v D aBD 2. ω BC , ω BD C ε AD a By 60 0 3. a A , a B , ε BC , ε BD D B Ngược với chiều đã giả thiết a By y 3 aD a B = (m/s 2 ) A 2 ω0 60 0 D 0 Hợp với trục x góc α = 64,37 aB O ε0 a B = ( a Bx ) 2 + ( a By ) 2 = 1, 66 (m/s 2 ) GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 537 GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 539
vC * BA chuyển động song phẳng, chọn A τ n * OA chuyển động quay quanh O làm cực: a B = a A + a BA + a BA PBC ω0 → v A C Do chuyển động tịnh tiến tức thời, nên: n * BD chuyển động song phẳng: a BA =0 C τ ( gt ) v A → vD = vB = v A Vì vậy: aBA B vB τ BD chuyển tịnh tiến tức thời a B = a A + a BA vA τ aBx ( gt ) ω BD = 0 A ⇒ a B = a τA + a An + a BA B * BC chuyển động song phẳng: aτA τ ( gt ) aDA 0 τ A ω0 60 30 0 D vD ⇒ a Bx + a By = a τA + a An + a BA aBy ( gt ) n  vC aA PBC →  60 0 D ω BC Chiếu lên phương ngang và phương ω0 30 0 O ε0 thẳng đứng, ta có: O ε0 aD( gt )  a Bx  a Bx ⇒  y ⇒ y  a B  a B GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 540 GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 542 * OA chuyển động quay quanh O aCgt * BC chuyển động song phẳng, ε 0 → a A = a An + a τA chọn C làm cực: * AD chuyển động song phẳng, chọn A C làm cực: n τ n C aBC a D = a A + a DA + a DA τ ( gt ) aBC Do chuyển động tịnh tiến tức thời, nên: B aBx ( gt ) n a DA =0 τ B A Vì vậy: a D = a A + a DA aτA τ ( gt ) τ n aDA a B = aC + a BC + a BC τ A aBy ( gt ) 60 0 D ⇒ a D = a τA + a An + a DA n n ω0 30 0 aA ⇒ a Bx + a By = aC + a τBC + a BC (*) Chiếu lên phương AD và phương ω 60 0 D 0 30 0 O ε0 vuông góc AD n B → C aD( gt ) Với: a BC O ε0 n a BC = (ω BC ) 2 .BC aD aD ⇒  τ ⇒  τ  aC  aC Chiếu (*) lên hai phương khác nhau bất kỳ: ⇒  τ ⇒  τ  a DA  a DA ⇒ ε AD  a BC  a BC ⇒ ε BC GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 541 GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 543
Bài tập 6.4 * BC chuyển động song phẳng, I là tâm vận tốc tức thời Cho hệ ở vị trí như hình vẽ. Biết OA = 2.AB = BC =AD = 2 (m), BC BI IC 2 P α = 30 0 = = = = 4 ω0 = 1 (rad/s), ε0 = 1 (rad/s2). Yêu cầu xác định: sin 30 0 sin135 0 sin150 1 / 2 α ω BD 1. v A , v B , vC , v D  IB = 2 2 (m) 2. ω BC , ω BD B ⇒ B vB A  IC = 6 − 2 (m) A 3. a , a , a , a , ε , ε A D B C BC BD vA C vD 450 60 0 450 60 0 C ω0 α vC ω0 D D ε0 ε0 O ω BC O I Chiều như hình vẽ Chiều như hình vẽ ω BC v 3 6 vC 3− 3 ω BC = B = == (rad/s) vC = ω BC .IC = (m/s) IB 2 2 4 2 GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 544 GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 546 * OA chuyển động quay quanh O cố định: * OA chuyển động quay quanh O cố định: P Chiều như hình vẽ a A = a An + a τA vA v A = ω 0 .OA = 2 (m/s) Có chiều như hình vẽ Có chiều như hình vẽ ω BD a τA τ a An n * BD chuyển động song phẳng, P là tâm a A = ε 0 . AO = 2 (m/s 2 ) a A = ω 02 . AO = 2 (m/s 2 ) B vận tốc tức thời vB B A vA A A τ ( gt ) Chiều như hình vẽ C vD aτA aDA ω BD v 450 450 aτA ω BD = A = 1 (rad/s) 60 0 C n PA 450 60 0 aDA aDgt ω0 D ω0 a An ε0 a An aA D Chiều như hình vẽ vD O ε0 v D = ω BD .PD = 2 3 (m/s) a A = 2 2 (m/s 2 ) O Chiều như hình vẽ * BAD chuyển động song phẳng, chọn A làm cực: vB τ n v B = ω BD .PB = 3 (m/s) a D = a τA + a An + a DA + a DA (*) GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 545 GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 547
Chiếu (*) lên trục BD: * BAD chuyển động song phẳng, chọn D làm cực: τ n a D .cos 60 0 = aτA .cos 30 0 + a An cos 60 0 − a DA n a B = a D + a BD + a BD (**) Chiếu (**) lên trục x,y: y ⇒ a D .cos 60 0 = aτA .cos 30 0 + a An cos 60 0 − ω AD 2 . AD  a Bx = a D .cos 30 0 − aτBD .cos 60 0 + a BD n .cos 30 0 ⇒ a D = aτA .tan 60 0 + a An − ω AD 2 . AD / cos 60 0  y 0 τ 0 n 0 x  a B = a D .sin 30 − a BD .sin 60 − a BD .sin 30 ⇒ a D = 2. 3 + 2 − 1.2.2 = 2 3 − 2 (m/s 2 ) > 0  a Bx = (2 3 − 2).cos 30 0 − 1.3.cos 60 0 + 12.3.cos 30 0 ⇒ Do đó: y 0 0 2  a B = (2 3 − 2).sin 30 − 1.3.sin 60 − 1 .3.sin 30 0 ε AD B B n aBD Có chiều như đã giả thiết A τ ( gt ) A aD aDA aτA τ aD = 2 3 − 2 (m/s2 ) C n C aBD 450 60 0 aDA aD  x 3+ 3 45 0 60 0 aD 2 a An  a B = (m/s ) ω0 ⇒ 2 ω0 D D ε0  a y = − ( 3 + 5 ) (m/s 2 ) ε0 O  B 2 O GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 548 GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 550 Chiếu (*) lên trục ngang chiều hướng sang phải: 0 Hợp với trục x góc α = −54,89 a D .cos 30 0 = aτA + a DA τ .cos 60 0 − a DA n .cos 30 0 aB a B = ( a Bx ) 2 + ( a By ) 2 = 4,11 (m/s 2 ) 3 1 3 ⇒ (2 3 − 2). τ = 2 + a DA . − 2. ⇒ a DA τ = 2 (m/s 2 ) > 0 Phân tích: a B = a Bx + a By , các véc tơ thành phần có chiều như hình vẽ, với 2 2 2 Do đó:  x 3+ 3 ε AD  a B = (m/s 2 ) y 2 τ Có chiều như đã giả thiết B  aDA τ A τ  a y = ( 3 + 5 ) (m/s 2 ) x aDA = 2 (m/s2 ) aτA aDA  B 2 C n B 450 60 0 aDA aD aBx ω0 a An D C aBy Có chiều như hình vẽ ε0 450 O ε AD aτAD ε AD = =1 (rad/s2 ) AD GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 549 GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 551
* BC chuyển động song phẳng, chọn B làm cực: Do đó: τ n τ n aC = a B + aCB + aCB = a Bx + a By + aCB + aCB (***) Có chiều như đã giả thiết τ y aCB 2 6 + 10 2 − 3 Có chiều như hình vẽ τ aCB = (m/s2 ) n 2 aCB 2 6 3 x y n aCB = ωCB .CB = .2 = (m/s2 ) 16 4 Có chiều như hình vẽ B x τ ( gt ) ε CB τ aCB 2 6 + 10 2 − 3 aCB n aBx ε CB = = (rad/s2 ) aCB CB 4 B τ ( gt ) Chiếu (***) lên trục CB: C 0 aBy aCB n aBx 45 aCB 0 x y 0 n aC cos 45 = ( a − a ) cos 45 − a C B B CB aC( gt ) 450 aBy ⇒ aC = ( a Bx − a By ) − aCB n / cos 450 aC 4+3 2 ω BC ⇒ aC = − (m/s 2 ) < 0 4 ε CB ω BC GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 552 GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 554 Do đó: Bài tập 6.5 Có chiều ngược với chiều đã giả thiết Cho cơ hệ tại thời điểm khảo sát có vị trí như hình vẽ sau: aC 4+3 2 y OA = 20 (cm) aC = (m/s2 ) R = 10 (cm) 4 x AB = l = 40 (cm) ω OA ε OA Chiếu (***) lên trục y: τ Tại thời điểm khảo sát: A 0 = 0 − a By + ( aCB n + aCB ) cos 450 B O τ ( gt ) n aBx ωOA = ω0 = 2 (rad/s) ⇒ aCB = a / cos 45 − a τ y 0 n aCB aCB H B CB C ε OA = ε 0 = 0 (rad/s 2 ) 2R 3+5 3 450 aBy ⇒ aCB τ = 2− 2 4 aC Xác định: B 2 6 + 10 2 − 3 ⇒ aCB τ = (m/s 2 ) > 0 R 2 1. vB , ω AB , a B , ε AB ω BC 2. ωbx , ε bx , a I 3. a H I GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 553 GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 555
Bài giải: 1.1. vB , ω AB a τA Do B chuyển vị thẳng, nên phương vận tốc của B như hình vẽ. ω OA ε OA ω AB vA v PB 20 3 a An = B ⇒ vB = .v A = .40 = 40 (cm/s) P ε AB PA PB PA 40 3 / 2 3 A α O vB 40 3 3 v B = ω AB .PB ⇒ ω AB = = =2 (rad/s) PB 20.3 3 2R n 1.2. a B , ε AB vA a BA B aB n τ Chọn A làm gốc: a B = a A + a BA+ a BA (*) τ vB a BA R ∈ AB , B → A n B aB vB a BA n 2 160 a BA = BA.ω BA = (cm/s 2 ) 3 I ω bx ⊥ AB , chiều giả thiết như hình vẽ. a τBA τ ε bx a BA = ? I GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 556 GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 558 * Xét thanh AB chuyển động song phẳng: Giả thiết chiều của a B như hình vẽ. Chiếu (*) lên phương AB: ⊥ OA, theo chiều ωOA vA a B .cos α = a An .cos α − a BA n v A = ω OA .OA = 40 (cm/s) n a BA 160 ⇒ a B = a An − = 80 − = 18, 416 (cm/s 2 ) cos α 3 a A = a An + a τA . Vì ε OA = 0 ⇒ a τA = 0 nên: a A = a An 3 2 Chiều thật của a B như chiều đã giả thiết. ∈ OA, A → O a An n 2 a A = OA.ω OA = 80 (cm/s 2 ) Chiếu (*) lên phương vuông góc với AB: τ a B .sin α = a An .sin α − a BA ⇒ a BA τ = a An .sin α − a B .sin α ⇒ a BA τ = ( a An − a B ) sin α = (80 − 18, 416).0,5 = 30, 792 (cm/s 2 ) τ Chiều thật của a BA như chiều đã giả thiết. GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 557 GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 559
aτ 30, 792 3. a H ε AB . AB = aτBA ⇒ ε AB = BA = = 0, 7698 (cm/s 2 ) n τ AB 40 Chọn B làm gốc: a H = a B + a HB + a HB (***) H Y τ a HB τ n τ n Chiều hợp chiều với a BA như hình vẽ. Chiều thật a B , a HB, a HB như hình vẽ, với: a HB B aB 2. ωbx , ε bx , a I a B = R.ε bx aI vB 40 3 4 3 ωbx = = = =2,3094 (rad/s) n a HB = R.ωbx2 IB 3.10 3 X ω bx I ε d ωbx d vB 1 dvB 1 τ a B aτHB = R.ε bx bx ε bx = = ( )= = .a B = dt dt BI R dt R R a Bτ Lưu ý: Với B là tâm của bánh xe thì ε bx = Chiếu (***) lên trục X,Y: R a 18, 416 a HX = a B + aτHB = R.ε bx + R.ε bx = 2 R.ε bx = 2 a B ε bx = B = = 1,8416 (rad/s 2 ) R 10 n a HY = − a HB = R.ωbx2 Chiều ωbx , ε bx như hình vẽ. GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 560 GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 562 * Lưu ý: Sự phân bố độ lớn thành phần gia tốc theo phương X của Y τ những điểm thuộc IH. H Y Chọn B làm gốc:a I = a B + a IBn + a IB (**) τ + Đoạn BH theo chiều từ B đến H: K a KB n τ aB Chọn B làm cực, xét điểm K cách B đoạn y: a KB B a Chiều thực a B , a IBn , a IB như hình vẽ, với: B n τ n aQB B a K = a B + a KB + a KB (1) a B = 18, 416 (cm/s 2 ) a IBn = a I τ τ aQB a IB X n a IB = R.ωbx2 = 53,333 (cm/s 2 ) X Chiếu (1) lên phương X, ta có: ω bx I ε I ε bx aτIB = R.ε bx = 10.1,8416 = 18, 416 (cm/s 2 ) bx a KX = a B + aτKB = R.ε bx + y.ε bx = ( R + y )ε bx H Y a HX = 2 a B + Đoạn BI theo chiều từ B đến I: Chiếu (**) lên trục X, Y: Chọn B làm cực, xét điểm Q cách B đoạn y: B  a IX = a B − aτIB = 18, 416 − 18, 416 = 0 (cm/s 2 ) n τ a B = a BX aQ = a B + aQB + aQB (2)  n 2  a IY = a IB = 53,333 (cm/s ) Chiếu (2) lên phương X, ta có: X Vậy: a I = a IBn τ aQX = a B − aQB = R.ε bx − y.ε bx = ( R − y )ε bx I ε bx GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 561 GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 563
Bài tập 6.6 * Xét thanh BD chuyển động song phẳng: Cho cơ hệ sau, với OA = 12 (cm), AD = AB ⊥ OA, chiều theo ωOA . Tại thời điểm khảo sát: vA v A = OA.ωOA = 12.3 = 36 (cm/s) C ωOA = 3 (rad/s) ε OA = ε 0 = 0 (rad/s 2 ) B a A = a An + a τA = 30 0 BC ⊥ BD , OAD a τA = 0 vì ε OA = 0 ∈ OA, A → O Xác định: a An n 2 A a A = OA.ωOA = 12.32 = 108 (cm/s 2 ) 1. vB , a B 2. vC , ω BC 30 0 1. vB , a B ωOA Do D chuyển động thẳng theo phương ngang, nên thanh BAD O chuyển động tịnh tiến tức thời: AD = AB = 8 3 (cm) D vB = v A = vD ⇒ vB = v A = vD = 36 (cm/s) GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 564 GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 566 Bài giải: Y Do thanh BAD chuyển động song phẳng, chọn A làm gốc, ta có: n τ ω BC vC vC aB = a A + aBA + aBA ω BC n P C P C Trong đó: aBA = 0 vì ωBA = 0 (BAD chuyển động tịnh tiến tức thời) τ Do đó: aB = a A + aBA (1) B vB B vB X τ τ τ τ a BA a BA Xác định aBA thì cần biết ε BA . Giả thiết chiều aBA như hình vẽ. n aBA ε BA = ε BD vA vA n τ τ A A Ta có: aD = a A + aDA + aDA = a A + aDA (2) y a An a An = a A n 30 0 n τ 30 0 τ Trong đó: aDA = 0 vì ωDA = 0 (BAD chuyển động tịnh tiến tức thời) a DA a DA a DA τ ωOA ωOA Do đó: aD = a A + aDA (3) O O x vD τ τ vD Xác định aDA thì cần biết ε DA . Giả thiết chiều aDA như hình vẽ. D D GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 565 GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bộ Slide 567