ĐỔI BIẾN TRONG TÍCH PHÂN KÉP
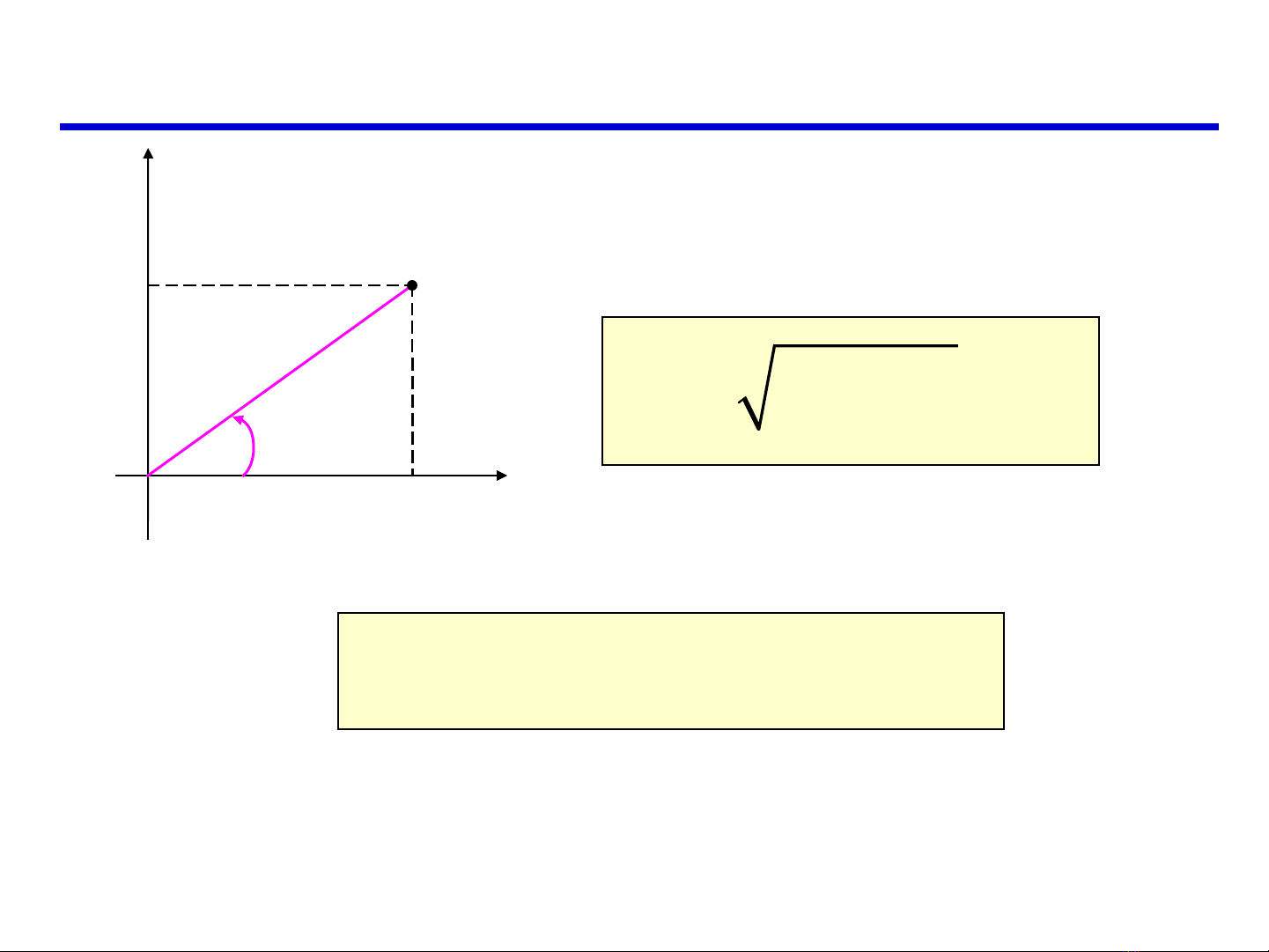
TỌA ĐỘ CỰC
M
y
r
x
[0,2 ] [ , ]
ϕ π ϕ π π
−� �ha y
cos , sin x r y r
ϕ ϕ
= =
2 2
0r x y= +
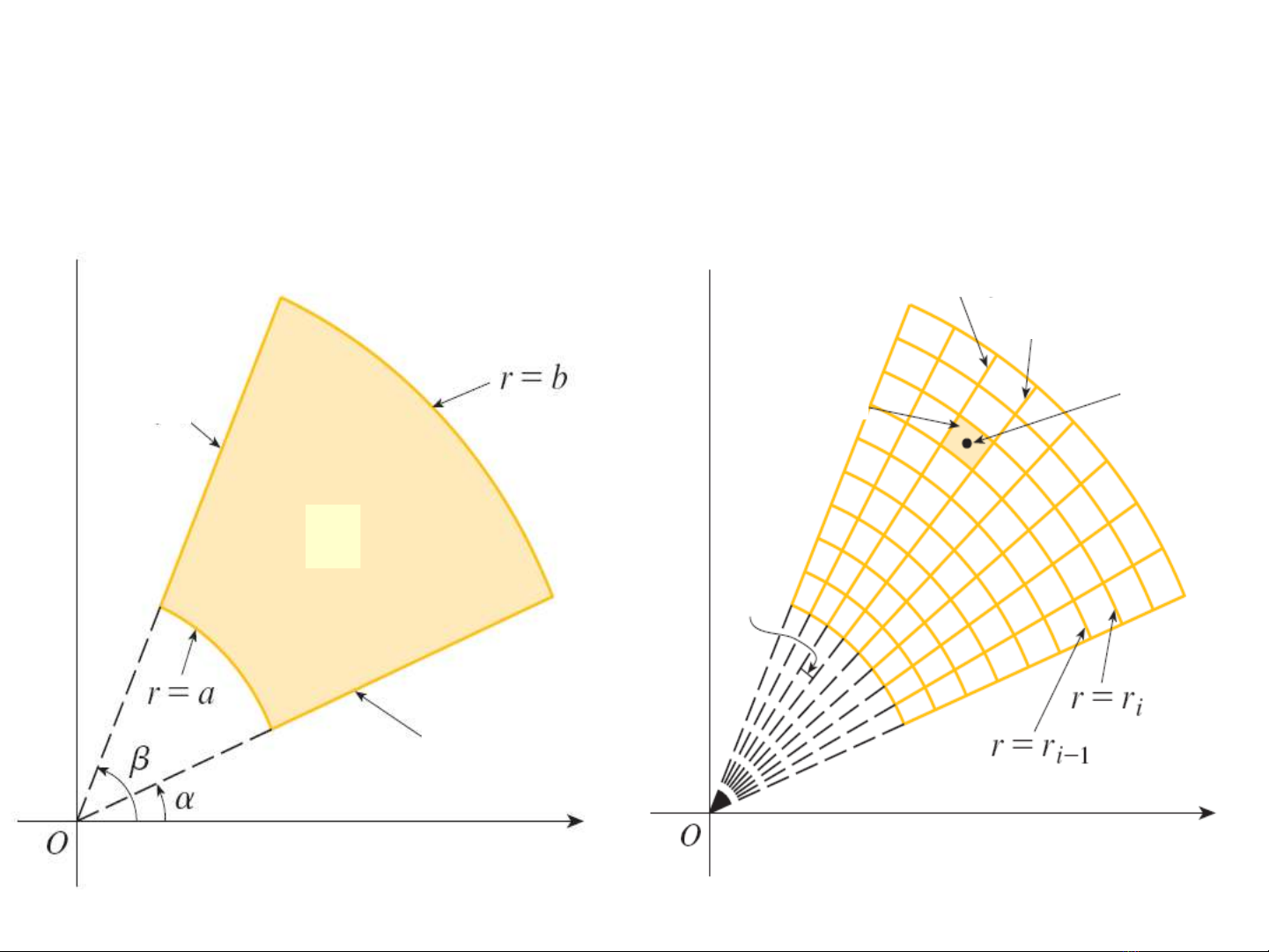
TÍCH PHÂN KÉP TRONG TỌA ĐỘ CỰC
D
ϕ α
=
ϕ β
=Dij
j
ϕ
1j
ϕ
−
( )
* *
,
i j
r
ϕ
ϕ
∆
:a r b
D
α ϕ β
Tổng tích phân
* * * * *
,
( cos , sin )
n i j i j i
i j
S f r r r r= ∆ ∆
ϕ ϕ ϕ
0
( , ) lim
n
d
D
f x y dxdy S
=
��
0
lim ( cos , sin )
n
dD
S f r r rdrd
=��
ϕ ϕ ϕ
Công thức đổi biến sang tọa độ cực
( , ) ( cos , sin )
D D
dxdy drdrf x y f r r=
��� ��
ϕϕϕ
cos , sin x r y
ϕ ϕ
= =