1
Chương 9. PHƯƠNG TRÌNH VI PHÂN
NỘI DUNG:
9.1. Phương trình vi phân cấp 1
9.2. Phương trình vi phân cấp 2
Phương trình vi phân là phương trình chứa hàm số
cần tìm, đạo hàm các cấp của nó và các biến số độc lập.
Lý thuyết phương trình vi phân xuất hiện từ cuối thế kỷ
17 do những đòi hỏi của cơ học và các ngành khoa học
tự nhiên khác, cùng thời kỳ với phép tính tích phân và
phép tính vi phân.
Toán Cao Cấp - ThS. Lê Trường Giang
2
Chương 9. PHƯƠNG TRÌNH VI PHÂN
Các phương trình vi phân đơn giản nhất xuất hiện
trong các công trình của nhà bác học Anh I. Newton và
nhà bác học Đức G. Leibniz; thuật ngữ “phương trình vi
phân” thuộc về G. Leibniz (1676, xuất bản năm 1684).
I. Newton khi sáng lập ra phép tính vi phân và tích phân
đã đặt ra hai bài toán, từ mối liên hệ giữa các hàm số
hãy xác định mối liên hệ giữa các đạo hàm; từ phương
trình chứa đạo hàm tìm mối liên hệ giữa các hàm số.
Theo quan điểm hiện nay, bài toán thứ nhất (tính
đạo hàm khi biết hàm số) thuộc phép tính vi phân, bài
toán thứ hai là nội dung của lý thuyết phương trình vi
phân thường.
Toán Cao Cấp - ThS. Lê Trường Giang
3
Chương 9. PHƯƠNG TRÌNH VI PHÂN
Bài toán tìm tích phân bất định F(x) của hàm số
f(x) được I. Newton xem là trường hợp riêng của bài
toán thứ hai. Quan điểm này của Newton đã được toán
học minh chứng: trong rất nhiều trường hợp các quy
luật thiên nhiên được mô tả dưới dạng phương trình vi
phân và đưa đến đòi hỏi phải giải những phương trình
này.
Đối với hàm hai biến thì phương trình vi phân là
phương trình chứa mối liên hệ giữa hai biến x,y và các
đạo hàm của y. Cấp của phương trình vi phân là cấp cao
nhất của đạo hàm của y xuất hiện trong phương trình.
Toán Cao Cấp - ThS. Lê Trường Giang
4
Chương 9. PHƯƠNG TRÌNH VI PHÂN
9.1. PHƯƠNG TRÌNH VI PHÂN CẤP 1
Phương trình vi phân cấp 1 là phương trình mà
đối đối tượng phải tìm là hàm số và hàm số phải tìm có
mặt trong phương trình dưới dấu đạo hàm hoặc vi phân
cấp 1.
Dạng phương trình:
Nghiệm tổng quát – nghiệm riêng
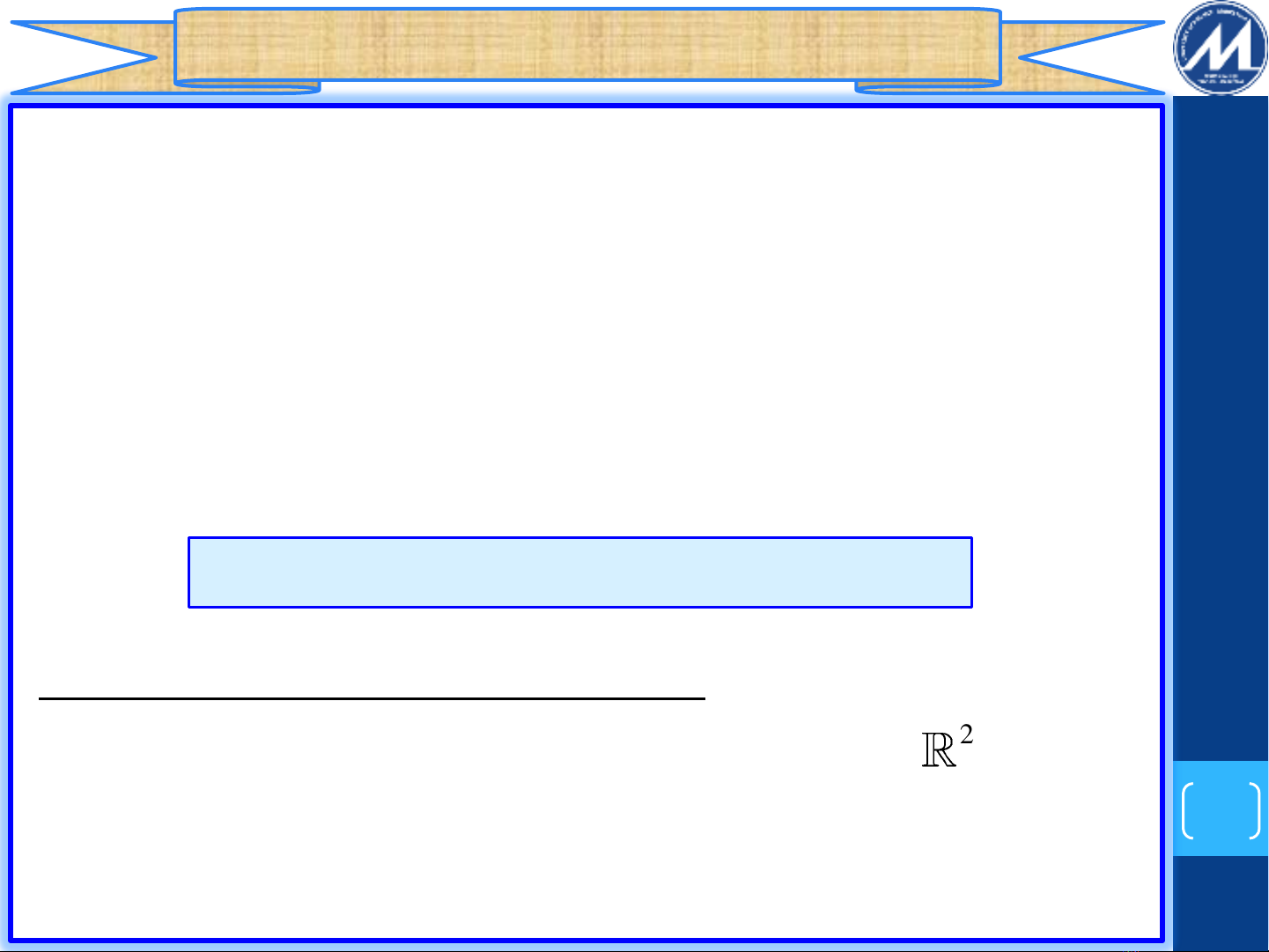
+ Nghiệm tổng quát của (1) trong miền là hàm
sao cho:
Toán Cao Cấp - ThS. Lê Trường Giang
5
F x, y, y 0 hay y f x, y 1


2
D
y x,C