ĐÁP ÁN – THANG ĐIỂM
ĐỀ THI THỬ ĐẠI HỌC ĐỢT 1 THÁNG 05/2014
Môn: TOÁN
Câu
h n
p n
i m
1
1 1 i m
Với m=1 ta có hàm số
32
7 16 12y x x x
1. Tập xác định: R
2. Sự biến thiên:
a Giới hạn:
lim , lim
xx
yy
 
0.25
b Bảng biến thiên:
Bảng biến thiên:
x
-
2 8/3 +
y'
+ 0 - 0 +
y
0 +
-
-4/27
0.25
- Hàm số ồng biến trên
8
;2 ; ;
3

 


,hàm số nghịch biến trên
8
2; 3



.
- Hàm số ạt cực ại tại x = 2, yC = 0, ạt cực ti u tại x = 8/3, yCT = -4/27.
0.25
3. Đồ thị: ồ thị giao với trục tung tại 0; -12 , giao với trục hoành tại 2;
0),(3; 0 . Nhận i m uốn
72
;
3 27
I


làm tâm ối xứng
8
6
4
2
2
4
6
10
5
5
10
y =
x
3
7
∙
x
2
+ 16
∙
x
12
0.25
2 1 i m
Tìm m sao cho đồ thị hàm số (Cm) cắt trục hoành ....
Hoàng ộ giao i m của ồ thị hàm số và trục hoành là nghiệm của pt:
0.25
2
32
2
4 3 15 1 9 3 0 1
3
4 3 1 0 2
x m x m x m
x
f x x mx m
ồ thị hàm số cắt trục hoành tại 3 i m phân biệt khi pt 1 có 3 nghiệm
phân biệt.
t 1 có 3 nghiệm phân biệt khi pt 2 có 2 nghiệm phân biệt kh c 3.
2
1
1
' 4 3 1 0
4
30 10
9
m
mm m
f
m



.
0.25
Khi ó
3; ;
B A C
x x x
là nghiệm của pt 2 . Yêu c u bài to n tương ương
pt 2 có hai nghiệm
1 2 1 2
; : 2 6
B
x x x x x
.
0.25
Theo Vi-et ta có
12
3
4 4 6 2
x x m m m
thỏa mãn k
Vậy
3
2
m
0.25
2 2
i m
1 1 i m
Giải phương trình:
41 3 7
4cos os2 os4 os
2 4 2
x
x c x c x c
pt
22
1 3 7
1 cos 2 cos 2 2cos 2 1 cos
2 4 2
x
x x x
0.5
3
cos 2 cos 2
4
x
x
cos 2 1
3
cos 1
4
x
x
0.25
8x k k Z
Vậy phương trình có nghiệm
8x k k Z

0.25
2 1 i m
Giải hệ phương trình:
2
17 3 5 3 14 4 0
4 2 19 3 8
x x y y
x y x
iều kiên:
2 5; 4xy
0.5
17 3 5 3 14 4 0
2 3 5 5 2 3 4 4 1
x x y y
x x y y
Xét hàm số
2
(3 2)y f t t t
với
0;t
Ta có
2
' 9 2 0 0f t t t
nên hàm số y=f t ồng biến trên
0; 
.
3
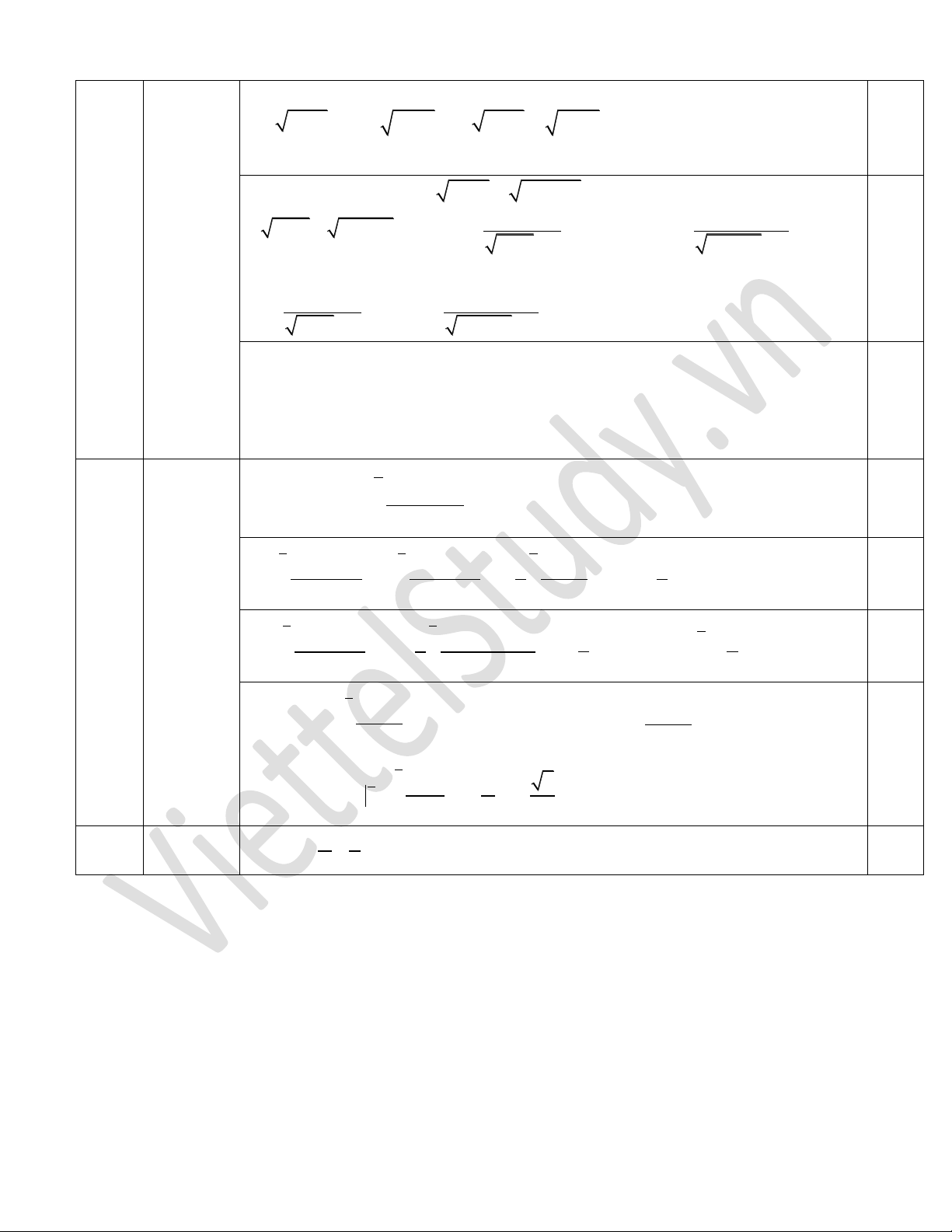
Ta thấy 1 có dạng
5 4 5 4 5 4
1
f x f y x y x y
yx
Thay vào pt(2) ta có:
2
4 2 22 3 8x x x
24( 2) 3( 2)
4 2 22 3 8 ( 2)( 2)
2 2 22 3 4
xx
x x x x x
xx

2
43
( 2) 0(*)
2 2 22 3 4
x
x
xx
0.25
Xét f(x)=VT(*) trên [-2;21/3],có f’ x >0 nên hàm số ồng biến. suy ra x=-
1 là nghiệm duy nhất của *
hương trình 2 có 2 nghiệm x=2 ; x=-1 nên hệ phương trình có 2 nghiệm
(2 ;1) ; (-1 ;-2 thỏa mãn iều kiện.
Vậy hệ phương trình có 2 nghiệm : (2 ;1) ; (-1 ;-2)
0.25
3
1 i m
T nh t ch phân
4
0
sin 2
1 os2
xx
dx
cx
4
0
sin 2
1 cos 2
xx
I dx
x
=
4
0
sin 2
1 cos 2
xdx
x
+
4
2
0
11
2 cos 2
xdx A J
x

0.25
Ta có A=
44
00
sin 2 1 (1 cos 2 )
1 cos 2 2 1 cos 2
x d x
dx
xx




4
0
11
ln(1 cos 2 ) ln 2
22
x



0.25
Tính
4
2
0cos
x
J dx
x
. ặt:
2
; tan
cos
dx
u x du dx dv v x
x
4
4
0
0
sin 2
( tan ) ln
cos 4 2
x
J x x dx
x
0.25
Vậy
1ln 2
84
I

0.25
4
4
1 i m
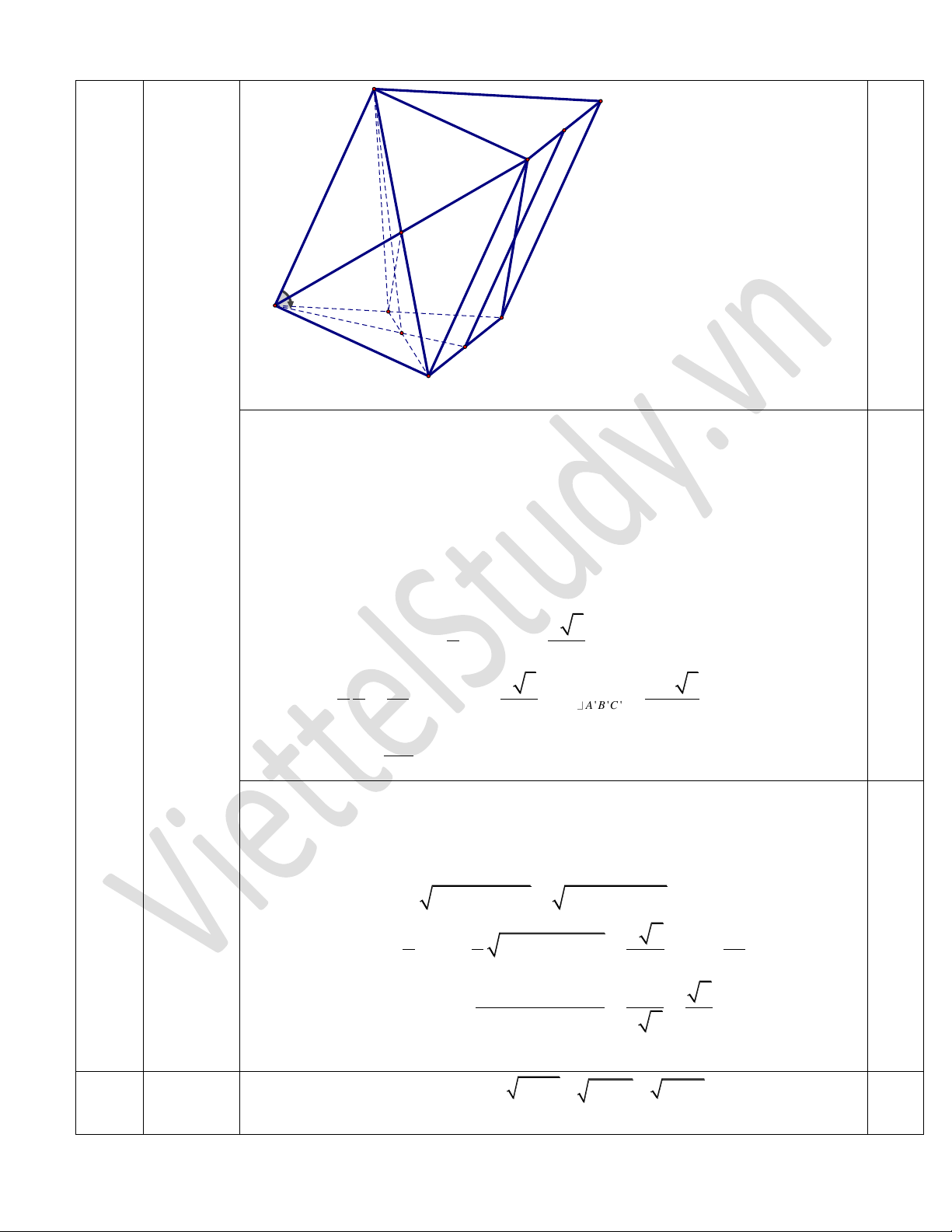
I
G
J
K
M
C'
B'
A
C
B
A'
*T nh th t ch khối l ng trụ:
0
00
2
' ' '
' ' ' ' '
ó ' ' ' ' ' AA ' ' '
à ' ' ' ' ' ' '
' ' ' ; ' ' ; ' ' ' , 60
ó ' ê ' 90 ê ' 60
3
à AA ' ê ' à
22
3 3 3 3 3
' ' '
2 2 4 2 16
A B C
lt
AG A B C AG B C
C A M B C B C G B C MK
m A B C BB C C B C
A B C BCC B ABC BCC B A M MK
Lai c AG GA n n AA G n n AA G
aa
M a n n A G v AG
a a a a
A M A B S
V

3
. ' ' '
9
32
ABC BA B C
a
0.5
*T nh góc giữa AB’ và BC’
Gọi I là giao i m của AB’ và A’B.J là trung i m A’C’ thì IJ song song
với BC’ nên
', ' ', IJAB BC AB
.
Xét tam gi c AJB’ có
2 2 2 2
22
2 2 2
0
' ' ' AA '
1 1 7 3
IJ ' ' ' ' ; '
2 2 4 4
IJ ' ' 1 7
cos ' 2 . ' 14
27
'; ' ';IJ 79
AB AG GB AG A G a
aa
BC BB B C JB
IB JB
JIB JI IB
AB BC AB

0.5
5
1 i m
Cho x,y, z kh ng âm thỏa mãn
2
1 1 2 1 2 5.x y z
Tìm gi trị lớn
nhất của bi u thức :
3 3 3
2P x y z
5
Ta có với hai số kh ng âm a, b ta có:
1 1 1 1a b a b
bình
phương hai vế lu n ng .
p dụng ta có:
2 2 2
2
2
5 1 1 2 1 2 1 1 2 . 1 2 2 1 2 2
2 2 8 4 2
x y z x y z x y z
x
x y z hay y z
Khi ó
3
2
3
33
2 2 4 2
x
P x y z x f x



0.5
Do x, y, z không âm nên
2
4 0 0;2 2
2
xx

dụng pp xét hàm số
22 0
3
' 2 12 2 16 0 2
4
x
f x x x x x x x
Vậy max =64 khi x=y=0 ;z=4 hoặc x=z=0 ; y=4
0.5
Câu
6a 2
i m
1)
1 i m
C có tâm I 1 ;2 b n k nh =2. Có
1 2 4
;2
2
d I d R

nên d và
C kh ng có i m chung. Vì vậy với mọi M thuộc d , qua M lu n k
ư c 2 tiếp tuyến tới C .
0.25
Có
2AMB AMI
nên góc AMB ạt gi trị lớn nhất khi
AMI
ạt gi trị
lớn nhất. Mà
AMI
là góc nhọn có
2
sin IA
AMI MI MI

,
AMI
ạt max khi
sin
AMI
ạt max khi MI ạt min. iều này xảy ra khi M là hình chiếu của
I trên (d).
0.25
Gọi H là hình chiếu của I trên d . Tìm H.
Lấy H thuộc d : y=-4-x nên H a ;-4-a . IH vu ng góc với d nên
.d
IH u
trong ó
d
u
là vecto ch phương của d .
Ta có
5 5 3
1; 6 ; 1; 1 . 0 ;
2 2 2
dd
IH a a u IH u t H 


0.25
Vậy M c n tìm là
53
;
22
M



0.25
2)
1 i m
Gọi pt mặt ph ng là:
2 2 2
00ax by cz d a b c
qua 2 i m C, D nên ta có hệ phương trình :
3 4 2 0
20
a b c d
a c d
0.25
4 4 0 : 2 0
22
a b a b P ax ay cz a c
d a c d a c



0.25