Đề kiểm tra - Ôn tập chương Toán 12 - Chương: Khảo sát hàm số (Đề số 19)

Chia sẻ: _ _ | Ngày: | Loại File: PDF | Số trang:14

Thêm vào BST

Báo xấu

5
lượt xem 1
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Đề kiểm tra - Ôn tập chương Toán 12 - Chương: Khảo sát hàm số (Đề số 19) là tài liệu luyện đề thiết thực dành cho học sinh lớp 12 đang trong quá trình ôn thi THPT. Bộ đề gồm 25 câu hỏi có đầy đủ lời giải, kèm theo chiến lược giải nhanh hiệu quả. Tài liệu hỗ trợ học sinh tiết kiệm thời gian trong phòng thi và tăng khả năng đạt điểm cao. Mời các bạn cùng tham khảo tài liệu để học tập tốt hơn.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Đề kiểm tra - Ôn tập chương Toán 12 - Chương: Khảo sát hàm số (Đề số 19)

ĐỀ SỐ 19 x3 2 Câu 1: Cho hàm số y = − 2 x 2 + 3x + . Toạ độ điểm cực đại của đồ thị hàm số là 3 3  2 A. ( −1;2) . B. (1; 2 ) . C. (1; − 2 ) . D.  3;  .  3 Câu 2: Hàm số y = f ( x ) có đạo hàm là f '( x) = x 2 ( x + 1)2 (2 x − 1) . Số điểm cực trị của hàm số là: A. 0. B. 1. C. 2. D. 3. x3 x 2 Câu 3: Hàm số y = + − 2 x − 1 đạt giá trị nhỏ nhất trên 0;2 là: 3 2 1 13 A. − . B. − . C. −1 . D. −4 . 3 6 Câu 4: Đường cong ở hình vẽ là đồ thị của một trong các hàm số dưới đây. Hàm số đó là hàm số nào? A. y = ( x − 1)( x + 2 ) . B. y = ( x − 1) ( x + 2 ) . 2 2 C. y = ( x − 1)( x − 2 ) . D. y = ( x + 1) ( x + 2 ) . 2 2 Câu 5: Tính giá trị cực tiểu yCT của hàm số y = x 4 − 2 x 2 + 3 . A. yCT = 2. B. yCT = −1. C. yCT = 3. D. yCT = 1. 2mx + 1 trên đoạn  2;3 là 5 Câu 6: Giá trị lớn nhất của hàm số y = khi m nhận giá trị bằng: m− x 4 A. −5 B. 1. C. −2 . D. −1. Câu 7: Các khoảng nghịch biến của hàm số y = x3 − 12 x + 12 là: A. ( −; −2 ) . B. ( −2;2) . C. ( −; −2) ; ( 2; +) . D. ( 2;+ ) . 1 Câu 8: Hàm số y = x3 + ( m + 1) x 2 − ( m + 1) x + 1 đồng biến trên tập xác định của nó khi: 3 A. −2  m  −1. B. −1  m  2 . C. −2  m  1. D. −2  m  −1 . Câu 9: Cho hàm số y = f ( x ) xác định, liên tục trên và có bảng biến thiên dưới đây:
Mệnh đề nào sau đây đúng? A. Hàm số đạt cực đại tại x = 1 . B. Hàm số có 2 điểm cực đại. C. Hàm số có 3 điểm cực trị. D. Hàm số nghịch biến trên khoảng ( −1;0 ) . x+3 Câu 10: Kí hiệu m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = trên đoạn 2x −1 1;4 . Tính giá trị biểu thức d = M − m . A. d = 4 . B. d = 5 . C. d = 2 . D. d = 3 . Câu 11: Hàm số y = x3 − 3x 2 + mx đạt cực tiểu tại x = 2 khi: A. m  0 . B. m  0 . C. m = 0 . D. m  0 . Câu 12: Một hàm số y = f ( x) = ax3 + bx 2 + cx + d , (a  0) có đồ thị như hình dưới đây Phương trình −5 = 2 f ( x) + 2m2 có bao nhiêu nghiệm? A. 2 . B. 1 . C. 0 . D. 3 . Câu 13: Hàm số y = 2 x 4 − 4 x 2 − 1 đồng biến trên những khoảng nào? A. ( −; −1) và ( 0;1) . B. ( −1;0 ) và (1;+ ) . C. ( −1;1) \ 0 . D. ( −; −1) và (1;+ ) . 3 − 2x Câu 14: Đồ thị hàm số y = có đường tiệm cận đúng, tiệm cận ngang là: x −1 A. x = 1; y = 2 . B. x = −1; y = −2 . C. x = 2; y = 1 . D. x = 1; y = −2 . Câu 15: Một hàm số y = ax3 + bx 2 + cx + d ,( a  0) có đồ thị như hình dưới đây
Chọn phát biểu đúng trong các phát biểu dưới đây? A. a  0,c  0 B. a  0,c  0 C. a  0,b  0,c  0 D. a  0,c  0 x +1 Câu 16: Phương trình tiếp tuyến của (C): y = tại giao điểm với trục hoành là: x −1 1 1 1 1 A. y = − ( x + 1) B. y = − ( x − 1) C. y = ( x − 1) D. y = ( x + 1) 2 2 2 2 Câu 17: Một ngọn hải đăng đặt ở vị trí A cách bờ 5km , trên bờ biển có một kho hàng ở vị trí C cách B một khoảng 7km . Người canh hải đăng có thể chèo thuyền từ A đến M trên bờ biển với vận tốc 4 km / h rồi đi bộ từ M đến C với vận tốc 6 km / h . Xác định độ dài đoạn BM để người đó đi từ A đến C nhanh nhất. 7 7 A. km . B. 2 5 km . C. 3 2 km . D. km . 2 3 Câu 18: Cho hàm số y = f ( x ) có đồ thị như hình vẽ. Tìm tất cả các giá trị của tham số m để phương trình f ( x ) = m − 2 có bốn nghiệm phân biệt. A. −2  m  −1 . B. −4  m  −3 . C. −4  m  −3 . D. −2  m  −1 .
Câu 19: Cho hàm số y = − x3 + 3x 2 − 2 có đồ thị ( C ) . Số tiếp tuyến với đồ thị ( C ) song song với đường thẳng y = −9 x − 7 là: A. 3 . B. 1 . C. 0 . D. 2 . Câu 20: Đồ thị hàm số y = − x 4 + x 2 + 2 cắt Oy tại điểm A. A ( 2;0 ) . B. O ( 0;0 ) . C. A ( 0; − 2 ) . D. A ( 0;2 ) . Câu 21: Cho hàm f ( x ) liên tục trên và hình dưới đây là đồ thị của hàm y = f  ( x ) Tìm các khoảng đồng biến của hàm y = f ( x ) ? A. ( − ; − 1) ; ( 3; +  ) B. ( −1;0) ; (1;3) C. ( −1;1) ; ( 3; +  ) D. ( − ;0) ; ( 3; +  ) Câu 22: Cho hàm số y = f ( x ) . Biết f ( x ) có đạo hàm f ' ( x ) và hàm số y = f  ( x ) có đồ thị như hình vẽ. Hàm số g ( x ) = f ( x − 1) đạt cực đại tại điểm nào dưới đây? A. x = 3. B. x = 2. C. x = 4 D. x = 1. Câu 23: Số giao điểm của đồ thị hàm số y = ( x 2 − 3x + 10 ) ( x + 3) và trục hoành là: A. 0 . B. 3 . C. 2 . D. 1 . 2x −1 Câu 24: Số đường tiệm cận của đồ thị hàm số y = là x2 + x + 2 A. 1 . B. 2 . C. 3 . D. 0 . Câu 25: Số giao điểm của hai đường cong y = x3 − x và y = x − x 2 là: A. 0. B. 2. C. 1. D. 3. BẢNG ĐÁP ÁN
1.B 2.B 3.B 4.B 5.A 6.D 7.B 8.A 9.C 10.D 11.C 12.B 13.B 14.D 15.A 16.A 17.B 18.A 19.D 20.D 21.C 22.A 23.D 24.B 25.D LỜI GIẢI CHI TIẾT x3 2 Câu 1. Cho hàm số y = − 2 x 2 + 3x + . Toạ độ điểm cực đại của đồ thị hàm số là 3 3  2 A. ( −1;2) . B. (1; 2 ) . C. (1; − 2 ) . D.  3;  .  3 Lời giải Chọn B Ta có y = x 2 − 4 x + 3. x = 1 y = 0   . x = 3 Bảng biến thiên: x − 1 3 + y + 0 − 0 + + 2 y 2 − 3 − Dựa vào bảng biến thiên ta thấy đồ thị hàm số đạt cực đại tại điểm (1; 2 ) . Câu 2. Hàm số y = f ( x ) có đạo hàm là f '( x) = x 2 ( x + 1)2 (2 x − 1) . Số điểm cực trị của hàm số là: A. 0. B. 1. C. 2. D. 3. Lời giải Chọn B   x=0  Cho f ' ( x ) = 0   x = −1 .  1 x=  2 Ta có bảng biến thiên: x 1 − −1 0 + 2 y' − 0 − 0 − 0 + 1 Dựa vào bảng biên thiên ta thấy f ' ( x ) chỉ đổi dấu 1 lần duy nhất khi đi qua điểm x = . 2
Vậy Hàm số y = f ( x ) có 1 cực trị. x3 x 2 Câu 3. Hàm số y = + − 2 x − 1 đạt giá trị nhỏ nhất trên 0;2 là: 3 2 1 13 A. − . B. − . C. −1 . D. −4 . 3 6 Lời giải Chọn B TXĐ: D = . x = 1 y = x 2 + x − 2 . y = 0  x 2 + x − 2 = 0   .  x = −2 Với x  0;2 , y = 0  x = 1 . 1 13 Ta có: y ( 0 ) = −1 ; y ( 2 ) = − ; y (1) = − . 3 6 13 So sánh các giá trị trên, ta được min y = y (1) = − . x0;2 6 Câu 4. Đường cong ở hình vẽ là đồ thị của một trong các hàm số dưới đây. Hàm số đó là hàm số nào? A. y = ( x − 1)( x + 2 ) . B. y = ( x − 1) ( x + 2 ) . 2 2 C. y = ( x − 1)( x − 2 ) . D. y = ( x + 1) ( x + 2 ) . 2 2 Lời giải Chọn B Đồ thị hàm số đi qua điểm ( 0; 2 )  Loại A, C. Đồ thị hàm số đi qua điểm (1;0 )  Loại D. Vậy, B đúng. Câu 5. Tính giá trị cực tiểu yCT của hàm số y = x 4 − 2 x 2 + 3 . A. yCT = 2. B. yCT = −1. C. yCT = 3. D. yCT = 1. Lời giải Chọn A
 x = −1 Xét phương trình y = 0  4 x3 − 4 x = 0   x = 0 .  x = 1  Lập bảng biến thiên của hàm số: x − hàm số là yCT = 2. Từ bảng biến thiên, giá− cực tiểu của1 trị 0 1 + y – 0 + 0 – 0 + 2mx + 1 trên đoạn 3  là 5 Câu 6. + Giá trị lớn nhất của hàm số y = 2;3 + khi m nhận giá trị bằng: y m− x 4 A. −5 B. 1. 2 C. −2 . 2 D. −1. Lời giải Chọn D 2m 2 + 1 Ta có y =  0 với x  m. (m − x) 2  Hàm số đồng biến trên từng khoảng xác định. TH1. Nếu m   2;3 . Hàm số có bảng biến thiên như sau: x − 2 m 3 +  Hàm số không tồn tại giá trị lớn nhất trên  2;3 . y + + + 6m + 1 –2m TH2. Nếu m   2;3  max y = y ( 3) = y 2;3 . m−3 –2m − 6m + 1 5 Giả thiết bài toán  =  m = −1. m−3 4 Câu 7. Các khoảng nghịch biến của hàm số y = x3 − 12 x + 12 là: A. ( −; −2 ) . B. ( −2;2) . C. ( −; −2) ; ( 2; +) . D. ( 2;+ ) . Lời giải Chọn B x = 2 Ta có y = 3x 2 − 12 = 0   .  x = −2 y  0 với mọi x  ( −2;2 ) nên hàm số nghịch biến trên khoảng ( −2;2) . Vậy hàm số nghịch biến trên khoảng ( −2;2 ) . 1 Câu 8. Hàm số y = x3 + ( m + 1) x 2 − ( m + 1) x + 1 đồng biến trên tập xác định của nó khi: 3 A. −2  m  −1. B. −1  m  2 . C. −2  m  1. D. −2  m  −1 . Lời giải Chọn A Tập xác định . Ta có y = x2 + 2 ( m + 1) x − ( m + 1) . Hàm số đồng biến trên tập xác định của nó khi y '  0 với mọi x  hay y = x2 + 2 ( m + 1) x − ( m + 1)  0 (1) với mọi x  . Ta có  = ( m + 1) . ( m + 2) khi đó (1)    0  ( m + 1) . ( m + 2)  0  −2  m  −1. Vậy −2  m  −1.
Câu 9. Cho hàm số y = f ( x ) xác định, liên tục trên và có bảng biến thiên dưới đây: x –∞ -1 0 1 +∞ Mệnh đề nào sau đây y' – 0 + 0 – 0 + đúng? A. Hàm +∞ -3 +∞ số đạt cực đại tại y x =1. B. Hàm số có 2 điểm cực đại. C. Hàm số có 3 điểm cực trị. D. -4 -4 Lời giải Chọn C Dựa vào bảng biến thiên ta thấy: +Hàm số đạt cực đại tại x = 0 nên đáp án A sai. +Hàm số có 3 điểm trị nên đáp án B sai, đáp án C đúng +Hàm số nghịc biến trên ( −; −1) và ( 0;1) nên đáp án D sai. x+3 Câu 10. Kí hiệu m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = trên đoạn 2x −1 1;4 . Tính giá trị biểu thức d = M − m . A. d = 4 . B. d = 5 . C. d = 2 . D. d = 3 . Lời giải Chọn D x+3 1  −7 Ta có tập xác định của hàm số y = là D = \   và y = . y  0 x  D 2x −1 2 ( 2 x − 1) 2  1 1  Từ đó ta có hàm số luôn nghịch biến trên  −;  và  ; +  suy ra hàm số luôn nghịch biến  2 2  trên 1;4 . Ta có M = y (1) = 4 , m = y ( 4) = 1 do đó d = M − m = 4 − 1 = 3 . Câu 11. Hàm số y = x3 − 3x 2 + mx đạt cực tiểu tại x = 2 khi: A. m  0 . B. m  0 . C. m = 0 . D. m  0 . Lời giải Chọn C Ta có, y = 3x 2 − 6 x + m . + Hàm số đạt cực tiểu tại x = 2  y(2) = 0  y(2) = 3.22 − 6.2 + m = 0  m = 0 . x = 0  y = 0 + Với m = 0  y = 3x 2 − 6 x = 3x( x − 2) , y = 0   .  x = 2  y = −4 Bảng biến thiên:
Từ bảng biến thiên ta thấy, hàm số đạt cực tiểu tại x = 2. Vậy, m = 0 hàm số y = x3 − 3x 2 + mx đạt cực tiểu tại x = 2. Câu 12. Một hàm số y = f ( x) = ax3 + bx 2 + cx + d , (a  0) có đồ thị như hình dưới đây Phương trình −5 = 2 f ( x) + 2m2 có bao nhiêu nghiệm? A. 2 . B. 1 . C. 0 . D. 3 . Lời giải Chọn B 5 Ta có, −5 = 2 f ( x) + 2m2  f ( x) = − − m2 . 2 5 5 5 Mà: − − m2  − , m  f ( x)  − , m . 2 2 2 Câu 13. Hàm số y = 2 x 4 − 4 x 2 − 1 đồng biến trên những khoảng nào? A. ( −; −1) và ( 0;1) . B. ( −1;0 ) và (1;+ ) . C. ( −1;1) \ 0 . D. ( −; −1) và (1;+ ) . Lời giải Chọn B x = 0 y = 8 x3 − 8 x ; y = 0    x = 1 Bảng biến thiên x − −1 0 1 + y − 0 + 0 − 0 + + −1 + y −5 −5 Hàm số y = 2 x 4 − 4 x 2 − 1 đồng biến trên khoảng ( −1;0 ) và (1;+ ) . 3 − 2x Câu 14. Đồ thị hàm số y = có đường tiệm cận đúng, tiệm cận ngang là: x −1 A. x = 1; y = 2 . B. x = −1; y = −2 . C. x = 2; y = 1 . D. x = 1; y = −2 . Lời giải Chọn D
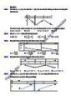
Tập xác định D = \ 1 3 −2 3 − 2x x lim y = lim = lim = −2  đường thẳng y = −2 là tiệm cận ngang của đồ thị hàm x → x → x − 1 x → 1 1− x số. Câu 15. Một hàm số y = ax3 + bx 2 + cx + d ,( a  0) có đồ thị như hình dưới đây Chọn phát biểu đúng trong các phát biểu dưới đây? A. a  0,c  0 B. a  0,c  0 C. a  0,b  0,c  0 D. a  0,c  0 Lời giải Chọn A Dựa vào đồ thị ta có: Khoảng ngoài cùng của đồ thi là đi lên cho nên a  0. Đồ thị có 2 điểm cực trị nằm về 2 phía trục Oy cho nên phương trình y = 0 có 2 nghiệm phân biệt trái dấu, tức là a.c  0 mà a  0 nên c  0 . x +1 Câu 16. Phương trình tiếp tuyến của (C): y = tại giao điểm với trục hoành là: x −1 1 1 1 1 A. y = − ( x + 1) B. y = − ( x − 1) C. y = ( x − 1) D. y = ( x + 1) 2 2 2 2 Lời giải Chọn A Giao điểm của đồ thi (C) với trục hoành là A ( −1; 0) . x +1 Phương trình tiếp tuyến của (C): y = f ( x ) = có dạng x −1 1 y = f  ( −1) .( x + 1) + 0 = − ( x + 1) . 2 Câu 17. Một ngọn hải đăng đặt ở vị trí A cách bờ 5km , trên bờ biển có một kho hàng ở vị trí C cách B một khoảng 7km . Người canh hải đăng có thể chèo thuyền từ A đến M trên bờ biển với vận tốc 4 km / h rồi đi bộ từ M đến C với vận tốc 6 km / h . Xác định độ dài đoạn BM để người đó đi từ A đến C nhanh nhất.
7 7 A. km . B. 2 5 km . C. 3 2 km . D. km . 2 3 Lời giải Chọn B Đặt BM = x ( km ) ,0  x  7 .  AM = 25 + x 2  Khi đó  CM = 7 − x  25 + x 2 7 − x  Thời gian người đó đi từ A đến C là: T = + . 4 6 25 + x 2 7 − x Xét hàm số f ( x ) = + trên đoạn 0 ; 7  .   4 6 f ( x) = x 1 − 4 25 + x 2 6 f  ( x ) = 0  6x − 4 25 + x2 = 0  x = 2 5 . Ta có: f ( 0 ) = 29 12 ; f (7 ) = 74 4 ( ) ; f 2 5 = 5 5 + 14 12 5 5 + 14  min f ( x ) = x=2 5. x0;7    12 Vậy người đó đi từ A đến C nhanh nhất khi BM = 2 5 . Câu 18. Cho hàm số y = f ( x ) có đồ thị như hình vẽ. Tìm tất cả các giá trị của tham số m để phương trình f ( x ) = m − 2 có bốn nghiệm phân biệt.
A. −2  m  −1 . B. −4  m  −3 . C. −4  m  −3 . D. −2  m  −1 . Lời giải Chọn A Ta có f ( x ) = m − 2 là phương trình hoành độ giao điểm của đồ thị hàm số y = f ( x ) và đường thẳng y = m − 2 .  Phương trình f ( x ) = m − 2 có bốn nghiệm phân biệt khi và chỉ khi đồ thị hàm số y = f ( x ) và đường thẳng y = m − 2 có bốn giao điểm  −4  m − 2  −3  −2  m  −1 . Câu 19. Cho hàm số y = − x3 + 3x 2 − 2 có đồ thị ( C ) . Số tiếp tuyến với đồ thị ( C ) song song với đường thẳng y = −9 x − 7 là: A. 3 . B. 1 . C. 0 . D. 2 . Lời giải Chọn D Hệ số góc k đường thẳng y = −9 x − 7 là k = −9 . Vì tiếp tuyến với đồ thị ( C ) song song với đường thẳng y = −9 x − 7 nên hệ số góc của tiếp tuyến là k = −9 . Ta có: y = −3x 2 + 6 x .  xo = −1 Gọi xo là hoành độ tiếp điểm, y ( xo ) = −9  −3xo 2 + 6 x = −9   .  xo = 3 Vậy có 2 tiếp tuyến với đồ thị ( C ) song song với đường thẳng y = −9 x − 7 . Câu 20. Đồ thị hàm số y = − x 4 + x 2 + 2 cắt Oy tại điểm A. A ( 2;0 ) . B. O ( 0;0 ) . C. A ( 0; − 2 ) . D. A ( 0;2 ) . Lời giải Chọn D Đồ thị hàm số y = − x 4 + x 2 + 2 với trục Oy tại điểm có hoành độ x = 0  y = 2 . Vậy đồ thị hàm số y = − x 4 + x 2 + 2 cắt Oy tại điểm A ( 0;2 ) .
Câu 21. Cho hàm f ( x ) liên tục trên và hình dưới đây là đồ thị của hàm y = f  ( x ) Tìm các khoảng đồng biến của hàm y = f ( x ) ? A. ( − ; − 1) ; ( 3; +  ) B. ( −1;0) ; (1;3) C. ( −1;1) ; ( 3; +  ) D. ( − ;0) ; ( 3; +  ) Lời giải Chọn C Từ đồ thị hình vẽ ta được ta được bảng xét dấu x − −1 1 3 + f ( x) − 0 + 0 − 0 + Kết luận: hàm số đồng biến tại ( −1;1) ; ( 3; +  ) . Câu 22. Cho hàm số y = f ( x ) . Biết f ( x ) có đạo hàm f ' ( x ) và hàm số y = f  ( x ) có đồ thị như hình vẽ. Hàm số g ( x ) = f ( x − 1) đạt cực đại tại điểm nào dưới đây? A. x = 3. B. x = 2. C. x = 4 D. x = 1. Lời giải Chọn C Từ đồ thị hình vẽ ta được bảng xét dấu f ( x ) x − 1 3 5 + g ( x) − 0 + 0 − 0 + Ta có g ( x ) = f ( x − 1) lúc này hàm số g ( x ) là hàm số f ( x ) dịch chuyển sang phải 1 đơn vị. Ta được bảng xét dấu g ( x ) x − 2 4 6 + g ( x) − 0 + 0 − 0 + Vậy hàm số g ( x ) đạt cực đại tại x = 3. Câu 23. Số giao điểm của đồ thị hàm số y = ( x 2 − 3x + 10 ) ( x + 3) và trục hoành là: A. 0 . B. 3 . C. 2 . D. 1 . Lời giải Chọn D x + 3 = 0 Phương trình hoành độ giao điểm: ( x 2 − 3x + 10 ) ( x + 3) = 0   2 .  x − 3x + 10 = 0
* x + 3 = 0  x = −3 . * x2 − 3x + 10 = 0 (vô nghiệm). Vậy đồ thị hàm số y = ( x 2 − 3x + 10 ) ( x + 3) cắt trục hoành tại 1 điểm. 2x −1 Câu 24. Số đường tiệm cận của đồ thị hàm số y = là x2 + x + 2 A. 1 . B. 2 . C. 3 . D. 0 . Lời giải Chọn B Ta có x2 + x + 2  0 x  nên hàm số xác định và liên tục trên . + Đồ thị hàm số không có tiệm cận đứng.  1 1 x2 −  2− 2x −1  x x + lim = lim = lim = 2 nên y = 2 là tiệm cận ngang. x →+ x +x+2 2 x →+ 1 2 x 1+ + 2 x →+ 1 2 1+ + 2 x x x x  1 1 x2 −  2− 2x −1  x x + lim = lim = lim = −2 nên y = −2 là tiệm cận x →− x +x+2 2 x →− 1 2 −x 1+ + 2 x →+ 1 2 − 1+ + 2 x x x x ngang. Vậy đồ thị hàm số đã cho có 2 đường tiệm cận. Câu 25. Số giao điểm của hai đường cong y = x3 − x và y = x − x 2 là: A. 0. B. 2. C. 1. D. 3. Lời giải Chọn D Số giao điểm của hai đường cong y = x3 − x và y = x − x 2 bằng số nghiệm của phương trình: x = 0  2 3 2 ( 2 ) x − x = x − x  x + x − 2x = 0  x x + x − 2 = 0  x = 1 . 3  x = −2  Vậy số giao điểm của hai đường cong y = x3 − x và y = x − x 2 là 3.