S GD – ĐT BÀ R A – VŨNG TÀUỞ Ị
Đ s 5ề ố
Đ THI H C KÌ 1 – Năm h c Ề Ọ ọ 2010 – 2011
Môn TOÁN L p 11ớ
Th i gian làm bài 90 phútờ
I. Ph n chung: (8 đi m)ầ ể
Câu I: (2,5 đi mể) Gi i các ph ng trình sau:ả ươ
1)
x2cos 1 0
− =
.
2)
x x3sin cos 3− =
3)
x x x x
2 2
3sin 4sin .cos 3cos 2+ − =
Câu II: (1,5 đi mể)
1) T các s 1, 2, 3, 4, 5 l p đ c bao nhiêu s t nhiên có 3 ch s khác nhau.ừ ố ậ ượ ố ự ữ ố
2) Ch n ng u nhiên 5 h c sinh t m t t g m 6 nam và 5 n . Tính xác su t sao cho có đúng 2 h cọ ẫ ọ ừ ộ ổ ồ ữ ấ ọ
sinh nam.
Câu III: (1đi mể) Trong m t ph ng t a đ Oặ ẳ ọ ộ xy, cho đ ng th ng d: ườ ẳ x – y + 3 = 0 và đi m I(1; 2). Tìmể
ph ng trình đ ng th ng dươ ườ ẳ 1 là nh c a d qua phép đ i x ng tâm I. ả ủ ố ứ
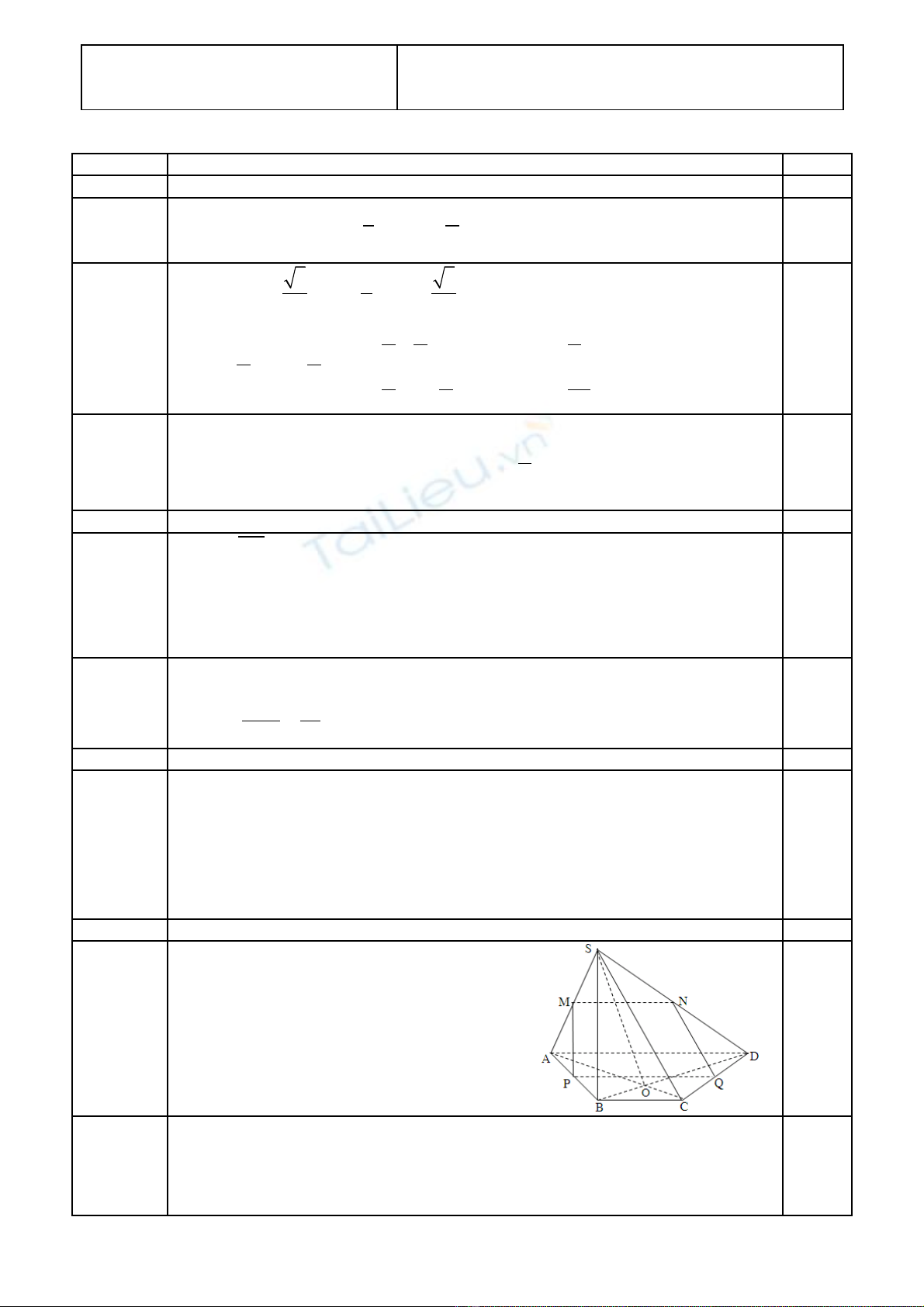
Câu IV: (2đi mể) Cho hình chóp S.ABCD có đáy ABCD là hình thang (c nh đáy l n AD). ạ ớ
1) Xác đ nh giao tuy n hai m t ph ng (SAC) và (SBD).ị ế ặ ẳ
2) G i M, N, P l n l t là trung đi m c a SA, SD và AB. Ch ng minh r ng: MN song song v iọ ầ ượ ể ủ ứ ằ ớ
m t ph ng (SBC). Xác đ nh thi t di n c a hình chóp S.ABCD c t b i m t ph ng (MNP). ặ ẳ ị ế ệ ủ ắ ở ặ ẳ
Câu V: (1đi mể) Gi i ph ng trình: ả ươ
x x x x x x
10 10 4 4 12 12
sin cos 2(cos sin ) 2(sin cos ).+ = − + +
II. Ph n riêng: ầ(2 đi mể) Thí sinh ch đ c ch n m t trong 2 ph n A ho c Bỉ ượ ọ ộ ầ ặ
Ph n Aầ
Câu VIa: (2đi mể)
1) Cho dãy s (uốn) v i ớ
n
n
un
2 1
2
+
=+
. Ch ng minh r ng dãy s (uứ ằ ố n) tăng và b ch n.ị ặ
2) Tìm giá tr l n nh t và giá tr nh nh t c a hàm s : ị ớ ấ ị ỏ ấ ủ ố
y x x x
2
2sin 2 2 3sin2 .cos2 2= + −
Ph n Bầ
Câu VIb: (2đi mể)
1) Tìm h s c a ệ ố ủ x10 trong khai tri n: ể
x2 8
( 2)−
.
2) Tìm m đ ph ng trình ể ươ
có nghi m ệ
x;
2
ππ
� �
� �
� �
.
--------------------H t-------------------ế
H và tên thí sinhọ: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . SBD :. . . . . . . . . .
1
S GD – ĐT BÀ R A – VŨNG TÀUỞ Ị
Đ s 5ề ố
ĐÁP ÁN Đ THI H C KÌ 1 – Năm h c Ề Ọ ọ 2010 – 2011
Môn TOÁN L p 11ớ
Th i gian làm bài 90 phútờ
Câu Đáp án Đi mể
Câu I 2,5
1)
(0,5 đ)
x x x k k Z
1
2cos 1 0 cos 2 ( )
2 3
ππ
− = = = +� � � �
0,25
0,25
2)
(1 đ) PT đã cho
x x
3 1 3
sin cos
2 2 2
− =� �
x k x k
x k Z
x k x k
2 2
6 3 2
sin sin ( )
5
6 3 2 2
6 3 6
π π π
π π
π π
π π π
π π π
� �
− = + = +
� �
� �
− = ���
� �
� �
� � � �
− = − + = +
� �
0,5
0,25
0,25
3)
(1 đ)
cosx = 0 không th a pt , chia 2 v c a pt cho cosỏ ế ủ 2x ta đ c pt:ượ
xx k
x x k Z
xx k
2tan 1
tan 4tan 5 0 ( )
4
tan 5 arctan( 5)
ππ
π
== +
+ − = ���
=−
= − +
0,25
0,25
0,25
Câu II 1,5
1)
(0,75 đ) G i ọ
x abc=
là s c n tìmố ầ
* S cách ch n c: 3 cách ố ọ
* S cách ch n a, b : ố ọ
A2
4
* V y có :3. ậ
A2
4
= 36 ( s )ố
0,25
0,25
0,25
2)
(0,75 đ) *
n C5
11
( )Ω =
*
n A C C
2 3
6 5
( ) .=
*
n A
P A n
( ) 25
( ) ( ) 77
= =
Ω
0,25
0,25
0,25
Câu III 1
(1 đ) * (d) đi qua M(0; 3), N(–3; 0)
* M1, N1 l n l t là nh c a M, N qua phép đ i x ng tâm I ầ ượ ả ủ ố ứ
suy ra M1(2; 1), N1(5; 4)
* (d1): x – y – 1= 0.
Ho c dùng bi u th c t a đ suy ra PT (ặ ể ứ ọ ộ
d1
), ho c ch c n m t đi m ặ ỉ ầ ộ ể
M1
r iồ
vi t PT (ế
d1)
đi qua
M1
và song song v i (d).ớ
0,25
0,5
0,25
Câu IV 2
1)
0,75 đ)
* V hình ẽ
* S là đi m chung th nh t c a (SAC),ể ứ ấ ủ
(SBD)
* G i O là giao đi m AC và BD suy ra O làọ ể
đi m chung th hai c a (SAC), (SBD) ể ứ ủ
SAC SBD SO( ) ( )=� �
0,25
0,25
0,25
2)
(1,25 đ) *
MN BC MN SBC
MN SBC
/ / / /( )
( )
* MN//(ABCD)
*
MNP ABCD PQ MN( ) ( ) =�
P
suy ra thi t di n là t giác MNQPế ệ ứ
0,5
0,25
0,25
0,25
2
Câu V 1
* PT
( ) ( ) ( )
x x x x x x
10 2 10 2 2 2
sin 1 2sin cos 1 2cos 2 cos sin− + − = −�
( )
x x x
10 10
cos2 sin cos 2 0− − =�
xx k k Z
x x
10 10
cos2 0 ( )
4 2
sin cos 2
π π
== +� � �
− =
(PT th 2 vô nghi m vì VTứ ệ
1 <
2
=VP )
0,25
0,25
0,25
0,25
Câu VIa 2
1)
(1 đ) *
n n
u u n n
13
( 2)( 3)
+− = + +
*
n n n n
u u n N u u n N
* *
1 1
0, ,
+ +
− > ∀ > ∀�� �
Suy ra (un) tăng
*
n
u n N
n
*
3
0 2 2,
2
< = − < ∀
+
Suy ra (un) b ch nị ặ
0,25
0,25
0,5
2)
(1 đ) *
y x x3sin4 cos4 1= − −
*
y x y x R2sin 4 1, 3 1,
6
π
� �
= − − − ∀
� �
� �
*
k k
y khi x k Z y khi x k Zmax 1 ( ) ,min 3 ( )
6 2 12 2
π π π π
= = + = − =− +� �
0,25
0,25
0,25
0,25
Câu VIb 2
1)
(1 đ) *
k k k k k k
k
T C x C x
2 8 16 2
1 8 8
( ) ( 2) ( 2)
− −
+= − = −
( k= 0,1,..,8 )
* H s c a ệ ố ủ x10 ng v i : 16– 2k = 10ứ ớ
k3=�
* V y h s c a ậ ệ ố ủ x10 là
C3 3
8( 2) 448− = −
025
0,25
0,25
0,25
2)
(1 đ) PT đã cho
x x m
2
2cos 3cos 2− + − =�
. Đ t t = cosặx, đk
t1;0
� �
−�
� �
Xét hàm s ố
f t t t t
2
( ) 2 3 2, 1;0
� �
= − + − −�
� �
L p BBT ậ
f f
min max
7; 2= − = −
. V y đ PT có nghi m thì ậ ể ệ
m7; 2
� �
− −�
� �
0,25
0,25
0,25
0,25
=====================
3