S GD & ĐT B C LIÊUỞ Ạ
Đ s 4ề ố
Đ THI H C KÌ 1 – Năm h c 2009 – 2010Ề Ọ ọ
Môn TOÁN L p 11ớ
Th i gian làm bài 90 phútờ
I. PH N B T BU CẦ Ắ Ộ (7 đi m)ể
Câu 1: (2 đi m) Tìm t p xác đ nh c a hàm s ể ậ ị ủ ố
x
yx
2 cos
1 cos
−
=+
.
Câu 2: (1 đi m) Gi i ph ng trình: ể ả ươ
x x x xcos5 3sin5 sin3 3cos3− − =
.
Câu 3: (1 đi m) Có 5 tem th khác nhau và 5 bì th khác nhau. H i có bao nhiêu cách dán tem vào bìể ư ư ỏ
th .ư
Câu 4: (1 đi m) Tìm to đ nh Mể ạ ộ ả ′ c a đi m M(4; 3) qua phép t nh ti n theo vect ủ ể ị ế ơ
v(2;1)=
r
.
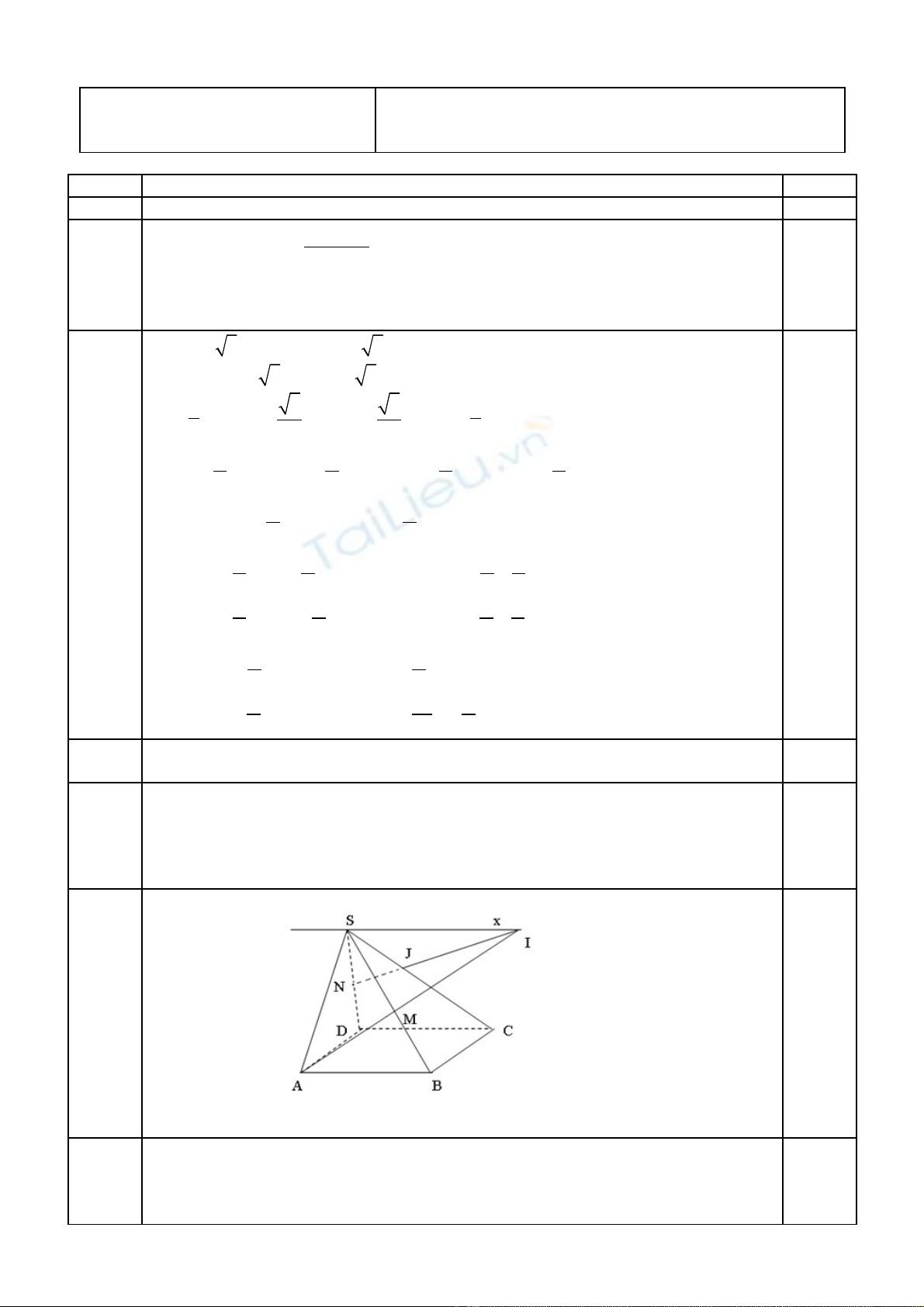
Câu 5: (2 đi m) Cho hình chóp S.ABCD có đáy ABCD là hình bình hành.ể
a) Xác đ nh giao tuy n c a hai m t ph ng (SAB) và (SDC).ị ế ủ ặ ẳ
b) G i M, N là trung đi m c a SB và SD. Tìm giao đi m c a đ ng th ng SC v i m t ph ngọ ể ủ ể ủ ườ ẳ ớ ặ ẳ
(AMN)
II. PH N T CH NẦ Ự Ọ (3 đi m)ể
A. Theo ch ng trình chu nươ ẩ
Câu 6a: (1 đi m) M t bàn dài có 6 gh đ c đánh s t 1 đ n 6. Ng i ta mu n x p 3 b n nam và 3ể ộ ế ượ ố ừ ế ườ ố ế ạ
b n n ng i vào bàn v i đi u ki n gh s 1 và gh s 2 ph i là 2 b n n . H i có bao nhiêu cáchạ ữ ồ ớ ề ệ ế ố ế ố ả ạ ữ ỏ
x p nh v y.ế ư ậ
Câu 7a: (1 đi m) M t đ n v v n t i có 10 xe ô tô, trong đó có 6 xe t t. H đi u đ ng m t cách nh uể ộ ơ ị ậ ả ố ọ ề ộ ộ ẫ
nhiên 3 xe đi công tác. Tính xác su t sao cho 3 xe đi u đ ng đi có ít nh t m t xe t t.ấ ề ộ ấ ộ ố
Câu 8a: (1 đi m) M t c p s c ng có 13 s h ng, s h ng đ u là 6, s h ng cu i là 42. Tìm t ng c aể ộ ấ ố ộ ố ạ ố ạ ầ ố ạ ố ổ ủ
t t c các s h ng c a c p s c ng đó.ấ ả ố ạ ủ ấ ố ộ
B. Theo ch ng trình nâng caoươ
Câu 6b: (1 đi m) Gi i ph ng trình:ể ả ươ
x x1 cos cos2 0
+ + =
.
Câu 7b: (1 đi m) Tìm t t c các s h ng h u t c a khai tri n ể ấ ả ố ạ ữ ỉ ủ ể
x
x
8
4
1
2
� �
+
� �
� �
, v i ớx là s h u tố ữ ỉ
d ng.ươ
Câu 8b: (1 đi m) M t vé x s có 5 ch s . Khi quay s , n u vé b n mua trùng hoàn toàn v i k t quể ộ ổ ố ữ ố ố ế ạ ớ ế ả
(trúng 5 s ) thì b n trúng gi i đ c bi t. N u vé b n mua có 4 ch s trùng v i 4 ch s c a gi iố ạ ả ặ ệ ế ạ ữ ố ớ ữ ố ủ ả
đ c bi t (t c là sai m t s b t kì hàng nào c a gi i đ c bi t) thì b n trúng gi i an i. B n Bìnhặ ệ ứ ộ ố ở ấ ủ ả ặ ệ ạ ả ủ ạ
mua m t t m vé x s .ộ ấ ổ ố
a) Tính xác su t đ Bình trúng gi i đ c bi t.ấ ể ả ặ ệ
b) Tính xác su t đ Bình trúng gi i an i.ấ ể ả ủ
--------------------H t-------------------ế
H và tên thí sinhọ: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . SBD :. . . . . . . . . .
1
S GD & ĐT B C LIÊUỞ Ạ
Đ s 4ề ố
ĐÁP ÁN Đ THI H C KÌ 1 – Năm h c 2009 – 2010Ề Ọ ọ
Môn TOÁN L p 11ớ
Th i gian làm bài 90 phútờ
Câu N i dungộĐi mể
A. Ph n b t bu c:ầ ắ ộ ( 7 đi m)ể
1(2đ)
Hàm s ố
x
yx
2 cos
1 cos
−
=+
xác đ nh khi cosịx
– 1
V y t p xác đ nh c a hàm s : ậ ậ ị ủ ố
D=
ﾢ
\
{ }
k k(2 1) ,
π
+
ﾢ
0,5
1,0
0,5
2(1đ)
x x x xcos5 3sin5 sin3 3cos3− − =
cos5x –
3
sin5x =
3
cos3x + sin3x
1
2
cos5x –
3
2
sin5x =
3
2
cos3x +
1
2
sin3x
cos
3
π
cos5x – sin
3
π
sin5x = cos
6
π
cos3x + sin
6
π
sin3x
cos ( 5x +
3
π
) = cos ( 3x –
6
π
)
x x k
x x k
5 3 2
3 6
5 3 2
3 6
π π π
π π π
+ = − +
+ = − + +
x k
x k
2 2
3 6
8 2
3 6
π π π
π π π
= − − +
= − + +
x k
x k
2 2
2
8 2
6
ππ
ππ
= − +
= − +
x k
k
x k
4( )
48 4
ππ
π π
= − +
= − +
ﾢ
0,25
0,25
0,25
0,25
3(1đ) C đ nh 5 bì th . M i hoán v c a 5 tem th là m t cách dán ố ị ư ỗ ị ủ ư ộ
V y có: Pậ5 = 5! = 120 cách dán tem vào bì thư0,5
0,5
4(1đ)
Ta có
v
x x
T M M x y y y
' 2
( ) '( '; ') ' 1
= +
= = +
r
x
y
' 6
' 4
=
=
M’( 6; 4)
0,5
0,5
5a(1đ)
a) mp(SAB) và mp(SCD) có chung nhau đi m S ể
l i ch a AB//CD nên chúng c t nhau theo giao tuy n Sx // AB // CDạ ứ ắ ế
0,5
0,25
0,25
5b(1đ) b) AM
(SAB) mà AM không song song v i Sx nên AM c t Sx t i Iớ ắ ạ
NI
(SCD)
NI c t SC t i J ắ ạ
Ta có J
SC (1)
J
NI mà NI
(AMN)
J
(AMN) (2)
0,25
0,25
2
T (1) và (2) ừ
J = SC
(AMN)
V y giao đi m c a SC v i mp(AMN) là đi m Jậ ể ủ ớ ể 0,25
0,25
B. Ph n t ch n:ầ ự ọ ( 3 đi m)ể
6a(1đ)
X p 2 trong 3 b n n vào 2 gh đ u là m t ch nh h p ch p 2 c a 3ế ạ ữ ế ầ ộ ỉ ợ ậ ủ
V y có ậ
A2
33.2 6= =
cách x pế
Còn l i 4 b n đ c x p vào 4 gh còn l i m i cách x p là m t hoán v c a 4ạ ạ ượ ế ế ạ ỗ ế ộ ị ủ
ph n t còn l iầ ử ạ
V y có Pậ4 = 4! = 24 cách x pế
Theo qui t c nhân có: ắ
A P
2
3 4
. 6.24 144= =
cách x pế
0,5
0,25
0,25
7a(1đ)
Ta có: n(
Ω
) =
C3
10
= 120
G i A là bi n c 3 xe đi u đ ng đi công tác có ít nh t m t xe t tọ ế ố ề ộ ấ ộ ố
A
là bi n c 3 xe đi u đ ng đi công tác không có xe nào t tế ố ề ộ ố
n(
A
) =
C3
44=
n(A) = n(
Ω
) – n(
A
) = 120 – 4 = 116
P(A) =
n A
n
( ) 116 29
( ) 120 30
Ω
= =
0,25
0,25
0,25
0,25
8a(1đ)
Ta có:
( )
n
n
n u u
S1
2
+
=
( )
13 6 42 312
2
+
= =
0,5
0,5
6b(1đ)
1 + cosx + cos2x = 0
2cos2x + cosx = 0
cosx( 2cosx + 1) = 0
xx k
k
xx k
cos 0 2( )
12
cos 2
23
ππ
ππ
== +
� �
= −
= +
ﾢ
0,25
0,25
0,25
0,25
7b(1đ)
S h ng t ng quát c a khai tri n:ố ạ ổ ủ ể
( )
kk k k
k
k k k k k
k
T C x C x x C x
x
3
84 4
2 4 4
1 8 8 8
4
1
. .2 . 2 .
2
−− − −
− −
+
� �
= = =
� �
� �
k
T1+
là s h u t n u 3ố ữ ỉ ế k chia h t cho 4 vì ế
k0 8
nên k = 0, k = 4, k = 8
+ k = 0
T C x x
0 4 4
1 8
= =
+ k = 4
T C x C x x
4 4 4 3 4
5 8 8
1 35
2 . .
16 8
− −
= = =
+ k = 8
T C x
x x
8 8 2
9 8 8 2 2
1 1
.2 . 2 . 256.
− −
= = =
V y khai tri n trên có 3 s h ng s h u t là ậ ể ố ạ ố ữ ỉ x4 ,
x
35
8
,
x2
1
256
0,25
0,25
0,25
0,25
8b(1đ) a ) S k t qu có th là 10ố ế ả ể 5 = 100000
Ch có m t k t qu trùng v i s c a Bình . Do đó xác su t trúng gi i đ c bi tỉ ộ ế ả ớ ố ủ ấ ả ặ ệ
c a Bình là ủ
10,00001
100000 =
b) Gi s vé c a Bình là ả ử ủ
abcde
. Các k t qu trùng v i đúng b n ch s c aế ả ớ ố ữ ố ủ
Bình là
abcdt
(t
e) ho c ặ
abcte
(t
d) ho c ặ
abtde
(t
c) ho c ặ
atcde
(t
0,25
0,25
3
b) ho c ặ
tbcde
(t
a). V y có 9 + 9 + 9 + 9 + 9 = 45 k t qu đó vé Bình trúngậ ế ả ở
an iủ
Do đó xác su t trúng gi i an i c a Bình là ấ ả ủ ủ
45 0,00045
100000 =
0,25
0,25
======================
4